Задание 17. Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1 806 000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено в таблице.
— каждый январь долг возрастает на 15 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?
Обозначим начальную сумму долга S = 1806000 рублей.
При первом варианте сумма S сначала возрастает на 15% и становится равной 1,15S, а затем, делается выплата m рублей. Остается сумма долга:
Дифференцированный платеж #6 ЕГЭ №513106
которая на второй год также увеличивается на 15% и делаются такие же выплаты m рублей. После чего долг полностью гасится. Получаем уравнение:
В результате, Алексей должен выплатить по первому варианту
2∙1110900 = 2221800 рублей
При втором варианте выплаты происходят помесячно. Долг сначала возрастает на 2%, становится равным 1,02S, а затем, делаются выплаты так, чтобы долг равномерно уменьшался, то есть, в первый месяц нужно выплатить:
Аналогично для следующего месяца, только долг теперь будет составлять, получаем остаток долга в размере:
После 24 месяцев выплаты будут составлять сумму, равную
Перепишем эту сумму в виде:
Получаем первый более выгодный вариант на
22575000 – 2221800 = 35700 рублей
Ответ: 35700
Источник: self-edu.ru
Оценка эксперта: 3 балла.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
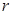
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
ЕГЭ Математика Задание №15#513106
Комментарий.
Почти правильное решение, содержащее ошибки (вычислительного характера). Две ошибки: 1) 
, а не 
; 2) 
, т.е. должно быть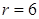 
– не позволяют выставить 2 балла.
Оценка эксперта: 1 балл.
Пример 4.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
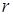
— каждый январь долг увеличивается на % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
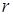
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите .
Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 3 балла.
Пример 5.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите .
Комментарий.
В решении без объяснений записаны уравнения. Переход от системы к уравнению относительно k не объяснен. Числовой ответ явно не получен: не извлечен корень из числа 14641. Таким образом, решение недостаточно обоснованное.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
О решении задач на кредиты и вклады. Платежи «По настроению»
Тренировочные задачи, предлагаемые обучающимся выпускных классов, не всегда связаны с периодическими дифференцированными или аннуитетными платежами клиента. Бывают такие, которые предполагают частично дифференцированные, частично аннуитетные формы платежей. Бывают даже такие, какие предполагают выплаты клиента, скажем, «по настроению».
Рассмотрим несколько и таких задач.
Начнем с задачи 17 варианта 10 Сборника под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова, ЕГЭ-2019, математика, профильный уровень, 40 тренировочных вариантов.
Задача 19.
Николай Сергеевич взял кредит 1 февраля 2015 года на сумму $$S$$млн рублей. Условия его возврата таковы:
— 1 марта года долг увеличивается на 10% по сравнению с началом года;
— с 1 мая по 1 августа необходимо выплатить часть долга;
— 1 марта каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Год | 2015 | 2016 | 2018 | 2018 | 2019 | 2020 | |||
| Долг (млн.руб) | S | S-1 | S-2 | S-2,4 | S-2,8 | S-3 | . | 0,2 | 0 |
(Начиная с 2020 года долг равномерно уменьшается на 200000 рублей в год).
В каком году Николай Сергеевич планирует совершить последний платеж, если общая сумма выплат равна 17680000 рублей?
1.Первый кредитный период с 2015-го по 2019-й год.
| Дата | Долг на начало кредитного года | Выплачено | Долг на конец кредитного года |
| 01.03.2015 | Scdot 1,1=1,1S$$ | $$1,1S-(S-1)=$$$$1,1S-S+1=$$$$0,1S+1$$ | $$S-1$$ |
| 01.03.2016 | $$(S-1)cdot 1,1=$$$$1,1S-1,1$$ | $$1,1S-1,1-S+2=$$$$0,1S+0,9$$ | $$S-2$$ |
| 01.03.2017 | $$(S-2)cdot 1,1=$$$$1,1S-2,2$$ | $$1,1S-2,2-S+2,4=$$$$0,1S+0,2$$ | $$S-2,4$$ |
| 01.03.2018 | $$(S-2,4)cdot 1,1=$$$$1,1S-2,64$$ | $$1,1S-2,64-S+2,8=$$$$0,1S+0,16$$ | $$S-2,8$$ |
| 01.03.2019 | $$(S-2,8)cdot 1,1=$$$$1,1S-3,08$$ | $$1,1S-3,08-S+3=$$$$0,1S-0,08$$ | $$S-3$$ |
Выплачено $$0,1S+1+0,1S+0,9+0,1S+0,2+$$$$+0,1S+0,16+0,1S-0,8=0,5S+2,18$$ (млн руб.)
Остаток долга клиента становится $$(S-3)$$ млн рублей. Обозначим его К. ($$S=K+3).$$
2. Второй кредитный период — до полного погашения кредита.
Пусть Николай Сергеевич с долгом в размере $$K$$ млн рублей расплачивался $$n$$ лет, начиная с 1 мая 2020 года.
Названные ежегодные выплаты состоят из двух частей:
первая часть неизменная, и она равна $$frac$$ млн рублей;
вторая часть, обусловленная процентными ставками банка, — переменная, из года в год уменьшаемая на одну и ту же сумму, равную $$0,02$$ млн рублей, образуя конечную арифметическую прогрессию $$(a_n)$$. В ней $$a_1=0,1K,$$ последний $$n-$$й член представляется формулой $$a_n=frac<0,1K>,$$ что равно 0,02. Откуда: $$0,1K=0,02n$$ или $$K=0,2n.$$
Из условия задачи и сказанного выше имеем: за $$n$$ лет второго кредитного периода банку было возвращено $$(К+S_1)$$ млн рублей, где $$S_1-$$сумма первых $$n$$ членов названной прогрессии.
Тогда $$S_ =$$$$fraccdot n=fraccdot n=0,01n^2+0,01n.$$ Это — с одной стороны. С другой же стороны, общая сумма, которую Николай Сергеевич выплатит банку во второй период, составляет:
$$17,68-0,5S-2,18=15,5-0,5S=15,5-$$ $$0,5(K+3)=14-0,5K,$$ из которой К — часть суммы основного долга. Это значит, что $$S_1=14-0,5K-K=$$$$14-1,5K=14-1,5cdot 0,2n=$$$$14-0,3n$$
Положительный корень уравнения равен 25.
Заметим, что первый год второго кредитного периода будет 2020 год, который находится путем прибавления 1 к последнему 2019 году первого кредитного года.
Коли это так, то искомое число равно $$2019+25=2044.$$
О т в е т: в 2044-м году.
А теперь рассмотрим задачи попроще.
Задача 20.
Индивидуальному предпринимателю 15 июня был выдан кредит на приобретение стройматериалов. В нижеследующей таблице указан график его погашения. Текущий долг указывается в процентах:
| Дата | 15.06 | 15.07 | 15.08 | 15.09 | 15.10 | 15.11 | 15.12 |
| Текущий долг | 100% | 85% | 65% | 40% | 30% | 20% | 0% |
В конце каждого месяца, начиная с июня, банк увеличивает текущий долг на 7%. После этого в первой половине последующего месяца индивидуальный предприниматель обязан внести в банк такую сумму, чтобы оставшийся долг стал равным указанному в таблице текущему долгу на 15 число этого месяца.
На сколько процентов общая сумма выплат при таких условиях больше суммы кредита?
Предположим, что клиенту выдан кредит в сумме у.е. Динамику погашения кредита покажем в таблице. (В у.е.)
| Месяц | Долг на начало месяца | Выплачено банку | Долг к концу месяца |
| Июль | $$1,07S$$ | $$(1,07-0,85)S=$$$$0,22S$$ | $$0,85S$$ |
| Август | $$0,85Scdot 1,07=$$$$0,9095S$$ | $$(0,9095-0,65)S=$$$$0,2595S$$ | $$0,65S$$ |
| Сентябрь | $$0,65Scdot 1,07=$$$$0,6955S$$ | $$(0,6955-0,4)S=$$$$0,2955S$$ | $$0,4S$$ |
| Октябрь | $$0,4Scdot 1,07=$$$$0,428S$$ | $$(0,428-0,3)S=$$$$0,128S$$ | $$0,3S$$ |
| Ноябрь | $$0,3Scdot 1,07=$$$$0,321S$$ | $$(0,321-0,2)S=$$$$0,121S$$ | $$0,2S$$ |
| Декабрь | $$0,2Scdot 1,07=$$$$0,214S$$ | $$0,214S$$ | $$0$$ |
| Общая сумма выплат банку | $$(0,22+0,2595+$$$$0,2955+0,128+$$$$0,121+0,214)S=$$$$1,238S$$ | ||
Общая сумма выплат больше суммы самого кредита на $$0,238S$$ у.е.
Искомое процентное отношение: $$0,238S:Scdot 100%=23,8%.$$
О т в е т: на 23,8 %.
Задача 21.
В мае 2016 года взяли кредит на $$S$$ млн рублей, где $$S$$ — целое число, на 5 лет.
Условия его возврата таковы:
— каждый ноябрь долг возрастает на 20% по сравнению с концом предыдущего года;
— с декабря по апрель каждого года необходимо выплатить часть долга;
— в мае каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Год | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| Долг (в млн руб.) | S | 0,7S | 0,5S | 0,4S | 0,2S | 0 |
Найдите наименьшее целое значение $$S$$, чтобы общая сумма выплат было больше 7 млн рублей.
Расчеты возврата долга покажем в следующей таблице (В млн руб.):
| Год кредитования | Долг на начало года кредитования | Выплата банку | Долг на конец кредитного года |
| 1 | $$1,2S$$ | $$(1,2-0,7)S=0,5S$$ | $$0,7S$$ |
| 2 | $$0,7Scdot 1,2$$$$=0,84S$$ | $$(0,84-0,5)S=0,34S$$ | $$0,5S$$ |
| 3 | $$0,5Scdot 1,2$$$$=0,6S$$ | $$(0,6-0,4)S=0,2S$$ | $$0,4S$$ |
| 4 | $$0,4Scdot 1,2$$$$=0,48S$$ | $$(0,48-0,2)S=0,28S$$ | $$0,2S$$ |
| 5 | $$0,2Scdot 1,2$$$$=0,24S$$ | $$0,24S$$ | 0 |
| Всего возвращено банку | $$(0,5+0,34+0,2+$$$$0,28+0,24)S=1,56S$$ | ||
Таким образом, банку подлежит возвращению всего $$1,56S$$ млн руб.
По условию задачи: $$1,56S>7$$. Это значит: $$S>4,487$$.
Последнему неравенству удовлетворяю целочисленные значения S: 5; 6; 7;. наименьшим из которых является число 5.
Задача 22.
В июле 2019 года планируется взять кредит в банке в размере N млн рублей, где N — натуральное число, сроком на 3 года.
Условия его возврата такова:
— каждый январь долг увеличивается на 20 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2019 | Июль 2020 | Июль 2021 | Июль 2022 |
| Долг (в млн руб.) | N | 0,6N | 0,4N | 0 |
Найдите наименьшее значение N, при котором каждая из выплат будет составлять целое число миллионов рублей.
Р е ш е н и е (В млн рублей):
| Год | Долг в январе | Долг в июле | Размер выплаты |
| 2019 | — | N | — |
| 2020 | $$1,2N$$ | $$0,6N$$ | $$1,2N-0,6N=0,6N$$ |
| 2021 | $$0,6Ncdot 1,2=0,72N$$ | $$0,4N$$ | $$0,72N-0,4N=0,32N$$ |
| 2022 | $$0,4Ncdot 1,2=0,48N$$ | 0 | $$0,48N$$ |
Таким образом, размеры выплат клиента в млн руб. составляют $$fracN ;frac;NfracN.$$ Все коэффициенты — несократимые дроби, для которых наименьшим общим знаменателем является 25. Отсюда: искомым значением N является число 25.
Задача 23.
Клиент планирует взять кредит на целое число миллионов рублей сроком на 5 лет. В середине каждого года действия кредита долг клиента возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го, 3-го годов клиент выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов клиент выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат клиента превысит 20 млн рублей.
Пусть К млн руб. — размер кредита, х млн руб. — размер выплаты клиента в 4-й и 5-й годы кредитования. Тогда (В млн рублей):
| Год кредитования | Долг к началу отчетного периода | Выплата | Долг к концу отчетного периода |
| 1 | $$1,2К$$ | $$0,2К$$ | $$K$$ |
| 2 | $$1,2К$$ | $$0,2К$$ | $$K$$ |
| 3 | $$1,2К$$ | $$0,2К$$ | $$K$$ |
| 4 | $$1,2К$$ | $$x$$ | $$1,2K-x$$ |
| 5 | $$(1,2К-х)cdot 1,2=$$$$1,44К-1,2х$$ | $$x$$ | $$1,44К-2,2х=0$$ |
Найдем х. $$1,44К-2,2х=0$$< >$$Leftrightarrow $$ $$х=frac$$ $$Leftrightarrow $$ $$х=frac.$$
Сумма выплат клиента за все годы кредитования составляет $$0,6K+2х=0,6K+fracK=$$$$fracK=fracK=fracK.$$
Известно: $$fracK>20Leftrightarrow $$ $$K>10,47. $$
Последнему неравенству удовлетворяют целочисленные значения К: 11; 12; 13;. наименьшим из которых является число 11.
О т в е т: 11 млн рублей.
Задача 24.
В начале месяца Василий взял в банке кредит 2,4 млн рублей с месячной процентной ставкой 5% на 12 месяцев с погашением кредита по следующей схеме:
— в начале каждого месяца банк увеличивает долг на 5%;
— выплаты производятся в конце каждого месяца;
— каждая следующая выплата на 5% больше предыдущей.
Сколько рублей должна составлять первая выплата, чтобы Василий погасил свой кредит по указанной схеме за 12 месяцев?
Пусть размер кредита составляет К рублей, процентная ставка банка увеличивает долг клиента в q раз, размер процентной ставки банка в первый месяц кредитования составляет х рублей. Тогда:
| Год кредитования | Долг клиента к началу очередного года кредитования | Выплата клиента | Долг клиента в конце очередного года кредитования |
| 1 | $$Кq$$ | $$x$$ | $$Kq-x$$ |
| 2 | $$(Kq-x)q=$$$$Kq^2-xq$$ | $$xq$$ | $$Kq^2-2xq$$ |
| 3 | $$(Kq^2-2xq)q=$$$$Kq^3-2xq^2$$ | $$xq^2$$ | $$Kq^3-3xq^2$$ |
| . | . | . | . |
| 12 | $$Kq^-12xq^$$ | $$xq^$$ | $$Kq^-12xq^=0$$ |
О т в е т: 210000.
Задача 25.
15 февраля планируется взять кредит в банке на сумму 2 млн рублей сроком 5 месяцев.
Условия его возврата такова:
— 1-го числа каждого месяца долг возрастет на целое число х % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца 1 мая по необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую часть взятого кредита в соответствии со следующей таблицей:
| Дата | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг |
Найдите наибольшее целое значение х, при котором общая сумма выплат будет составлять менее $$2,4$$млн руб.
Пусть $$К$$ — размер кредита (в млн. руб), q — коэффициент, который связывает процент банка по кредиту с соответствующим долгом клиента: $$q=1+0,01x$$. Тогда (В млн рублей):
| Месяцы | Долг на 1-е число | Частичная выплата клиента | Долг на 15-е число |
| Февраль | — | — | K |
| Март | $$Кq$$ | $$Кq-0,7K$$ | $$0,7K$$ |
| Апрель | $$0,7K$$ | $$0,7Кq-0,5K$$ | $$0,5K$$ |
| Май | $$0,5K$$ | $$0,5Кq-0,4K$$ | $$0,4K$$ |
| Июнь | $$0,4K$$ | $$0,4Кq-0,2K$$ | $$0,2K$$ |
| Июль | $$0,2K$$ | $$0,2K$$ | 0 |
| Общая сумма выплат | $$(1+0,7+0,5+0,4+0,2)Кq-$$$$(0,7+0,5+0,4+0,2)K$$$$=2,8Kq-1,8q$$ | ||
Если кто-то хочет знать больше, чем требуется строгим экспертам
Задача 25+1.
В июле планируется взять в кредит в банке на некоторую сумму. Условия его возврата таковы: 1) каждый январь долг возрастает на $$r%$$ по сравнению с концом предыдущего года; 2) с февраля по июнь каждого года необходимо выплатить некоторую часть долга. Найдите число $$r$$, если известно, что если каждый год выплачивать по 1464100 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 2674100 рублей, то кредит будет полностью погашен за 2 года.
Если ежегодная фиксированную сумму, подлежащую выплате банку обозначить , сумму кредита $$К$$, коэффициент, который каждый январь повышает долг клиента на $$r%,$$ m, срок, на который взят кредит, $$n$$, то:
Если кредит будет погашен за 4 года, то: $$frac=1464100$$ (1)
а если же он будет погашен за 2 года, то: $$frac=2674100$$ (2)
Найдем отношение левых и правых частей равенств (1) и (2).
Положительный корень последнего уравнения: $$m=1,1,$$ откуда: $$1+0,01r=1,1$$ $$Leftrightarrow $$ $$Leftrightarrow 0,01r=0,1$$ $$Leftrightarrow $$ $$r=10.$$
Источник: mathlesson.ru
