Постоянный пользователь нашего ресурса написал нам почту в 21:29 с просьбой предоставить развернутый ответ на его вопрос. Наши эксперты отнесли этот вопрос к разделу Разное. Для ответа был привлечен один из опытных специалистов, который занимается написанием студенческих работ.
Цитируем вопрос ваш вопрос
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
Разбор вопроса и ответ на него
Раздел ‘ЕГЭ (школьный)’, к которому был отнесён этот вопрос является не простой рубрикой. Для подготовки ответа на вопросы из этой рубрики специалист должен обладать широкими познаниями в различных научных областях. Однако в нашей компании таковые имеются.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
Конечно этот ответ может полностью не раскрыть тему вопроса, но мы постарались сделать его максимально полным. Предлагаем ознакомиться с мнением эксперта по этой теме:
ЕГЭ Математика Задание 15#513106
Пусть взяли в кредит a рублей (все суммы в рублях). По условиям задачи заполним в таблице суммы долга на 15-е число каждого месяца (второй столбец таблицы), увеличим на 5 % полученные суммы (третий столбец таблицы). Вычислим платежи каждого месяца, вычитая из числа в
3-м столбце таблицы число во 2-м столбце таблицы строкой ниже.
Источник: www.referat-web.ru
Тип: Нахождение ежегодного ( ежемесячного) транша.
Максим хочет взять кредит 1,5 млн рублей. Погашение кредита происходит раз в год равными суммами ( кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?
Решение:
Кредит (S) 1500000 руб.
Ставка (r) 10% годовых. Введём коэффициент b=1+0,01r
Ежегодная выплата (х) ≤350000 руб.
| Год | Долг с % | Платёж | Долг после выплаты |
| 1 | 1500000•1,1=1650000 | 350000 | 1300000 |
| 2 | 1300000•1,1=1430000 | 350000 | 1080000 |
| 3 | 1080000•1,1=1188000 | 350000 | 838000 |
| 4 | 838000•1,1=921800 | 350000 | 571800 |
| 5 | 571800•1,1=628980 | 350000 | 278980 |
| 6 | 278980•1,1=306878 | 306878 | 0 |
Ответ: 6 лет.
Задача №2
1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3% на оставшуюся сумму долга (то есть увеличивает долг на 3%), затем Андрей Владимирович переводит в банк платеж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
[МИФ] Математика ЕГЭ. Финансовая математика. Кредит на развитие бизнеса. № 513106
Задача №3.
1 января 2015 года Павел Витальевич взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платеж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?
2 тип: Нахождение суммы кредита.
S -? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12%), затем Сергей переводит в банк 3512320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами ( то есть за три года)?
Решение:
Ставка (r) — 12% , b=1,12
Ежегодная выплата (х) — 3512320 рублей
Количество лет (n) 3 года
Сумма кредита (S) -?
| Год | Долг с % | Платёж | Долг после выплаты |
| 1 | Sb | х | Sb-x |
| 2 | b(Sb-x)= Sb 2 -xb | х | Sb 2 -xb-x |
| 3 | b(Sb 2 -xb-x )= Sb 3_ хb 2 -xb | х | 0 |
Sb 3_ хb 2 -xb –x = 0
Ответ: 8436000рублей.
Задача №2.
31 декабря 2014 года Игорь взял в банке некоторую сумму в кредит под 13% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 13%), затем Игорь переводит в банк 5107600 рублей. Какую сумму взял Игорь в банке, если он выплатил долг двумя равными платежами ( то есть за два года)?
Задача№3.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами ( то есть за четыре года)?
тип: Нахождение ежегодного ( ежемесячного) транша.
х-? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Алексей взял в банке 9282000рублей в кредит по 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( то есть за четыре года)?
Решение:
Сумма кредита (S)- 9282000рубля
Количество лет (n) 4 года
Ежегодная выплата ( транш) Х -?
| Год | Долг с % | Выплата | Долг после выплаты |
| 1 | Sb | x | Sb-x |
| 2 | (Sb-x)b=Sb 2 -xb | x | Sb 2 -xb-x |
| 3 | (Sb 2 -xb-x)b=Sb 3 -x b 2 -xb | x | Sb 3 -x b 2 -xb-x |
| 4 | (Sb 3 -x b 2 -xb-x)b= Sb 4 -xb 3 -xb 2 -xb | x | 0 |
Sb 4 -xb 3 -xb 2 -xb – x = 0
Sb 4 -(b+b 2 +b 3 )x=x
Sb 4 -(1+b+b 2 +b 3 )x=0 X=
Ответ: 2928200 рублей.
Задача №2.
31 декабря 2014 года Иван взял в банке 4230000 рублей в кредит по 11,5% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11,5%), затем Иван переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Иван выплатил долг двумя равными платежами ( то есть за два года)?
Задача №3.
31 декабря 2014 года Павел взял в банке 6327000 рублей в кредит по 12% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12%), затем Павел переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Павел выплатил долг тремя равными платежами ( то есть за три года)?
4 тип : Нахождение разницы. (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 6951000 рублей
Ставка (r) -10%, b=1,1
3 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 1 | Sb | х | Sb-x |
| 2 | b(Sb-x)= Sb 2 -xb | х | Sb 2 -xb-x |
| 3 | b(Sb 2 -xb-x )=Sb 3_ хb 2 -xb | х | 0 |
Sb 3 — хb 2 -xb – x = 0
2 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | 0 |
За три года: 2795100 3=8385300
За два года:4005100 2=8010200
Ответ: на 375100 рублей.
Задача №2.
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Степан переводит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Задача №3.
31 декабря 2014 года Алексей взял в банке 3689000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк платеж. Весь долг Алексей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Задачи, связанные с известным остатком. (Фиксированные платежи)
Задача №1.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (5%)
b=1+0,01r – коэффициент (1,05)
| Месяц | Долг с % | Выплата | Долг после выплаты |
| 15.02 | Sb | Sb-0,9S | 0,9S |
| 15.03 | 0,9Sb | 0,9Sb -0,8S | 0,8S |
| 15.04 | 0,8Sb | 0,8Sb -0,7S | 0,7S |
| 15.05 | 0,7Sb | 0,7Sb -0,6S | 0,6S |
| 15.06 | 0,6Sb | 0,6Sb -0,5S | 0,5S |
| 15.07 | 0,5Sb | 0,5Sb | Полная выплата — остаток 0 |
Общая сумма выплат:
Ответ : 22,5 процента .
Задача №2.
15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,2 млн рублей.
Задача №3.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) | S | 0,7S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Дата добавления: 2021-04-15 ; просмотров: 109 ; Мы поможем в написании вашей работы!
Источник: studopedia.net
Предприятие получило в коммерческом банке кредит на сумму 126 млн рублей сроком на 3 года
Встречаются задачи, в которых долг по кредиту уменьшается неравномерно, а убывает согласно данным, представленным в таблице.
Задачи для разбора взяты с сайта РЕШУ ЕГЭ .
Задача 1. Рассчитываем разницу между общей суммой выплат и суммой самого кредита
15 января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
При решении данной задачи воспользуемся советами, данными в прошлой статье «Проценты по кредиту с равными платежами».
Учитываем, что общая сумма выплат будет превышать сумму кредита за счёт начисленных и уплаченных процентов.
I способ — решим задачу в общем виде, приняв за сумму кредита S руб. р = 5% = 0,05,
Представим решение в виде таблицы.
| Долг с начисленными процентами, руб. | Выплата, руб. | Остаток долга, руб. | Остаток долга, % | |
| Февраль | Sr | Sr — 0,9S | 0,9S | 90% |
| Март | 0,9Sr | 0,9Sr — 0,8S | 0,8S | 80% |
| Апрель | 0,8Sr | 0,8Sr — 0,7S | 0,7S | 70% |
| Май | 0,7Sr | 0,7Sr — 0,6S | 0,6S | 60% |
| Июнь | 0,6Sr | 0,6S r — 0,5S | 0,5S | 50% |
| Июль | 0,5Sr | 0,5Sr | 0 | 0% |
Общая сумма выплат составит:

Общая сумма выплат от суммы кредита:

Следовательно, переплата равна 22,5%.
II способ — используем частный случай.
Пусть сумма кредита равна 100 руб.
| Долг с начисленными процентами, руб. | Выплата, руб. | Остаток долга, руб. | Остаток долга, % | |
| Февраль | 100 * 1,05 = 105 | 105 — 90 = 15 | 90 | 90% |
| Март | 90 * 1,05 = 94,5 | 94,5 — 80 = 14,5 | 80 | 80% |
| Апрель | 80 * 1,05 = 84 | 84 — 70 = 14 | 70 | 70% |
| Май | 70 * 1,05 = 73,5 | 73,5 — 60 = 13,5 | 60 | 60% |
| Июнь | 60 * 1,05 = 66,3 | 66,3 — 50 = 13 | 50 | 50% |
| Июль | 50 * 1,05 = 52,5 | 52,5 | 0 | 0% |
Общая сумма выплат:

Следовательно, переплата равна 22,5%.
Задача 2. Рассчитываем наибольшее значение процентов, при котором общая сумма выплат будет меньше заданного числа
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:
- 1—го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн руб.
Выплата, млн руб.
Остаток долга, млн руб.
Обратите внимание! Ежемесячная выплата рассчитывается как разность между долгом на начало месяца и остатком долга. Следовательно, третий столбец заполняется в последнюю очередь.
Общая суммы выплат:


Обратите внимание! Вычисление следует производить до тысячных.
По условию задачи, r — целое число, следовательно, r = 7%.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Инвестор получил кредит в банке в сумме 150,0 млн. руб. сроком на 3 года под 20% годовых (сложные проценты). Определить сумму погашения долга в конце срока.
S = 150(1+0,2) 3 — 259,2 млн. руб.
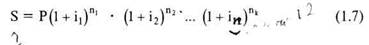
Зачастую банки, предоставляя долгосрочные кредиты, используют изменяющиеся во времени, но заранее фиксированные для каждого периода ставки сложных процентов. В этом случае наращенная сумма может быть определена по формуле:
ip i2 . Vu) — последовательные значения ставок процентов;
Пр п2 . nk — периоды, в течение которых используются соответствующие ставки.
Строительная фирма получила кредит в банке на сумму 100,0 млн. руб. сроком на 5 лет;
процентная ставка по кредиту определена в 10,5% для 1-го года, для 2-го предусмотрена надбавка к процентной ставке в размере 1,5%, для 3-го года и последующих лет — в размере 0,75%.
Определить сумму долга, подлежащую погашению в конце сро
ка займа:
S = 100 • 1,105 • 1,12 • 1,1275 3 = 177,39 млн. руб.
Использование в финансовых вычислениях простых и сложных процентов дает неодинаковые результаты, различия между ними обусловлены сроками сделок.
Так, при равной величине простых и сложных процентных ста-
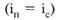
вок при сроке ссуды менее одного года (п 1) наращение по сложным процентам опережает наращение по простым процентам (1 + ni^)
Источник: nebankir.ru
