Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на (10%) по сравнению с началом года. По договоренности с банком в конце первого и третьего годов заемщик выплачивает только проценты по кредиту, начисленные за соответствующий текущий год. В конце второго и четвертого годов заемщик выплачивает одинаковые суммы, погашая к концу четвертого года весь долг полностью. Найдите наименьший размер кредита в млн. рублей, при котором общая сумма выплат заемщика превысит (100) млн. рублей.
(Задача от подписчиков)
Пусть (A) – сумма кредита в млн. рублей, а (x) – сумма выплаты во второй и четвертый годы в млн. рублей. Составим таблицу: [begin <|l|c|c|c|c|>hline texttext text\ text%\ hline 1A+0,1A0,1A\ hline 21,1Ax\ hline 3(1,1A-x)+0,1(1,1A-x)0,1(1,1A-x)\ hline 41,1(1,1A-x)x\ hline end]
Т.к. в конце четвертого года заемщик выплатил весь кредит, то сумма долга после выплаты будет равна нулю, то есть [1,1(1,1A-x)-x=0quadLeftrightarrowquad x=dfracA quad (*)] Т.к. общая сумма выплат заемщика должна превысить (100) млн. рублей, то получаем следующее неравенство: [0,1A+x+0,1(1,1A-x)+x>100quadLeftrightarrowquad 21A+190x>10,000.] Подставим в это неравенство выражение ((*)) и получим: [A>dfracquadRightarrowquad A>76. ] Т.к. (A) – целое число млн. рублей, то наименьшее (A=77) млн. рублей.
[МИФ] Математика ЕГЭ. Финансовая математика. Кредит на развитие бизнеса. № 513106
Задание 9 #3149
Уровень задания: Равен ЕГЭ
В начале марта в банке был взят кредит на 6 месяцев на следующих условиях:
— 13 числа каждого месяца, начиная с марта, на текущий долг начисляется некоторое количество процентов;
— с 14 по 29 числа каждого месяца заемщик обязан внести платеж в счет погашения кредита так, чтобы сумма долга на 13 число каждого месяца удовлетворяла следующей таблице: (begin <|l|c|c|c|c|c|c|c|>hline text 13.04 13.06 13.08 1,1A 0,77A 0,44A 0\ hline end) где (A) – сумма, взятая в кредит.
Определите наибольший месячный платеж по такому кредиту, если известно, что переплата по кредиту составила (111,000) рублей.
Если в кредит было взято (A) рублей, а в первый месяц пользования кредитом после начисления процентов долг стал равен (1,1A) рублей, то [1,1=dfrac,] где (y) – процентная ставка в банке. Следовательно, решая уравнение, находим, что (y=10%) .
Составим новую таблицу, в которой будем следить за тем, как меняется сумма долга ДО начисления процентов (например, чему равна сумма долга 12 числа каждого месяца). [begin <|l|c|c|c|c|c|c|c|>hline text 12.04 12.06 12.08 \[0.5ex] text dfrac=0,85A dfrac=0,6A dfrac=0,15A \[0.5ex] hline end] Следовательно, платежи в каждый месяц равны: [begin x_2=0,1cdot 0,85A+0,15A=0,235A\ x_4=0,1cdot 0,6A+0,2A=0,26A\ x_6=0,1cdot 0,15A+0,15A=0,165A end] Тогда наибольший платеж — это (x_5) .
Для того, чтобы найти (x_5) , нужно найти (A) . Для этого используем условие про переплату. Переплата равна: [111,000=0,1A+0,1cdot 0,85A+0,1cdot 0,7A+ 0,1cdot 0,6A+0,1cdot 0,4A+0,1cdot 0,15A = 0,37A quadRightarrowquad A=dfrac=300,000] Таким образом, [x_5=0,29A=87,000]
Задание 10 #2073
Уровень задания: Сложнее ЕГЭ
Марина взяла кредит в банке на 4 года на следующих условиях:
– раз в год банк начисляет на текущий долг (12,5%) , после чего Марина обязана внести платеж в счет погашения кредита;
– платеж в первый год в два раза меньше платежа во второй год и в три раза меньше платежа в третий год; платеж в четвертый год в 2 раза больше платежа во второй год.
Сколько процентов от суммы кредита Марина заплатит банку? В случае необходимости результат округлите до целого числа.
Пусть Марина взяла в долг у банка (A) рублей. Пусть в первый год платеж Марины равен (x) рублям. Тогда, исходя из условия задачи, (2x) – платеж во второй год, (3x) – в третий, (4x) – в четвертый. Составим таблицу:
[begin <|l|c|c|>hline text text \ hline 1 1,125cdot A-x \ hline 2 1,125(1,125cdot A-x)-2x \ hline 3 1,125(1,125(1,125cdot A-x)-2x)-3x\ hline 4 1,125(1,125(1,125(1,125cdot A-x)-\ -2x)-3x)-4x\ hline end]
Тогда имеем следующее уравнение (т.к. к концу четвертого года долг банку равен нулю):
(1,125(1,125(1,125(1,125cdot A-x)-2x)-3x)-4x=0 quad Leftrightarrow )
(Leftrightarrow quad 1,125^4cdot A-x(1,125^3+2cdot 1,125^2+3cdot 1,125+4)=0)
Заметим, что всего Марина за время пользования кредитом заплатила банку (x+2x+3x+4x=10x) рублей. Значит, необходимо найти величину:
Выразим из полученного уравнения (x) :
Значит, необходимо найти:
Заметим, что (1,125=frac98) . Следовательно:
Выполнив деление в столбик (6561div 46408) , получим (0,1413. ) , тогда все выражение равно (141,3. )
Округляя до целого числа, получим (141%) .
Задание 11 #3150
Уровень задания: Сложнее ЕГЭ
10 января в банке был взят кредит на 6 лет на следующих условиях:
— 16 числа каждого месяца, начиная с января, на текущий долг начисляется (r) процентов;
— с 17 по 28 числа каждого месяца заемщик обязан внести платеж в счет погашения кредита так, чтобы сумма долга на 10 число каждого месяца удовлетворяла следующей таблице: (begin <|l|c|c|c|c|c|c|c|>hline text 10.02 10.04 10.06 A 0,65A 0,25A 0\ hline end) Известно, что (rleqslant 10) , наибольший платеж по кредиту равен (517,125) рублей, наименьший – (187,250) рублей. Определите, сколько рублей составила переплата по кредиту.
Пусть (p=0,01r) , тогда (pleqslant 0,1) . Составим таблицу: [begin <|l|c|c|c|>hline text text A pA+0,2A=x_1 \ hline 02 0,8A+pcdot 0,8A 0,65A pcdot 0,65A+0,25A=x_3\ hline 04 0,4A+pcdot 0,4A 0,25A pcdot 0,25A+0,15A=x_5\ hline 06 0,1A+pcdot 0,1A x_4>x_5>x_6) (действительно, например, (x_2>x_4) , так как (0,8p>0,4p) , потому как (p) положительное, а второе слагаемое у них одинаковое).
Также (x_1>x_2) . Следовательно, претенденты на наибольший платеж – это (x_1) и (x_3) . Так как (0
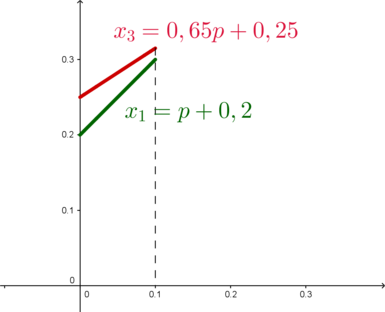
Следовательно, видим, что (x_3>x_1) при любом (pin (0;0,1]) . Таким образом, наибольший платеж – это (x_3) .
Определим наименьший платеж. Из предыдущих рассуждений заключаем, что (x_3>x_1>x_2>x_4>x_5>x_6) . Таким образом, наименьший платеж – это (x_6) .
Следовательно: [begin (0,65p+0,25)A=517,125\ (0,1p+0,1)A=187,250 end quadLeftrightarrowquad begin A=1,750,000\ p=0,07 end]
Тогда переплата по кредиту равна [begin =0,07cdot 1,750,000cdot (1+0,8+0,65+0,4+0,25+0,1)=392,000 end]
Задание 12 #2369
Уровень задания: Сложнее ЕГЭ
4 января Валентина оплатила покупку со своей кредитной карты на (800,000) рублей. Условия пользования кредитной картой таковы:
— 10 и 30 числа каждого месяца на текущий долг начисляется (4%) ;
— между 10 и 30 числами каждого месяца Валентина имеет возможность внести на карту любую сумму, причем эта сумма идет сначала на погашение начисленных процентов, а оставшаяся часть — на погашение части основного долга. Таким образом, основной долг уменьшается;
— если внесенная таким образом сумма не превышает сумму начисленных процентов, то основной долг не меняется, и происходит лишь погашение части суммы начисленных процентов;
— 1 числа каждого месяца, начиная с февраля, Валентина должна вносить обязательный платеж по карте так, чтобы сумма долга (в процентах от кредита) уменьшалась согласно таблице:
Сколько процентов от стоимости покупки составит переплата Валентины за совершенную покупку, если помимо обязательных платежей 20 числа каждого месяца Валентина будет вносить на карту (10,000) рублей?
Введем обозначения: (A=800,000) рублей – сумма, оплаченная по кредитной карте, (t=1,04) , (x=10,000) рублей.
[small <|c|c|c|c|c|>hline text texttext\ hline A tA-x a_1\ hline 0,9A tcdot 0,9A-x a_2\ hline 0,7A tcdot 0,7A-x a_3\ hline 0,5A tcdot 0,5A-x a_4\ hline 0,2A tcdot 0,2A-x a_5\ hline end>]
Вычислим (a_i) обязательные платежи. Т.к. до первого обязательного платежа долг был равен (t(tA-x)) , а после платежа должен стать равным (0,9A) , то платеж (a_1=t(tA-x)-0,9A=t^2A-tx-A+0,1A=(t^2-1)A-tx+0,1A) (расписали (0,9A=A-0,1A) ).
Аналогично второй платеж (a_2=t^2cdot 0,9A-tx-0,7A=t^2cdot 0,9A-tx-0,9A+0,2A=(t^2-1)cdot 0,9A-tx+0,2A) ;
третий платеж (a_3=(t^2-1)cdot 0,7A-tx+0,2A) ;
четвертый платеж (a_4=(t^2-1)cdot 0,5A-tx+0,3A) ;
пятый платеж (a_5=(t^2-1)cdot 0,2A-tx+0,2A) .
Общая сумма выплат по данной карте равна сумме платежей в (x) рублей (их было 5) плюс сумма обязательных платежей:
(5cdot x+a_1+a_2+a_3+a_4+a_5=5x+(t^2-1)cdot Acdot(1+0,9+0,7+0,5+0,2)-5tx+)
Тогда переплата по кредитной карте равна общей сумме выплат за вычетом суммы, взятой в кредит, то есть за вычетом (A) , то есть переплата равна (5x+(t^2-1)cdot 3,3A-5tx) .
Значит, относительно суммы кредита переплата составила:
Задание 13 #2839
Уровень задания: Сложнее ЕГЭ
Планируется выдавать кредит сроком на 3 года на следующих условиях:
— в первый и третий годы клиент обязан вносить в счет погашения кредита одну и ту же сумму;
— во второй год клиент обязан вносить в счет погашения кредита только проценты, начисленные за соответствующий текущий год.
Под какое наименьшее целое кратное десяти число процентов годовых необходимо выдавать такой кредит, чтобы общая сумма выплат по кредиту составляла не менее (150%) от суммы кредита?
Пусть кредит выдается на сумму (A) рублей, а платеж, который вносит клиент в первый и третий годы, равен (x) рублей. Пусть также (y%) – годовой процент по кредиту; тогда введем переменную (1+0,01y=p) . Составим таблицу:
Заметим, что в таблице мы для наглядности записывали (0,01y) , а не (p-1) .
Т.к. кредит в конце третьего года должен быть выплачен полностью, то получаем следующее уравнение:
[p(pA-x)-x=0 quad Rightarrow quad p^2A-x(p+1)=0]
По условию задачи общая сумма выплат должна составлять не менее (150%) от суммы кредита (A) . Значит, имеем следующее неравенство (будем писать вместо (0,01y) выражение (p-1) ):
[x+(p-1)(pA-x)+xgeqslant 1,5A quad Rightarrow quad A(p^2-p)+x(3-p)geqslant 1,5A]
Выразим из вышеполученного уравнения (x=dfrac) и подставим в неравенство:
[A(p^2-p)+(3-p)cdot dfracgeqslant 1,5A quad Rightarrow quad dfracgeqslant 0]
Т.к. (p+1>0) , то решение данного неравенства совпадает с решением неравенства (6p^2-5p-3geqslant 0) .
Т.к. (y) кратно десяти, то возможные варианты для (p) – это (1,1; 1,2; 1,3) и т.д. Подставим по очереди каждое число и найдем наименьшее подходящее.
Таким образом, это (p=1,3) : (6cdot 1,3^2-5cdot 1,3-3=0,64>0) .
Задание 14 #2368
Уровень задания: Сложнее ЕГЭ
1 марта Евгений оплатил покупку со своей кредитной карты на (1,000,000) рублей. Условия пользования кредитной картой таковы:
— долг по карте необходимо погасить в течение 5 месяцев;
— 9 и 27 числа каждого месяца на текущий долг начисляется (0,1%) ;
— между 9 и 27 числами каждого месяца Евгений имеет возможность внести на карту любую сумму, причем эта сумма идет сначала на погашение начисленных процентов, а оставшаяся часть — на погашение части основного долга. Таким образом, основной долг уменьшается;
— если внесенная таким образом сумма не превышает сумму начисленных процентов, то основной долг не меняется, и происходит лишь погашение части суммы начисленных процентов;
— с 28 числа и до конца месяца Евгений должен внести обязательный платеж по карте так, чтобы сумма долга каждый месяц уменьшалась на одну и ту же величину.
Сколько рублей составит переплата Евгения за совершенную покупку, если помимо обязательных платежей 15 числа каждого месяца Евгений будет вносить на карту (1000) рублей?
Т.к. сумма долга каждый месяц должна уменьшаться на одну и ту же величину, а долг необходимо погасить за 5 месяцев, то это значит, что долг разбили на 5 равных частей и каждый месяц он уменьшается на одну такую часть. То есть если долг был равен (A) рублей, то в конце первого месяца он будет равен (A-frac15A=A-0,2A=0,8A) , в конце второго: (0,8A-0,2A=0,6A) , в конце третьего: (0,6A-0,2A=0,4A) и т.д.
Составим таблицу. Для удобства введем обозначения: (A=1000) тыс. рублей, (1,001=t) :
[small <|c|c|c|c|c|>hline text texttext\ hline A tA-1 a_1\ hline 0,8A tcdot 0,8A-1 a_2\ hline 0,6A tcdot 0,6A-1 a_3\ hline 0,4A tcdot 0,4A-1 a_4\ hline 0,2A tcdot 0,2A-1 a_5\ hline end>]
Вычислим (a_i) платежи. Т.к. до первого обязательного платежа долг был равен (t(tA-1)) , а после платежа должен стать равным (0,8A) , то платеж (a_1=t(tA-1)-0,8A=t^2A-t-A+0,2A=(t^2-1)A-t+0,2A) (расписали (0,8A=A-0,2A) ).
Аналогично второй платеж (a_2=t^2cdot 0,8A-t-0,6A=t^2cdot 0,8A-t-0,8A+0,2A=(t^2-1)cdot 0,8A-t+0,2A) ;
третий платеж (a_3=(t^2-1)cdot 0,6A-t+0,2A) ;
четвертый платеж (a_4=(t^2-1)cdot 0,4A-t+0,2A) ;
пятый платеж (a_5=(t^2-1)cdot 0,2A-t+0,2A) .
Общая сумма выплат по данной карте равна сумме платежей в (1) тыс.рублей (их было 5) плюс сумма обязательных платежей:
(5cdot 1+a_1+a_2+a_3+a_4+a_5=5+(t^2-1)cdot Acdot(1+0,8+0,6+0,4+0,2)-5t+5cdot 0,2 A=)
Тогда переплата по кредитной карте равна общей сумме выплат за вычетом суммы, взятой в кредит, то есть за вычетом (A) :
[left(5+(t^2-1)cdot 3A-5t+Aright)-A=3Acdot (t^2-1)-5(t-1) quad Rightarrow]
Делая подстановку (A=1000) , (t=1,001) , получим:
[Rightarrow quad 3cdot 1000cdot 2,001cdot 0,001-5cdot 0,001= 5,998text< тыс.рублей>=5998 text< рублей>]
Источник: shkolkovo.net
Задача о кредите в банке. Демо ЕГЭ по математике, задание 17.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы: — 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей. Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

Валерий Волков 5 24.12.2016
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
Новости образования
 | Министерство просвещения возвратит в российские школы серебряные медали |
 | Генпрокурор РФ назвал недостоверной половину заключений о готовности школ к учебному году |
 | Перевод баллов ОГЭ-2023 в оценку |
 | Большинство учителей поддерживает запрет фото и видеосъемки во время уроков |
 | Поздравляем всех женщин с праздником 8 марта! |
Выбор видеоурока
ЕГЭ по математике
ГИА по математике
Математика. 5 класс.
Математика. 6 класс.
Математика. 7 класс.
Математика. 8 класс.
Математика. 9 класс.
Математика. 10 — 11 класс.
Создаёте видеоуроки?
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.


Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены
Источник: www.uchportal.ru
Рубрика: Экономические (финансовые) задачи
В августе 2029 года Константин Егорович планирует взять кредит на 5 лет в размере 990 тысяч рублей. Условия его возврата таковы:
— каждый март долг возрастает на r % по сравнению с концом предыдущего года;
— с апреля по июль каждого года необходимо выплатить одним платежом часть долга;
— в июле 2030, 2031 и 2032 годов долг остается равным 990 тысяч рублей;
— выплаты в 2033 и 2034 годах равны;
— к августу 2034 года долг будет выплачен полностью.
Найдите r, если известно, что общий размер выплат равен 1 млн 890 тысяч рублей.
(ЕГЭ. Математика. Подготовка к ЕГЭ — 2022. Профильный уровень. 40 тренировочных вариантов по демоверсии 2022 года / под ред.
Ф.Ф. Лысенко, С.Ю. Кулабухова, 2021)
Решение задач экономического содержания (Cистема подготовки к ЕГЭ)
В июне 2028 года Антон Вячеславович планирует взять кредит на 5 лет в размере 920 тысяч рублей. Условия его возврата таковы:
— каждый февраль долг возрастает на r % по сравнению с концом предыдущего года;
— с марта по апрель каждого года необходимо выплатить одним платежом часть долга;
— в июне 2029, 2030 и 2031 годов долг остается равным 920 тысяч рублей;
— выплаты в 2032 и 2033 годах равны;
— к июню 2033 года долг будет выплачен полностью.
Найдите r, если известно, что общий размер выплат равен 2 млн 180 тысяч рублей.
(ЕГЭ. Математика. Подготовка к ЕГЭ — 2022. Профильный уровень. 40 тренировочных вариантов по демоверсии 2022 года / под ред. Ф.Ф.
Лысенко, С.Ю. Кулабухова, 2021)
Решение задач экономического содержания (Система подготовки к ЕГЭ)
В июле 2019 года планируется взять кредит в банке на три года в размере S млн рублей, где S – целое число. Условия его возврата таковы: каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле каждого года долг должен составлять часть кредита в соответствии со представленной таблицей. Найдите наименьшее S, при котором каждая из выплат будет больше 3 млн. руб.
(ЕГЭ-2019. Досрочный период. 29 марта 2019)
Николай Сергеевич взял кредит 1 февраля 2015 года на сумму S млн рублей. Условия его возврата таковы:
— 1 марта года сумма долга увеличивается на 10% по сравнению с февралем этого года;
— с 1 мая по 1 августа необходимо выплатить часть долга;
— 28 февраля каждого года долг должен составлять часть кредита в соответствии с таблицей, указанной в задаче.
(Начиная с 2019 года долг равномерно уменьшается на 200 000 рублей в год.)
В каком году Николай Сергеевич планирует совершить последний платеж, если общая сумма выплат равна 17 680 000 рублей?
(Математика. Подготовка к ЕГЭ / под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова)
Друзья! Очень много вопросов поступает о том, что при решении задачи в ответе получается 2044, а в таблице ответов, которая указана в сборнике тестов записано 2045. Я получила официальный комментарий от Сергея Юрьевича Кулабухова (автора задачи). Сергей Юрьевич благодарит всех за внимательное прочтение книги и сожалеет, что при печати книги была допущена опечатка. Правильный ответ: 2044
15 декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысяч рублей? (ЕГЭ-2018, основной период – 1 июня 2018)
Решение задач экономического содержания (банковские вклады и кредиты) (Система подготовки к ЕГЭ)
Валерий открыл вклад в банке, по которому банк выплачивает 8% годовых. По договору вклада он может производить расходные операции (снимать со счёта деньги) не чаще одного раза в год (после начисления банком процентов). В конце второго года Валерий снял со счёта 229000 рублей, а в конце третьего года он снял со счёта 350000 рублей, после чего сумма на счёте составила 190000 рублей. Какую сумму вносил Валерий при открытии счёта? (Математика. Подготовка к ЕГЭ / Д. А. Мальцев и др.)
Решение задач экономического содержания (Система подготовки к ЕГЭ)
В регионе А среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%. В регионе В среднемесячный доход на душу населения в 2014 году составлял 60 000 рублей. В течение трёх лет суммарный доход жителей региона В увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах А и В стал одинаковым. Найдите m. (ЕГЭ-2018, досрочный период – 11 апреля 2018 — 11.04.2018)
В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен четырьмя равными платежами (то есть за 4 года) и общая сумма выплат составила 311040 рублей. (ЕГЭ-2018, досрочный период – 30 марта 2018)
Пенсионный фонд владеет ценными бумагами, которые стоят ( t^2 ) тыс. рублей в конце года t ( t = 1; 2; …). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счет в банке, при этом в конце каждого следующего года сумма на счете будет увеличиваться в (1 + r) раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счете была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
ВНИМАНИЕ. ДОПОЛНЕНИЕ К ВИДЕОРАЗБОРУ.
Сравниваем именно 20 и 22 год, т.к. при ежегодном увеличении вклада в n раз, число n стремиться к единице. Данное утверждение следует из того, что ( n=((t+1)^2):t^2 ) стремится к 1. Другими словами, ежегодно сумма вклада возрастает на некоторую сумму денег (руб), разность между суммами последующего года и предыдущего с каждым годом увеличивается, НО если смотреть во сколько раз она увеличивается (а это как раз есть наше число n), то делаем вывод, что с каждым годом это число n уменьшается. Поэтому, есть такой год, когда n меньше 1+r . В условии говорится, что такая ситуация наступает строго в конце 21 года. Поэтому сравниваем со значениями 20 и 22 годов.
Задача 1 (из учебника Н.Я. Виленкина Математика 6 класс): Банк купил несколько акций завода и через год продал их за 576,8 млн рублей, получив 3% прибыли. Какую сумму банк затратил на приобретение акций?
Задача 2: В банк внесен вклад 550 млн рублей под 11% годовых. Какая сумма денег будет на счете через год? Через три года?
Задача 3: (с сайта www.egemaximum.ru): 31 декабря текущего года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), а затем Алексей переводит в банк x рублей. Какой должна быть сумма х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за 4 года)?
Рубрики
- Готовимся к ЕГЭ вместе
- Новости
- Видеоуроки
- Математика 5-6
- Простейшие уравнения
- Текстовые задачи
- Экономические (финансовые) задачи
- Задачи с параметром
- Показательные и логарифмические неравенства
- Тригонометрические уравнения
- Начала анализа
- 10 класс
- Стереометрия
- Планиметрия
Источник: www.margolis-ov.ru
