х-? (Аннуитетные платежи)
31 декабря 2014 года Алексей взял в банке 9282000рублей в кредит по 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( то есть за четыре года)?
Решение:
Сумма кредита (S)- 9282000рубля
Количество лет (n) 4 года
Ежегодная выплата ( транш) Х -?
| Год | Долг с % | Выплата | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | x | Sb-x |
| 2 год | (Sb-x)b=Sb 2 -xb | x | Sb 2 -xb-x |
| 3 год | (Sb 2 -xb-x)b=Sb 3 -x b 2 -xb | x | Sb 3 -x b 2 -xb-x |
| 4 год | (Sb 3 -x b 2 -xb-x)b= Sb 4 -xb 3 -xb 2 -xb | x | Полная выплата — остаток 0 |
Sb 4 -xb 3 -xb 2 -xb =x
Sb 4 -(b+b 2 +b 3 )x=x
Sb 4 -(1+b+b 2 +b 3 )x=0
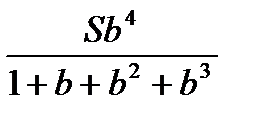
X=
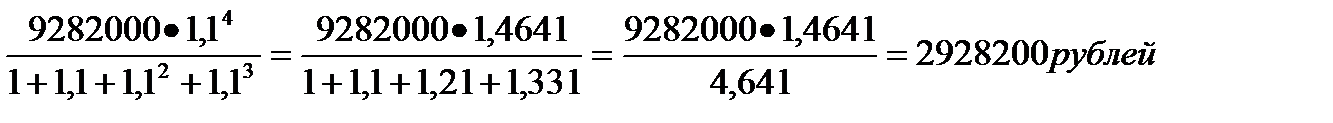
X=
Ответ: 2928200 рублей.
31 декабря 2014 года Иван взял в банке 4230000 рублей в кредит по 11,5% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11,5%), затем Иван переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Иван выплатил долг двумя равными платежами ( то есть за два года)?
Сумма кредита (S)- 4230000рубля
Ставка (а)=11,5%, b=1,115
Количество лет (n) 2 года
Ежегодная выплата ( транш) Х -?
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | — |
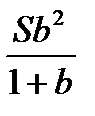
X=
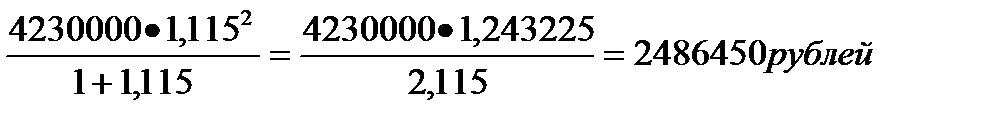
X=
Ответ: 2486450рублей.
31 декабря 2014 года Павел взял в банке 6327000 рублей в кредит по 12% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12%), затем Павел переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Павел выплатил долг тремя равными платежами ( то есть за три года)?
Решение:
Сумма кредита (S)- 6327000 рубля
Количество лет (n) 3 года
Ежегодная выплата ( транш) Х -?
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | Sb 2 -xb-x |
| 3 год | b(Sb 2 -xb-x )=Sb 3_ хb 2 -xb | х | — |
Sb 3_ хb 2 -xb =x
X= 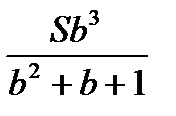 =
= 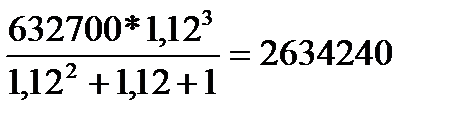
Ответ: 2634240 рублей.
5 тип : Нахождение разницы. (Аннуитетные платежи)
31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 6951000 рублей
Ставка (r) -10%, b=1,1
3 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | Sb 2 -xb-x |
| 3 год | b(Sb 2 -xb-x )=Sb 3_ хb 2 -xb | х | — |
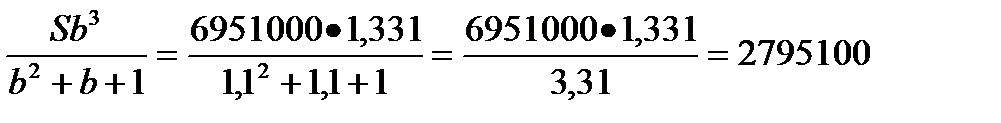
X=
2 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | — |
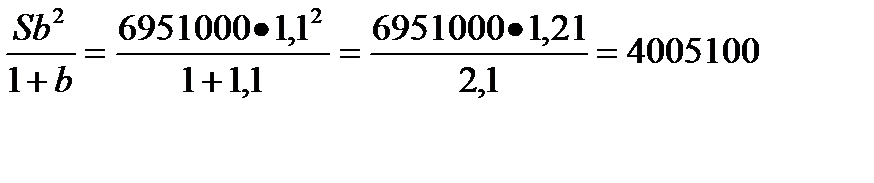
X=

За три года: 2795100 3=8385300

За два года:4005100 2=8010200
Ответ: на 375100 рублей.
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Степан переводит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 4004000 рублей
Ставка (r) -20%, b=1,2
3 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | Sb 2 -xb-x |
| 3 год | b(Sb 2 -xb-x )=Sb 3_ хb 2 -xb | х | — |
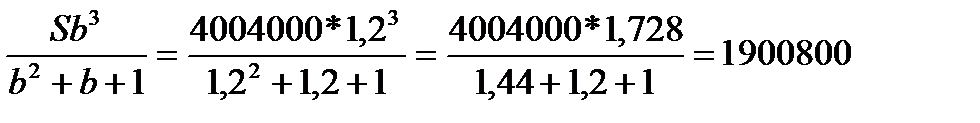
X=
2 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | — |
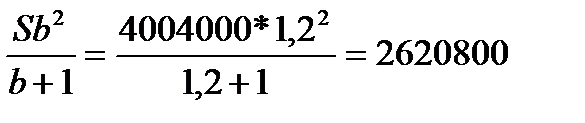
X=
За 3 года выплатил: 3*1900800=5702400
За два года: 2*2620800=5241600
Ответ: 460800 рублей.
31 декабря 2014 года Алексей взял в банке 3689000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк платеж. Весь долг Алексей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 3689000 рублей
Ставка (r) -12,5%, b=1,125
3 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb2-xb | х | Sb2-xb-x |
| 3 год | b(Sb2-xb-x )=Sb3_ хb2-xb | х | — |
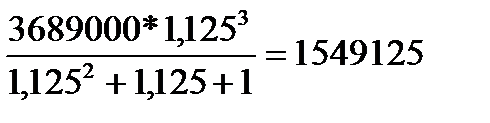
X=
2 равных платежа
| Год | Долг с % | Платёж | Долг после выплаты |
| 0 | S | ||
| 1 год | Sb | х | Sb-x |
| 2 год | b(Sb-x)= Sb 2 -xb | х | — |
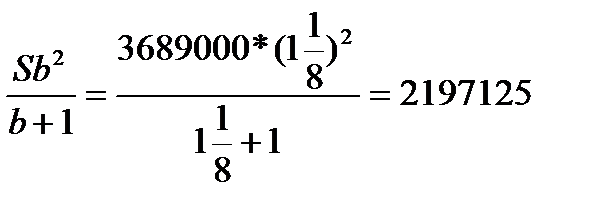
X=

За три года: 1549125 3=4647375

За два года:2197125 2=4394250
Ответ: 253125 рублей.
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (5%)
b=1+0,01r – коэффициент (1,05)
| Месяц | Долг с % | Выплата | Долг после выплаты |
| 15.01 | S | ||
| 15.02 | Sb | Sb-0,9S | 0,9S |
| 15.03 | 0,9Sb | 0,9Sb -0,8S | 0,8S |
| 15.04 | 0,8Sb | 0,8Sb -0,7S | 0,7S |
| 15.05 | 0,7Sb | 0,7Sb -0,6S | 0,6S |
| 15.06 | 0,6Sb | 0,6Sb -0,5S | 0,5S |
| 15.07 | 0,5Sb | 0,5Sb | Полная выплата — остаток 0 |
Общая сумма выплат:
Ответ : 22,5 процента .
15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,2 млн рублей.
Решение: S – сумма кредита (1000000рублей)
Найти : r% — годовые (ежемесячные) проценты
| Месяц | Долг с % | Выплата | Долг после выплаты |
| 15.01 | S | ||
| 15.02 | Sb | Sb-0,6S | 0,6S |
| 15.03 | 0,6Sb | 0,6Sb -0,4S | 0,4S |
| 15.04 | 0,4Sb | 0,4Sb -0,3S | 0,3S |
| 15.05 | 0,3Sb | 0,3Sb -0,2S | 0,2S |
| 15.06 | 0,2Sb | 0,2Sb -0,1S | 0,1S |
| 15.07 | 0,1Sb | 0,1Sb | Полная выплата — остаток 0 |
Общая сумма выплат:
Ответ: 7 процентов.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) | S | 0,7S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (15%)
b=1+0,01r – коэффициент (1,15)
| Год | Долг с % | Выплата | Долг после выплаты |
| 2016 | S | ||
| 2017 | Sb | Sb-0,7S | 0,7S |
| 2018 | 0,7Sb | 0,7Sb -0,4S | 0,4S |
| 2019 | 0,4Sb | 0,4Sb | Полная выплата — остаток 0 |
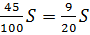
1 выплата 1,15S-0,7S= 0,45S=
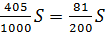
2 выплата 0,7*1,15S-0,4S= 0,405S=
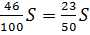
3 выплата 0,4*1,15S= 0,46S=
По условию, все выплаты должны быть целыми. Значит, число S должно делиться на 20, 200 и 50. Наименьшее общее кратное этих чисел равно 200.
Ответ: 200 тысяч.
Дата: 2019-05-29, просмотров: 2463.
Источник: findout.su
Дифференцированные платежи
Даша взяла ипотеку 6 000 000 рублей под 12% годовых на 10 лет. Выплаты подбираются так, чтобы долг уменьшался равномерно.
1) сколько всего денег Даша отдаст банку?
2) На сколько процентов больше Даша отдаст банку по сравнению с суммой, взятой в кредит
3) Сколько процентов составляет сумма выплат по сравнению с суммой, взятой в кредит?
4) Можно ли ответить на вопросы
2) и 3) не зная, сколько денег взяли в кредит?
5) Чему равен 3й платеж?
6) Чему равен наименьший платеж? Наибольший?
7) Сколько выплатит Даша за первые 6 лет?
№2 (ЕГЭ 2016)
Сергей взял в банке кредит 1,2 млн рублей на срок 24 месяца. По договору Сергей должен возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Сергеем банку в конце месяца. Суммы, выплачиваемые Сергеем, подбираются так, чтобы сумма долга уменьшалась равномерно, т.е. на одну и ту же величину каждый месяц. Какую сумму Сергей вернет банку в течение первого года кредитования?
Эмиль взял кредит в банке на срок 12 месяцев. По договору Эмиль должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Эмиль погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Эмилем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Источник: 4ege.ru
Го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения
В конце каждого месяца, начиная с января, текущий долг увеличивается на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Пусть 15 — го числа текущего месяца долг равен х рублей, а 15 го числа предыдущего месяца у рублей. Тогда в конце предыдущего месяца долг равен 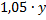 и выплата в первой половине текущего месяца равна
и выплата в первой половине текущего месяца равна  . В процентах отсуммы кредита выплаты в феврале составили
. В процентах отсуммы кредита выплаты в феврале составили 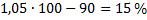 ; в марте
; в марте  в июне
в июне 
Общая сумма выплат составила 15 + 14,5 + 14 + 13,5 + 13 + 52,5 = 122,5 %.
Ответ: 22,5 %
III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
13. В июле планируется взять кредит в банке на сумму 10 млн. рублей на 5 лет. Условия его возврата таковы:
— каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Сколько млн. рублей составила общая сумма выплат после погашения кредита?
| год | кредит | долг | Выплаты |
| 1 | 10 |  |  |
| 2 | 8 |  |  |
| 3 | 6 |  |  |
| 4 | 4 |  |  |
| 5 | 2 |  | 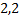 |

Найдем сумму всех выплат: .
Ответ: 13 млн. рублей.
14. В июле планируется взять кредит на некоторую сумму. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за 3 года)?
Пусть х рублей планируется взять в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 2, 16 млн. рублей после начисления 20 % на оставшуюся сумму долга.






Ответ: 4,55 млн. рублей
15. 31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12 % годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12 %), затем Сергей переводит в банк 3 512 320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами ( то есть за три года)?
Пусть х рублей взял Сергей в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 3 512 320 рублей после начисления 12% на оставшуюся сумму долга.



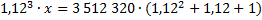


Ответ: 8 436 000.
16. Жанна взяла в банке кредит 1,8 млн. рублей на срок 24 месяца. По договору Жанна должна возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца.
Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
| Срок | Кредит | Долг | Выплаты |
| 1 | 1,8 | 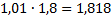 |  |
| 2 |  |  |  |
| 3 | 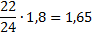 | 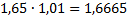 |  |
| 4 | 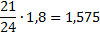 |  | |
| . | . | . |

Выплаты составляют арифметическую прогрессию, где



Ответ: 1,0665 млн. рублей.
IIспособ : Пусть  — сумма долга в конце n — го месяца,
— сумма долга в конце n — го месяца,  — первоначальная сумма долга.
— первоначальная сумма долга.


 , где
, где  По условию задачи, надо найти сумму выплат Жанны за первый год кредитования, то есть
По условию задачи, надо найти сумму выплат Жанны за первый год кредитования, то есть 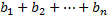 .
.

По условию задачи: сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц, тогда составляет арифметическую прогрессию, где


— формула n- го члена прогрессии.


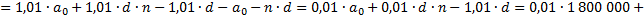



Суммы выплат составляют арифметическую прогрессию.


.
Ответ: 1 066 500.
17. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого следующего года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами ( то есть за 4 года)?
Пусть х рублей выплата по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по хруб. после начисления 20 % на оставшийся долг.

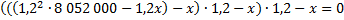
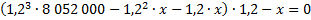




Ответ: 3 110 400
18. 31 декабря 2014 года Алексей взял в банке 9 282 000 рублей под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( за четыре года)?
Пусть Х рублей выплата Алексея по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по х руб. после начисления 10 % на оставшийся долг.





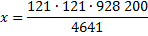

Ответ: 2 928 200.
19. Фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых. Схема погашения кредита: раз в год клиент выплачивает банку одну и ту же сумму, которая состоит из двух частей. Первая часть составляет 20 % от оставшейся суммы долга, а вторая часть направлена на погашение оставшейся суммы долга. Каждый следующий год проценты начисляются только на оставшуюся часть долга.
Какой должна быть ежегодная сумма выплат ( в рублях ), чтобы фермер полностью погасил кредит тремя равными платежами?
Пусть х рублей должна быть ежегодная сумма выплат. Составим уравнение по условию задачи:фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых и погасил кредит тремя равными платежами.






Ответ: 1 728 000.
20. В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом прошлого года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года ) по сравнению со случаем, если он будет полностью погашен двумя равными платежами ( то есть за 2 года )?
I случай. Пусть по х рублей выплачивают , чтобы погасить кредит четырьмя равными платежами. Составим первое уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили четырьмя равными платежами.
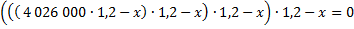





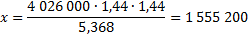
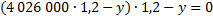
II случай. Пусть по yрублей выплачивают, что бы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили двумя равными платежами.




Вопрос задачи: на сколько рублей больше отдали бы банку, если бы выплатили долг за четыре равных платежа или найти разность
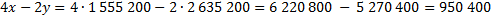
Ответ: 950 400.
21. 31 декабря 2014 года Фёдор взял в банке 6 951 000 рублей в кредит под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляют проценты на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Фёдор переводит в банк платёж. Весь долг Фёдор выплатил за три равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа?
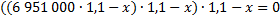
I случай. Пусть по х рублей выплачивал Фёдор, что бы погасить кредит тремя платежами. Составим первое уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил тремя равными платежами.

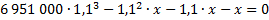



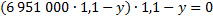
II случай. Пусть по yрублей выплачивал Фёдор, чтобы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил двумя равными платежами.

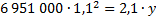


Вопрос задачи: на сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа или найти разность


Ответ: 375 100.
Дата добавления: 2018-04-05 ; просмотров: 1344 ; Мы поможем в написании вашей работы!
Источник: studopedia.net
