Цель работы – проведение оценки риска инвестиционного проекта методом анализа чувствительности.
Задачи работы:
Характеристика сущности риска инвестиционного проекта, классификация проектных рисков;
Характеристика базовых принципов и методических подходов, используемых в современной практике управления проектами, к оценке риска;
Анализ риска инвестиционного проекта методом анализа чувствительности.
ВВЕДЕНИЕ 3
1. теоретические основы оценки рисков инвестиционных проектов 5
1.1. Понятие риска инвестиционного проекта. Классификация
рисков 5
1.2. Принципы и методические подходы, используемые для оценки проектного риска 7
2. оценка риска инвестиционного проекта « студии загара» по методу анализа чувствительности 14
2.1. Концепция бизнеса 14
2.2. Анализ чувствительности проекта по показателю «Чистый приведенный доход» 16
заключение 28
список использованных источников и литературы…30
Содержимое работы — 1 файл
В качестве оказания сопутствующих услуг можно выделить в отдельное направление продажу одной или двух линий кремов для загара и одной линии кремов для ухода за кожей.
Краткий курс по количественной оценке рисков — Константин Дождиков, директор, РОСНАНО
Создаваемая студия будет предлагать клиенту альтернативный выбор из нескольких профессиональных соляриев студийного класса с различным набором дополнительных услуг.
Параметры альтернативного проекта
| Параметры проекта | Значение |
| Капиталовложения, тыс. руб. | 3000 |
| Срок реализации проекта, лет | 3 |
| Стоимость капитала, % | 15 |
| Объемы реализации продукции | 100 |
| Цена продукции, руб. | 100 |
| Себестоимость 1 т., руб. | 80 |
Существует также альтернативный проект, параметры которого приведены в табл.1.
2.2. Анализ чувствительности проектов по показателю « Чистый приведенный доход»
Проанализируем чувствительность двух проектов по показателю чистого приведенного дохода и определим лучший проект с точки зрения минимального риска.
Перед предприятием стоит задача провести анализ чувствительности проекта с целью выявления влияния основных исходных факторных показателей на его эффективность. В качестве основного показателя эффективности проекта изберем чистый приведенный доход. Анализ проводится по всему проектному циклу, продолжительность которого составляет 4 года. Для анализа чувствительности проекта отобрано 7 первичных (факторных) показателей.
В процессе анализа возможных условий реализации проекта определены минимальные и максимальные границы возможных значений первичных (факторных) показателей и рассчитаны соответствующие им значения показателя чистого приведенного дохода. Минимальные и максимальные границы возможных колебаний каждого из первичных (факторных) показателей и вызываемых этими колебаниями возможный значений чистого приведенного дохода характеризуется данными табл. 1.
Интеграция анализа рисков в финансовые модели
Исходя из приведенных данных определим диапазон возможных колебаний первичных показателей в процессе реализации проекта. Он составит:
- по первому показателю — 10% (5 + 5);
- по второму показателю — 36% (15 + 21);
- по третьему показателю — 10% (3 + 7);
Минимальные и максимальные границы возможных колебаний первичных показателей и соответствующих им возможных отклонений от чистого
денежного потока по проекту от расчетного
(В процентах к базовому)
| Показатели | Границы возможных колебаний первичных показателей, положенных в основу расчета чистого денежного дохода | Границы возможных отклонений чистого приведенного дохода в рамках колебаний, формирующих его первичные показатели | ||
| Минимальная | Максимальная | Минимальная | Максимальная | |
| 1 | 2 | 3 | 4 | 5 |
| 1. Цены на приобретаемое оборудование | -5 | +5 | -3 | +3 |
| 2. Тарифы на осуществление монтажных работ | -15 | +21 | -5 | +7 |
| 3. Стоимость привлечения инвестиционных ресурсов | -3 | +7 | -6 | +2 |
| 4. Уровень цен на продукцию | -20 | +25 | -15 | +19 |
| 5. Уровень налоговых платежей | -15 | +19 | -3 | +6 |
| 6. Структура операционных издержек | -8 | +9 | -5 | +5 |
| 7. Темп инфляции | +8 | +15 | -6 | -12 |
- по четвертому показателю — 45% (20+25);
- по пятому показателю — 34% (15 + 19);
- по шестому показателю –– 17% (8 + 9);
- по седьмому показателю –– 7% (15 – 8).
Аналогичным образом определим диапазон возможных колебаний чистого приведенного дохода в границах предполагаемых изменений первичных показателей. Он составит:
- по первому показателю — 6% (3 + 3);
- по второму показателю — 12% (5 + 7);
- по третьему показателю — 8% (6 + 2);
- по четвертому показателю — 34% (15 + 19);
- по пятому показателю — 9% (3 + 6);
- по шестому показателю –– 10% (5 + 5);
- по седьмому показателю –– 6% (–12 + 6).
На основе проведенных расчетов определим коэффициент эластичности изменения показателя чистого приведенного дохода от изменения каждого из рассматриваемых первичных показателей. Он составит:
- по первому показателю: 6/10 = 0,6;
- по второму показателю: 12/36 = 0,33;
- по третьему показателю: 8/10 = 0,8;
- по четвертому показателю: 34/45 = 0,76;
- по пятому показателю: 9/34 = 0,26;
- по шестому показателю: 10/17 = 0,59;
- по седьмому показателю: 6/7 = 0,86.
Анализ проведенных расчетов показывает, что наиболее сильное влияние на возможное изменение чистого приведенного дохода оказывает темп инфляции (коэффициент эластичности этого влияния равен 0,86), а наименьшее — пятый исходный показатель (уровень налоговых платежей). Соответственно проведенным расчетам и значению коэффициента эластичности осуществлено ранжирование первичных (факторных) показателей по степени их влияния на возможное изменение чистого приведенного дохода по проекту (табл.2).
Ранжирование первичных (факторных) показателей по результатам анализа чувствительности проекта
| Показатели | Диапазон возможных колебаний первичных показателей | Диапазон возможных колебаний чистого приведенного дохода | Коэффициент эластичности изменения чистого приведенного дохода | Ранговая значимость первичного (факторного) показателя |
| 1 | 2 | 3 | 4 | 5 |
| 1. Цены на приобретаемое оборудование | 10 | 6 | 0,60 | 4 |
| 2. Тарифы на осуществление монтажных работ оборудования | 36 | 12 | 0,33 | 6 |
| 3. Стоимость привлечения инвестиционных ресурсов | 10 | 8 | 0,80 | 2 |
| 4. Уровень цен на продукцию | 45 | 34 | 0,76 | 3 |
| 5. Уровень налоговых платежей | 34 | 9 | 0,26 | 7 |
| 6. Структура операционных издержек | 17 | 10 | 0,59 | 5 |
| 7. Темп инфляции | 7 | 6 | 0,86 | 1 |
Ранжирование первичных (факторных) показателей по результатам анализа чувствительности проекта по критерию максимизации диапазона колебаний чистого приведенного дохода
| Показатели | Диапазон возможных колебаний первичных показателей | Диапазон возможных колебаний чистого приведенного дохода | Коэффициент эластичности изменения чистого приведенного дохода | Ранговая значимость первичного (факторного) показателя |
| 1 | 2 | 3 | 4 | 5 |
| 1. Цены на приобретаемое оборудование | 10 | 6 | 0,60 | 6 |
| 2. Тарифы на осуществление монтажных работ оборудования | 36 | 12 | 0,33 | 2 |
| 3. Стоимость привлечения инвестиционных ресурсов | 10 | 8 | 0,80 | 5 |
| 4. Уровень цен на продукцию | 45 | 34 | 0,76 | 1 |
| 5. Уровень налоговых платежей | 34 | 9 | 0,26 | 4 |
| 6. Структура операционных издержек | 17 | 10 | 0,59 | 3 |
| 7. Темп инфляции | 7 | 6 | 0,86 | 7 |
Ниже проведем анализ чувствительность второго проекта.
Прежде всего, рассчитаем показатель эффективности проекта. В качестве такого показателя выберем чистый приведенный доход (ЧПД). Расчет проведем с помощью табл.4.
Доход в табл.4 рассчитан как произведение цены продукции на объем ее реализации: 100 тыс. т * 100 = 10000 тыс. руб.
Затраты рассчитаны как произведение объема реализации продукции на себестоимость 1 т: 100*80 = 8000 тыс. руб.
Денежный поток рассчитан как разница между доходом, с одной стороны, и инвестициями, затратами, с другой.
Дисконтированный денежный поток рассчитан как произведение денежного потока на дисконтный множитель, значения которого взяты из финансовых таблиц.
Для анализа чувствительности проекта отобрано 5 первичных (факторных) показателей: капиталовложения, стоимость капитала, объемы реализации продукции, цена продукции, себестоимость.
В процессе анализа возможных условий реализации проекта определены минимальные и максимальные границы возможных значений первичных (факторных) показателей и рассчитаны соответствующие им значения показателя чистого приведенного дохода. Минимальные и максимальные границы возможных колебаний каждого из первичных (факторных) показателей и вызываемых этими колебаниями возможный значений чистого приведенного дохода характеризуется данными табл.5.
Расчет чистого приведенного дохода
| Год | Инвестиции, тыс. руб. | Доход, тыс. руб. | Затраты, тыс. руб. | Денежный поток, тыс. руб. | Дисконтный множитель, коэф. | Дисконтированный денежный поток, тыс. руб. |
| 0-й | 3000 | -3000 | 1 | -3000 | ||
| 1-й | 10000 | 8000 | 2000 | 0,870 | 1740 | |
| 2-й | 10000 | 8000 | 2000 | 0,756 | 1512 | |
| 3-й | 10000 | 8000 | 2000 | 0,658 | 1316 | |
| NPV | 3000 | 30000 | 24000 | 3000 | — | 1568 |
Источник: www.turboreferat.ru
Анализ чувствительности в инвестиционном анализе
Анализ чувствительности (sensitivity analysis) проводится с целью учета и прогноза влияния изменения входных параметров (инвестиционные затраты, приток денежных средств, барьерная ставка, уровень реинвестиций) инвестиционного проекта на результирующие показатели.
Наиболее удобный вариант — это относительное изменение одного из входных параметров (пример — все притоки денежных средств минус 5%) и анализ произошедших изменений в результирующих показателях.
Для анализа чувствительности главное — это оценить степень влияния изменения каждого (или их комбинации) из входных параметров, чтобы предусмотреть наихудшее развитие ситуации в бизнес плане (инвестиционном проекте).
Таким образом, рассматривается обычно пессимистический, наиболее вероятный и оптимистический прогнозы и рассчитываются результаты инвестиционного проекта.
Результаты анализа чувствительности учитываются при сравнении взаимозаменяемых и не комплиментарных (невзаимозаменяемых с ограничением по максимальному бюджету) инвестиционных проектов. При прочих равных условиях выбирается инвестиционный проект (проекты) наименее чувствительный к ухудшению входных параметров.
В анализе чувствительности речь идет не о том, чтобы уменьшить риск инвестирования, а о том, чтобы показать последствия неправильной оценки некоторых величин. Анализ чувствительности сам по себе не изменяет факторы риска.
Формула для сравнения исходных параметров с рассчитанными по данным анализа чувствительности:
А — изменение величены в %;
Аисх — исходное (начальное) значение параметра А;
Аач — параметры рассчитанные по данным анализа чувствительности (конечное значение А).
В программе, для ввода параметров анализа чувствительности, выбираете в меню «Анализ» подменю «Анализ чувствительности».
При анализе чувствительности для выбора оптимистического и пессимистического варианта выбираются наиболее вероятные направления развития событий.
Источник: investment-analysis.ru
Научная электронная библиотека


В данном параграфе мы рассмотрим некоторые используемые на практике методы анализа предпринимательских и финансовых рисков.
Одними из простых, но при этом эффективных методов анализа рисков являются анализ чувствительности и анализ безубыточности. Анализ чувствительности заключается в оценке влияния изменений одного или нескольких исходных параметров на результирующий показатель.
Так, например, анализ чувствительности некоторого инвестиционного проекта может заключаться в оценке влияния изменения основных параметров этого проекта на показатели его эффективности. Анализ чувствительности предполагает построение определенной финансовой модели проекта, связывающей исходные параметры и результирующий показатель согласно заданному алгоритму.
Результатом анализа чувствительности является значение или интервал возможных значений результирующего показателя при изменении исходных параметров в заданных пределах. При этом используются как абсолютные, так и относительные значения. Как правило, при проведении анализа чувствительности не учитываются взаимосвязи между исходными параметрами. Однако на практике такой подход может привести к ошибочным выводам.
Рассмотрим анализ безубыточности и анализ чувствительности на следующем примере (1.12). Найдем минимальный (безубыточный) объем продаж рыбной продукции. Запишем выражение для нахождения операционной прибыли:
П = P•Q – VC•Q – FC, (1.57)
цена реализации единицы продукции;
удельные переменные затраты;
Тогда безубыточный объем реализации продукции будем равен:
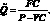
(1.58)
Пусть, даны следующие исходные условия: цена реализации единицы продукции 20 руб., удельные переменные издержки 10 руб., общий объем постоянных расходов 100 000 руб. Тогда безубыточный объем реализации:
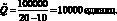
Ответим на следующий вопрос: на сколько увеличится прибыль, если объем реализации увеличится на 1000 единиц? В этом случае увеличение прибыли составит:
Для нашего примера увеличение объема реализации на 1000 единиц приведет к увеличению прибыли на 10 000 руб. На рис. 1.14 показана динамика затрат, выручки и прибыли. Прибыль изменяется линейно относительно объема реализации.
Таким образом, мы нашли минимальный объем реализации и выяснили, как будет меняться операционная прибыль при изменении объема реализации. Однако на практике такого упрощенного подхода, когда при изменении объема реализации остальные параметры остаются постоянным, как правило, бывает недостаточно. Изменение объема предложения должно сказываться на отпускных ценах. Пусть объем реализации и цена связаны следующим соотношением:
P = –0,1Q + 250. (1.60)
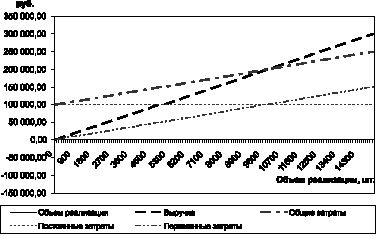
Рис. 1.14. Динамика затрат, выручки и прибыли в зависимости от изменения объема реализации
Тогда, общая величина прибыли будет равна:

(1.61)
Для нашего примера выражение для операционной прибыли примет вид:
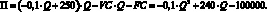
(1.62)
В отличие от соотношения (1.57), теперь выражение для прибыли представляет собой квадратное уравнение. Найдем объем реализации, при котором прибыль равна нулю (безубыточный объем реализации). Для квадратного уравнения таких решений будет два. Для нашего примера целочисленными решениями уравнения (1.62) являются значения объемов реализации 536 и 1863. В отличие от линейного уравнения прибыли, подразумевающего, что прибыль может расти бесконечно при увеличении объема реализации, для квадратного уравнения (1.62) существует объем реализации, при котором прибыль достигает максимального значения. В нашем случае:
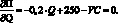
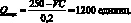
Ответим на вопрос: на сколько увеличится прибыль при увеличении объема реализации на X единиц? В отличие от линейного уравнения прибыли, где увеличение объема реализации сопровождалось пропорциональным ростом прибыли, для квадратного уравнения прирост прибыли будет разным в каждой точке, соответствующей определенному объему реализации. На рис. 1.15 представлена динамика затрат, выручки и прибыли в случае учета взаимосвязи между объемом реализации и отпускными ценами.
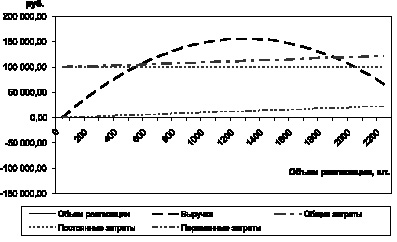
Рис. 1.15. Динамика затрат, выручки и прибыли в случае линейной взаимосвязи между объемом реализации и ценой продаж
Дальнейшим развитием анализа чувствительности являются сценарный анализ и имитационное моделирование. Сценарный анализ заключается в разработке сценариев развития ситуации, учитывающих взаимосвязи между различными факторами, и расчет показателей эффективности для каждого сценария.
Данный метод существенно дополняет возможности по анализу рисков и позволяет посмотреть на проблему комплексно. Каждый сценарий представляет собой одно из возможных состояний среды в будущем и позволяет оценить, как будет функционировать система в случае реализации того или иного сценария. Если сценарный анализ предполагает разработку нескольких сценариев возможных состояний среды и оценку эффективности функционирования системы в каждом сценарии, то имитационное моделирование позволяет смоделировать динамику всей системы, изучить ее поведение при всевозможных изменениях среды. В результате применения данного метода исследователь получает не отдельные дискретные значения анализируемых показателей, а целое распределение значений показателей. Имитационное моделирование относится к численным методам и используется тогда, когда аналитическое выражение для решения определенной задачи получить невозможно или крайне
затруднительно.
Отдельным методом анализ рисков является метод стресс-тестирования. Стресс-тестирование представляет собой инструмент оценки потенциальных потерь объекта исследования (например, финансовые результаты проекта, стоимость портфеля активов, финансовое состояние компании) в условиях, выходящих за пределы нормального его функционирования.
Стресс-тестирование оценивает потенциальное воздействие на объект исследования критических, стрессовых изменений исходных параметров (факторов риска). Стресс-тестирование позволяет моделировать воздействие или эффект исключительных, маловероятных, но при этом потенциально возможных событий. Как правило, в моделях стресс-тестирования учитываются не отдельные рисковые факторы, а их комбинации. В качестве основных методов стресс-тестирования применяются однофакторные (анализ чувствительности) и многофакторные стресс-тесты (сценарный анализ). Менее популярны методы оценки максимальных потерь и методы, основанные на теории экстремального значения.
Особое место в анализе рисков занимает теория игр. Теория игр является широко распространенной теоретической концепцией, имеющей непосредственное прикладное значение. Впервые математические аспекты теории игр были представлены в книге фон Неймана и Моргенштерна «Теория игр и экономическое поведение» в 1944г.
Применительно к экономической науке теория игр представляет собой математический метод исследования и принятия оптимальных решений в условиях неопределенности, наличия конфликта интересов и конкурирующих стратегий поведения участников с целью достижения наилучшего результата. Каждая сторона (игрок) реализует определенную стратегию, которая характеризуется набором исходов (прибыли, убытки), ее конкретный результат зависит от того, какую стратегию избрали конкуренты. Основная цель использования теории игр для решения практических задач заключается в выборе оптимальной стратегии поведения в условии конфликта (конкуренции) с другими игроками (сторонами, конкурентами) для достижения в среднем более высокого выигрыша. В условиях неопределенности для выбора наилучшей стратегии поведения в теории игр используют следующие критерии:
– критерий гарантированного результата (максиминный критерий Вальда) – данный критерий обеспечивает максимальный выигрыш из всех минимальных выигрышей, или иначе минимальный убыток из всех максимальных потерь;
– критерий оптимизма (максимакса) – данный критерий обеспечивает получение максимального выигрыша из всех максимальных выигрышей, или иначе минимальный убыток из всех минимальных убытков;
– критерий Сэвиджа – аналогичен критерию Вальда, применяется только для матрицы рисков (упущенных возможностей) и позволяет минимизировать потери;
– критерий Гурвица – в соответствии с данным критерием выбор осуществляется как комбинация самого оптимистичного и пессимистичного решения. Критерий Гурвица применяется как к матрице выигрышей, так и рисков.
Рассмотрим использование данных критериев для выбора оптимальных стратегий на следующем примере (1.13). Предположим, что некая компания планирует запустить производство новой продукции. Компания разработала три стратегии производства. Однако, спрос на новую продукцию неизвестен. На основе проведенных маркетинговых исследований был спрогнозирован уровень спроса в трех вариантах: пессимистичный, реалистичный, оптимистичный. Зададим следующую платежную матрицу:
Платежная матрица стратегий производства
Варианты прогноза спроса
Источник: monographies.ru
