Применение функции округления в большую сторону 1С Предприятие:
Процедура ОкруглитьСумму ( ) ;
Для Каждого СтрокаТЧ Из Объект . ТЧ Цикл
Если ОкруглитьВбольшуюСторну ( СтрокаТЧ . Сумма ) <> Истина Тогда
Сумма = СтрокаТЧ . Сумма ;
Сообщить ( «Стоит округлить сумму: » + СтрокаТЧ . Номенклатура + » Рекомендация: » + Окр ( Сумма+ 0.5 , 0 , 0 ) ) ;
КонецЦикла
КонецПроцедуры
// Пример функции округлить (Пример №1)
// Например число 7.1 к 8 (Целому в большую сторону)
Функция ОкруглитьВбольшуюСторну ( Сумма )
Возврат Сумма = Окр ( Сумма+ 0.5 , 0 , 0 ) ;
КонецФункции
Процедура ПриОткрытии ( Отказ )
ОкруглитьСумму ( ) ;
КонецПроцедуры
//Для округления чисел в 1С используем функцию 1С — Окр(12.55)
//1С вернет 12
//С помощью 1С ОКР можно проводить округление дробной части чисел 1С (все то, что идет после запятой), например до сотых двух знаков):
//РезультатФункции = Окр(15.2233, 2); //15.22
//С помощью 1С ОКР можно проводить округление целой части чисел 1С (то, что идет до запятой), например до тысяч (трех знаков):
Правило округления чисел
//РезультатФункции = Окр(12333, -3); //12000
Пример того как работает функция округления в большую сторону смотрите пример в *dt
Открываем второй документ “ПоступлениеТоваровИУслуг” и тут же сработает условие (проверка, нуждается ли сумма в округлении). И если да, тогда Вы получите сообщение какой товар (сумму) нужно округлить.
Для округления чисел в 1С используем функцию 1С – Окр(12.55)
С помощью 1С ОКР можно проводить округление дробной части чисел 1С (все то, что идет после запятой), например до сотых двух знаков):
РезультатФункции = Окр(15.2233, 2);
С помощью 1С ОКР можно проводить округление целой части числа 1С (то, что идет до запятой), например до тысяч (три знака):
РезультатФункции = Окр(12333, -3); //12000
Если Вы хотите больше узнать о программировании в 1С, тогда регистрируйтесь на курс: 1С 8.3 Старт >>>

Присоединяетесь к нашей группе телеграмм: Здесь вы получите ценную помощь от умного бота «Коли» (ChatGPT) + знания сотен ее участников.
Похожие записи
Источник: kuharbogdan.com
Округление чисел. Прикидки
Пусть ширина земельного участка прямоугольной формы равна 17 м, а длина − 36 м. Тогда его площадь равна 612 м 2 , или 6,12 сотки.
Однако в повседневной жизни говорят, что площадь этого участка приблизительно равна 6 соткам.
В таких случаях число 6 называют приближенным значением числа 6,12 и говорят, что число 6,12 округлили до числа 6 . Записывают 6,12 = 6 (читают: » 6,12 приближенно равно 6 «).
Земельный участок длиной 29 м и шириной 24 м имеет площадь, равную 696 м 2 , или 6,96 сотки. На практике число 6,96 округлят и скажут, что площадь участка приближенно равна 7 соткам, то есть 6,96 ≈ 7 .
Округления чисел в математике. Правила и примеры
Почему же число 7, а не 6 считают приближенным значением числа 6,96 ? Так договорились потому, что число 7 − ближайшее к 6,96 натуральное число (рис. 205 ). Следовательно, при замене числа 6,96 числом 7 совершается меньшая ошибка, чем при замене числа 6,96 числом 6 . Воспользовавшись рисунком 205, можно записать : 6,12 ≈ 6 ; 6,2 ≈ 6 ; 6,391 ≈ 6 ; 6,41 ≈ 6 ; 6,6 ≈ 7 ; 6,703 ≈ 7 ; 6,8 ≈ 7 (см. рис. 205 ).
1.3.2. Правила округления значения погрешности и записи
Погрешность результата измерений позволяет определить те цифры результата, которые являются достоверными. При расчете величины погрешности, особенно с помощью калькуляторов, значение погрешности получается с большим числом знаков. Это создает впечатление о высокой точности измерений, что не соответствует действительности, так как исходными данными для расчета чаще всего являются нормируемые значения погрешности используемого СИ, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности не следует удерживать более двух значащих цифр. В метрологии существуют следующие правила:
1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них 3 или меньше, и одной — если первая цифра есть 4 и более.
Значащими цифрами числа считаются все цифры от первой слева, не равной нулю, до последней справа цифры, при этом нули, записанные в виде множителя 10 n , не учитываются.
2. Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности. (Например, результат 85.6342, погрешность 0.01. Результат округляют до 85.63. Тот же результат при погрешности в пределах 0.012 следует округлить до 85.634).
3. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним — двумя лишними знаками.
4. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление приводит к ошибкам.
При округлении числовых значений погрешности и результата измерений необходимо руководствоваться следующими общими правилами округления.
Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. (Например, число 165245 при сохранении четырех значащих цифр округляется до 165200, а число 165.245 — до 165.2).
Если десятичная дробь оканчивается нулями, они отбрасываются только до разряда, который соответствует разряду погрешности. (Например, результат измерений 235.200, погрешность 0.05. Результат округляют до 235.20. Тот же результат при погрешности в пределах 0.015 следует округлить до 235.200).
Если первая (считая слева направо) из заменяемых нулями или отбрасываемых цифр меньше 5, остающиеся цифры не изменяются.
Если первая из этих цифр равна 5, а за ней не следует никаких цифр, или идут нули, то, если последняя цифра в округляемом числе четная или нуль, она остается без изменения, если нечетная — увеличивается на единицу. (Например, число 1234.50 округляют до 1234, а число 8765.50 — до 8766).
Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. (Например, число 6783.6 при сохранении четырех значащих цифр, округляют до 6784, а число 12.34520 — до 12.35).
Особенно внимательно следует относиться к записи результата измерения без указания погрешности, так как записи результата 2.4 10 3 В и 2400В не являются тождественными. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может находиться в интервале от 2.351кВ до 2.449кВ. Запись 2400 означает, что верны и единицы вольт, следовательно истинное значение напряжения может находиться в интервале от 2399.51В до 2400.49В.
Поэтому запись результата без указания погрешности крайне нежелательна.
Окончательно правила записи результата измерений можно сформулировать следующим образом.
1) При промежуточных вычислениях значения погрешности сохраняют три -четыре значащие цифры.
2) Окончательное значение погрешности и значение результата округляются в соответствии с изложенными выше правилами.
3) При однократных технических измерениях когда учитывается только основная погрешность СИ (СИ используются в нормальных условиях эксплуатации), результат записывается в виде:
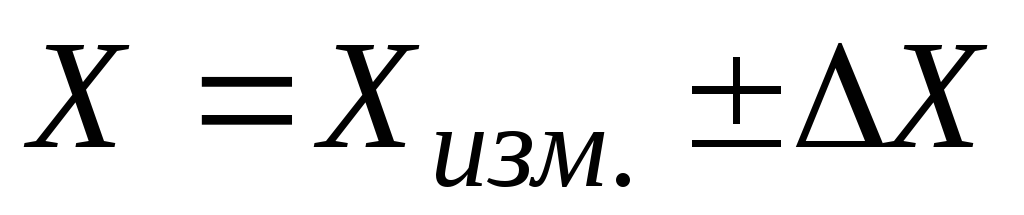
или
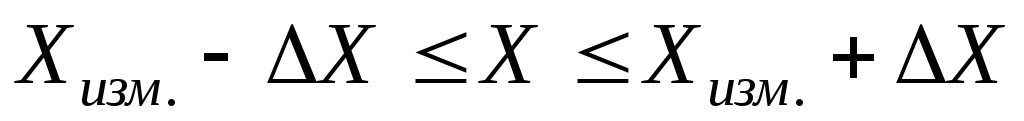
.
(Например, результат измерения напряжения 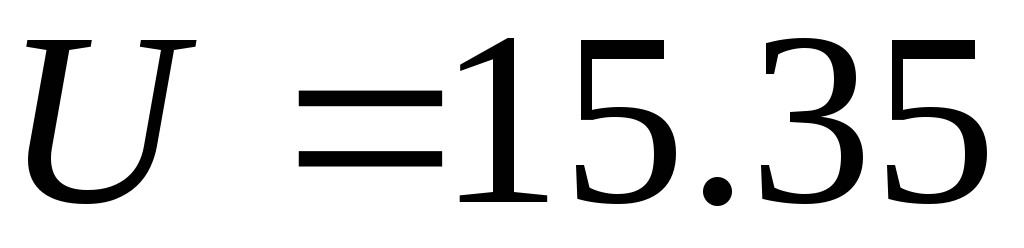 В, погрешность
В, погрешность 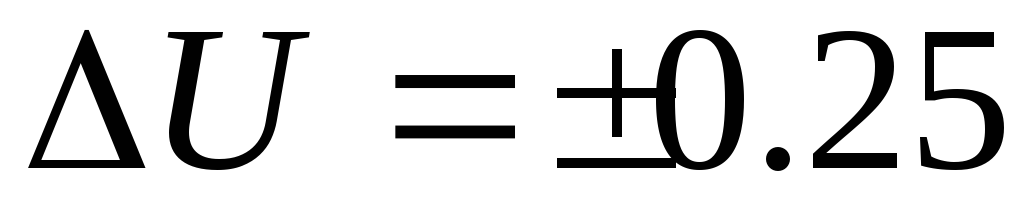 В. Результат может быть записан в виде:)
В. Результат может быть записан в виде:)
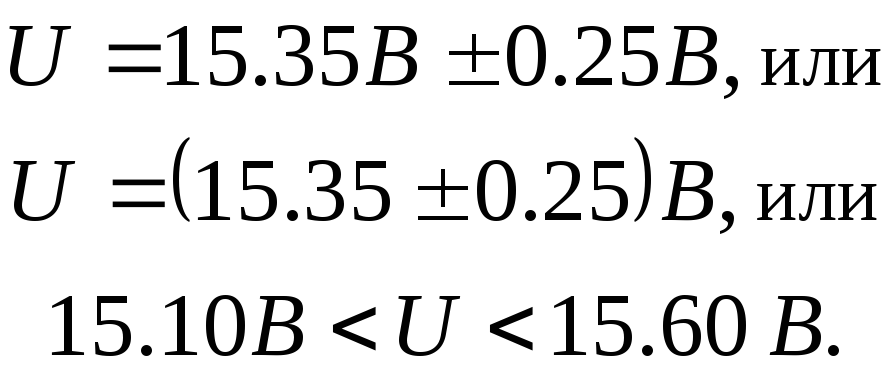
4) При однократных технических измерениях в рабочих условиях, когда по нормативным данным на СИ учитывают основную и дополнительные погрешности и результирующую погрешность определяют по формуле (1.35), результат записывают в виде:
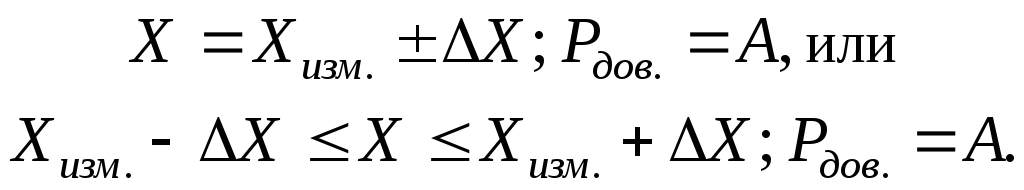
5) При статистических измерениях, когда определяется только величина случайной погрешности нормально распределенных данных в виде доверительного интервала, результат записывается в соответствии с (1.31):
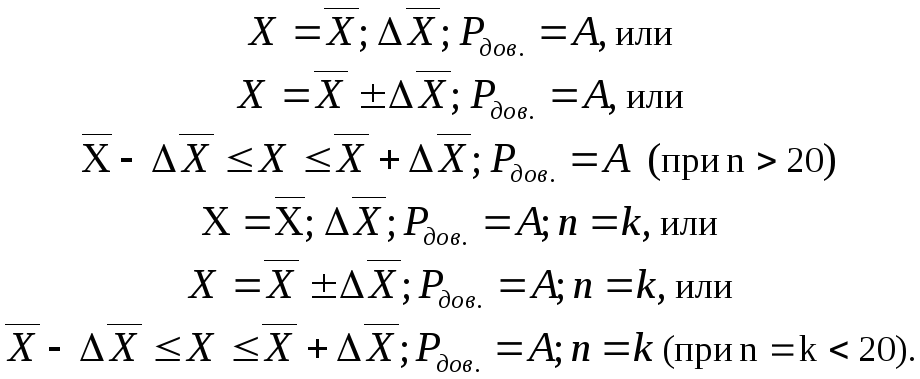
Если границы доверительного интервала несимметрична, то они указываются по отдельности.
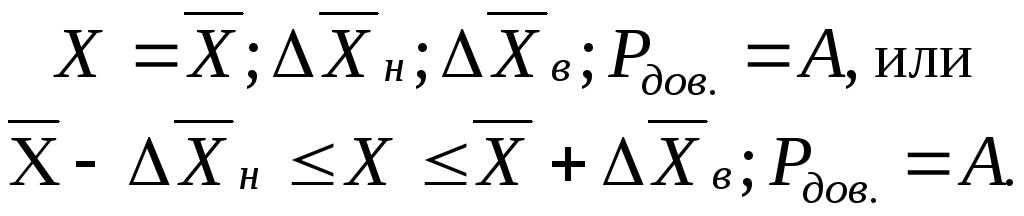
6) При статистических измерениях, когда оцениваются границы неисключенных систематических погрешностей результата (НСП) и доверительный интервал случайной погрешности нормально распределенных данных, но результат используется как промежуточный для нахождения других величин (например, при статистических косвенных измерениях) или предполагается сопоставление его с другими результатами аналогичного измерительного эксперимента, результат записывается в соответствии с (1.39):
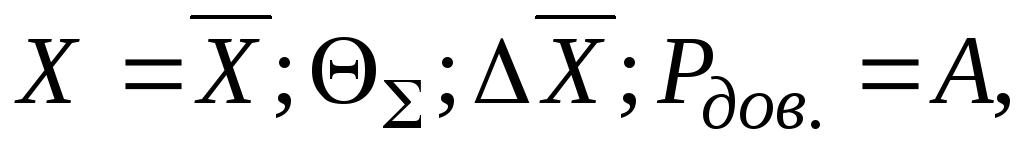
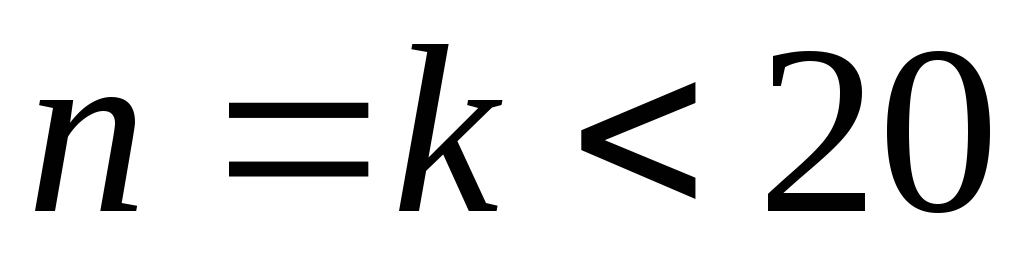
если , то это указывается дополнительно, как в п. 5.
Если границы НСП или границы доверительного интервала несимметричны, то они указываются по отдельности:
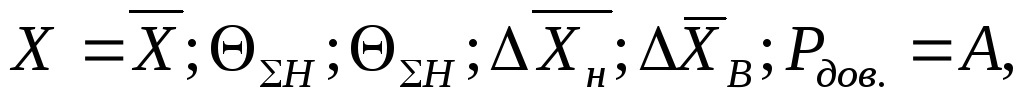
7) Если при измерении получены оценки погрешности при условиях, оговоренных в п. 6, но результат является окончательным и не предполагается в дальнейшем анализ его и сопоставление с другими результатами, то он записывается в соответствии с (1.41):
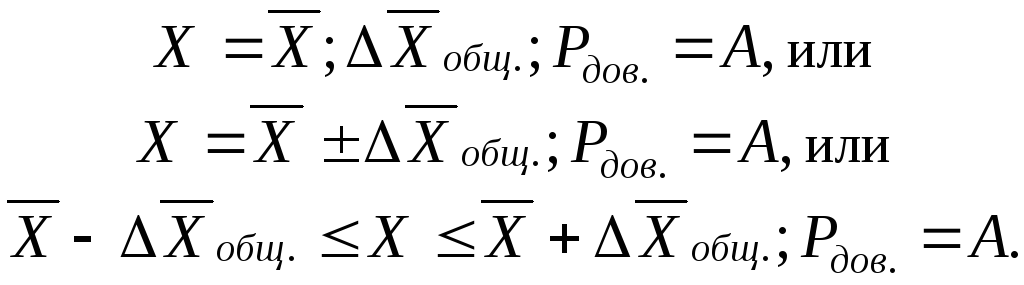

где определяется по формуле (1.40),
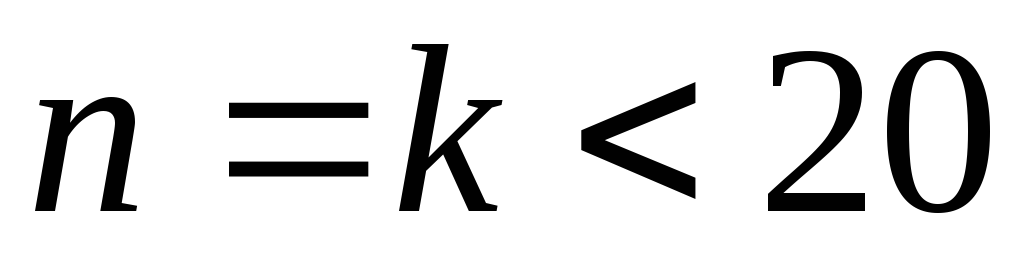
если же , это указывается дополнительно, как в п. 5.
8) При статистических измерениях, когда оцениваются границы НСП и доверительный интервал случайной погрешности, но при обработке результатов идентифицирован закон распределения, отличный от нормального, оценки значения результата измерения и доверительный интервал случайной погрешности находятся по соответствующим формулам [5], результат представляется в виде аналогичном представлению результата в п. 6, но дополнительно приводится информация о виде закона распределения опытных данных.
9) Если как в п. 8 обрабатываются результаты статических измерений и заранее известно, что закон распределения опытных данных отличается от нормального, но действий по идентификации вида реального закона по какой-либо причине не предпринимается, то результат может быть представлен в виде, аналогичном представлению результата в п. 6, но доверительный интервал случайной погрешности определяется в соответствии с рекомендациями ГОСТ 11.001-73 как 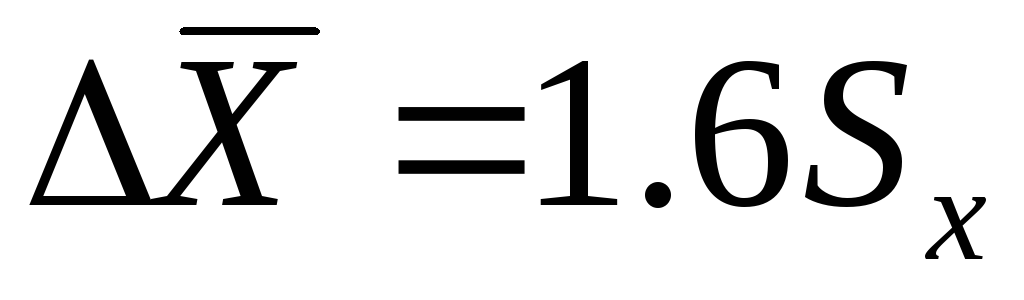 при доверительной вероятности
при доверительной вероятности 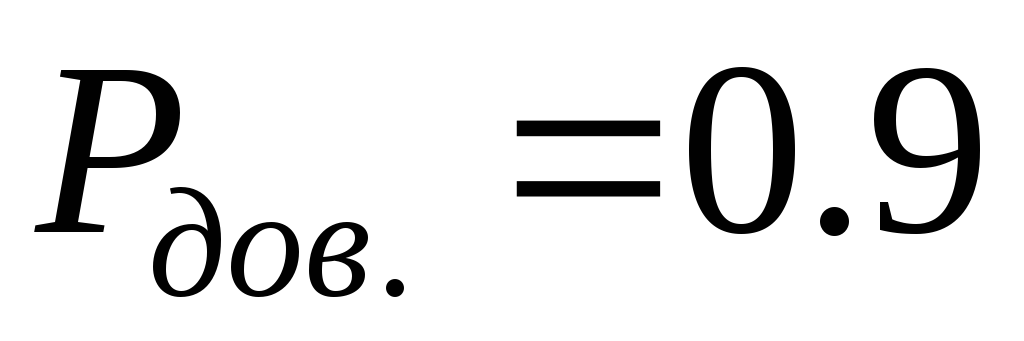 .
.
Запись результата может выглядеть, например, так:
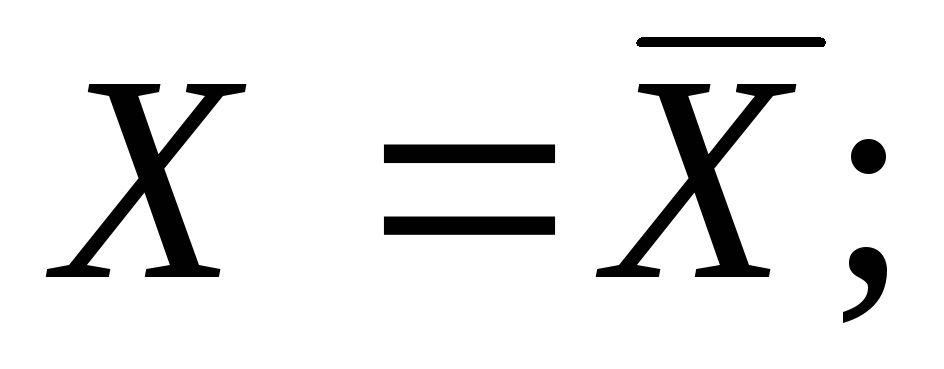
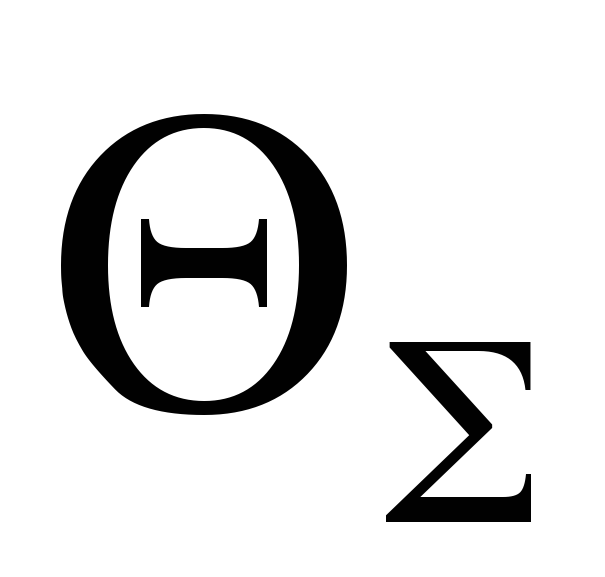 (при
(при 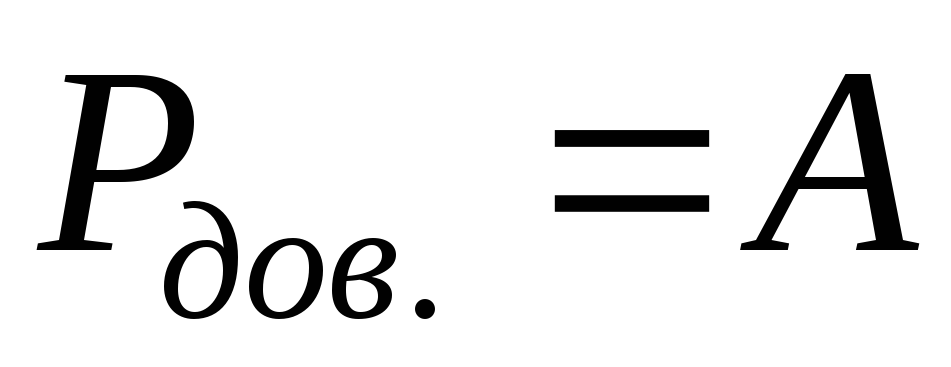 );
); 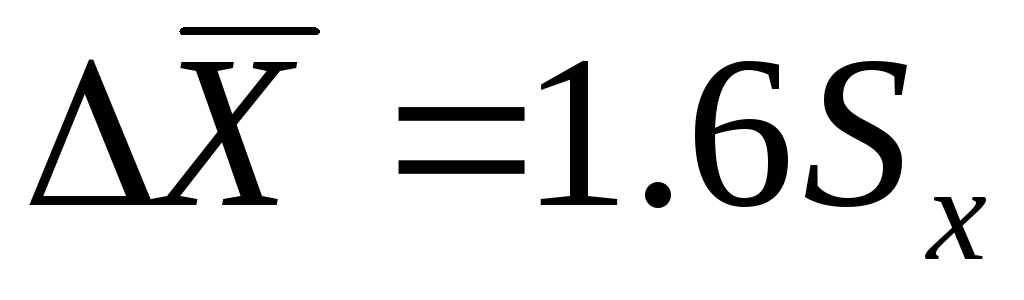 ;
; 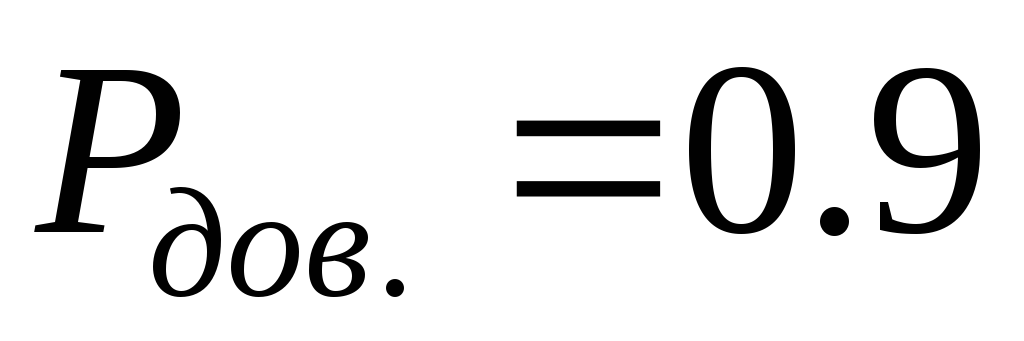 ;
; 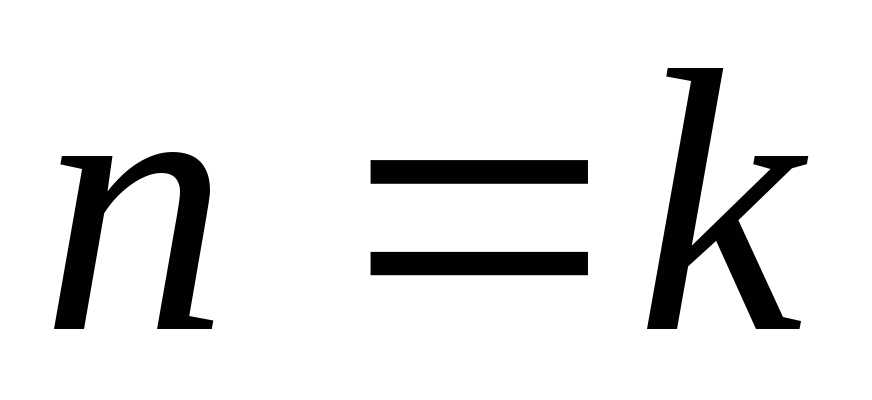 .
.
Доверительная вероятность, при которой определяется суммарный НСП — 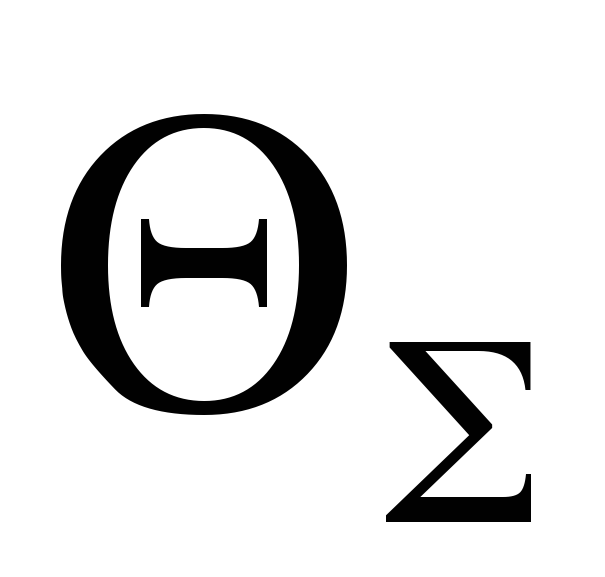 , в этом случае может отличаться от
, в этом случае может отличаться от 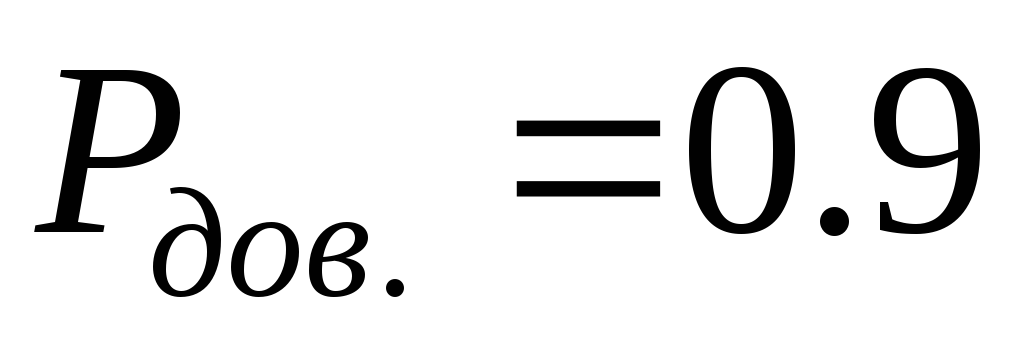 .
.
Источник: studfile.net