В настоящее время в системах управления ресурсами предприятия постоянно возникает потребность в создании и обработке триггеров, которые связаны с возникновением определенных событий в системе. Проблема, поставленная в данной работе, заключается в том, что существующие на данный момент ERP-системы не обладают достаточными возможностями для создания триггеров внутри системы для определенных задач предприятия, так как либо эти возможности ограничены определенным диапазоном объектов и действий, для которых можно создать триггер, либо такой функционал отсутствует и все триггеры должны устанавливаться при интеграции системы на предприятии и не могут быть впоследствии изменены. В связи с этим была разработана математическая модель алгоритма управления бизнес-процессами для ERP-систем, позволяющего настраивать триггеры внутри системы, а не при её интеграции. Исходя из разработанной математической модели, для создания триггеров в ERP-системах можно применять два способа: создание на уровне программного кода и создание на уровне базы данных. Использование данной модели обеспечивает уменьшение числа запросов на 52?%, а временных затрат на построение и обновление ERP-триггеров на 54?%.
Тихонов Н. А. — Основы математического моделирования — Типы математических моделей (Лекция 1)
ERP-системы
математическая модель
бизнес-процессы
быстродействие
1. Якунина А.В. Исследование теоретических подходов к управлению системами планирования ресурсов на предприятии // Актуальные проблемы гуманитарных и естественных наук. 2016. № 1–3. С. 182–184.
2. Кузнецов Л.А. Управление ресурсами предприятия // Надежность. 2005. № 3 (26). С. 37–42.
3. Павлов Д.В.
Триггеры в PLSQL // Аллея науки. 2016. № 4. С. 759–761.
4. Sliusar V.V., Nikolaev O.V., Dorogov V.G., Gagarina L.G., Andrianov A.M. Usage of triggers for business process controlling in ERP systems // Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2018-January, Р. 1567–1570. DOI: 10.1109/EIConRus.2018.8317398.
5. Михайлов А.А., Хмельнов А.Е. Метод визуализации графа потоков управления // Вестник Бурятского государственного университета. Математика, информатика. 2018. № 2. С. 50–62.
6. Шибанов С.В., Вишняков П.В., Лысенко Э.В., Смирнов Д.С., Орешкин К.А. Механизмы управления событиями в активных базах данных // Математическое и программное обеспечение систем в промышленной и социальной сферах. 2014. № 2 (5). С. 68–75.
7. Довбенко А.В. Идентификация изменений HTML-структур, приведенных к формату JSON // Наука, техника и образование. 2015. № 11 (17). С. 49–53.
8. Синдеев С.С. Исследование использования типа данных JSON в базе данных MYSQL // В сборнике: Фундаментальные и прикладные исследования: от теории к практике: материалы II международной научно-практической конференции, приуроченной ко Дню Российской науки. 2018. С. 201–204.
9. Портнов Е.М., Баин А.М., Чумаченко П.Ю. Методика разработки систем автоматизации бизнес-процессов предприятий // Оборонный комплекс – научно-техническому прогрессу России. 2011. № 2. С. 69–73.
Математическое моделирование — Лекция 1 (09.02.07)
10. Портнов Е.М., Баин А.М., Чумаченко П.Ю. Методика натурного моделирования распределенных автоматизированных систем управления бизнес-процессами предприятий // Оборонный комплекс – научно-техническому прогрессу России. 2010. № 4. С. 27–30.
В настоящее время управление предприятием непрерывно связано с использованием систем планирования ресурсов предприятия (ERP), которые позволяют автоматизировать процессы управления бухгалтерским учетом, инвентаризацией, менеджментом и другими отделами предприятия, интегрируя все это в одну систему [1, 2].
При работе в таких системах постоянно возникает потребность в выполнении определенных действий при наступлении некоторых событий, т.е. триггеров (например, добавление товаров в систему учета при поступлении их на склад). В большинстве ERP-систем настройка триггеров происходит отдельно для каждого предприятия при интеграции системы, связана с большими временными и финансовыми затратами и не может быть в дальнейшем использована при интеграции системы на других предприятиях.
Ниже приведен пример запроса для создания триггера на языке SQL, который добавляет в таблицу values запись об изменении таблицы example:
CREATE OR REPLACE TRIGGER ExampleUpdatedTrigger
AFTER UPDATE ON example
insert into info values (‘table «example» has changed’);
При появлении новых бизнес-процессов на предприятии добавление в ERP-систему новых триггеров также требует отдельной настройки системы и связано с дополнительными затратами, а существующие в системе триггеры, объекты триггеров или действия, исполняемые триггерами при вызове, не могут быть изменены или расширены, либо их модификация ограничена возможностями системы [3, 4].
Цель исследования: повышение быстродействия процессов построения и вызова триггеров управления бизнес-процессами предприятия в ERP-системах.
Материалы и методы исследования
Разработаем математическую модель триггеров ERP-системы и представим триггерные связи, возникающие при создании, изменении и удалении объектов ERP-системы, в виде графов – графа потока управления CFG и графа зависимостей DFG.
Триггер в рамках ERP-системы – это совокупность T множества событий системы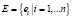 
и набора действий 
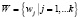. При возникновении любого события ei из множества E триггер T запускает по очереди действия wj из набора W. Каждое событие 
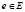в ERP-системе связано с объектом x системы и представляет собой изменение, создание, удаление объекта x или его атрибутов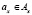 
Возникновение события задается функцией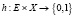 
, для которой h (e, x) = 1, если объект x был изменен, и 0 в остальных случаях. Действия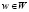 
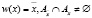(изменение объекта x, в результате которого часть атрибутов объекта изменяется); 
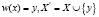(создание нового объекта y); 
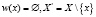(удаление объекта x); w(x) = x (действие, не изменяющее объект x).
Таким образом, триггер можно задать с помощью формулы
,
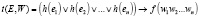
где e1, e2, en – события триггера, w1, w2, wn – действия триггера, f: 2W – функция, равная 1 в случае успешного выполнения последовательности действий w = w1 w2… wn = 1, и 0 в случае неудачи.
Для отображения триггерных связей между объектами ERP-системы удобно воспользоваться графовыми структурами, такими, как граф потока управления и граф зависимостей [5, 6].
Граф потока управления представляет собой совокупность CFG(V, T), где V = – множество действий над объектами ERP-системы, а T = – множество триггерных связей между объектами ERP-системы (рис. 1). В графе потока управления каждый узел (вершина) графа соответствует базовому блоку – прямолинейному участку кода, не содержащему в себе ни операций передачи управления, ни точек, на которые управление передается из других частей программы.
Имеется лишь два исключения:
− точка, на которую выполняется переход, является первой инструкцией в базовом блоке;
− базовый блок завершается инструкцией перехода.
Направленные дуги используются в графе для представления инструкций перехода. Также, в большинстве реализаций добавлено два специализированных блока:
− входной блок, через который управление входит в граф;
− выходной блок, который завершает все пути в данном графе. Блок, не связанный со входным блоком, считается недостижимым («мёртвый» код).
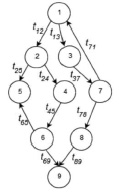
Рис. 1. Граф потока управления CFG в ERP-системе
Недостижимый блок может быть удален из программы. Блок, не связанный с выходным блоком, содержит бесконечный цикл. Полагаясь на это утверждение, удаётся обнаружить не все бесконечные циклы в связи с проблемой останова.
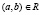
Пусть дано множество V = объектов ERP-системы и отношение транзитивности над этим множеством R = V×V, где следует зависимость для вычисления a нужно сначала вычислить b.
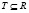
Тогда граф зависимостей представляет собой совокупность множеств DFG(V, T), где и R – транзитивное замыкание T (рис. 2).
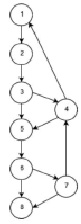
Рис. 2. Граф зависимостей DFG в ERP-системе
Формализация задачи построения триггеров в ERP-системе состоит из двух критериев [7]. Данные критерии представляют собой оценку быстродействия алгоритма построения триггеров в ERP-системе.
Пусть T(n), определенная как функция над графом CFG(V, T)
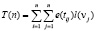
, (1)
где e(tij) – время на создание триггерной связи tij = (vi, vj), l(vj) – время на выполнение действий триггера над объектом j, представляет собой временные затраты на создание триггерных связей между объектами ERP-системы при накладываемых ограничениях.
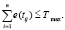
(2)
Тогда первый критерий быстродействия триггерного алгоритма
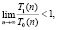
(3)
где T0 – временные затраты на создание триггерных связей до применения предложенной в данной работе методики; T1 – временные затраты на создание триггерных связей после применения данной методики.
2. Пусть D(n) – определенная как функция над графом DFG(V, T)
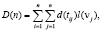
(4)
где d(tij) – задержка возникновения триггерной связи, возникающая при конфликте по данным (RAW, WAR). Тогда второй критерий быстродействия триггерного алгоритма – критерий быстродействия обновления графа триггеров при наличии конфликтов по данным:
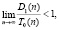
(5)
где D0 – временные затраты на обновление графа вызова триггеров до применения предложенной в данной работе методики; D1 – временные затраты на обновление графа вызова триггеров после применения данной методики.
Результаты исследования и их обсуждение
Исходя из разработанной математической модели, для создания триггеров в ERP-системах можно применять два способа: создание на уровне программного кода и создание на уровне базы данных. На основе данной модели была разработана методика построения триггеров управления бизнес-процессами в ERP-системах.
На первом этапе в отношении любой ERP-системы необходимо определить набор общих стандартных моделей (например, моделей организации), объектов (например, планы и списки поставщиков) и процессов (например, управление заказами).
Если ранее для каждого предприятия нужно было учитывать существующую на ней структуру и организацию данных, то при использовании ERP-системы необходимым и достаточным является использование одних и тех же моделей для каждой организационной единицы [7, 8]. Качество выбранных моделей оказывает огромное влияние на общий успех интеграции ERP-системы на предприятии.
В рамках языка программирования событие – это сообщение, которое возникает в различных точках исполняемого кода при выполнении определённых условий. Для решения поставленной задачи создаются обработчики событий: как только программа попадает в заданное состояние S, т.е. как только произойдет изменение, создание или удаление соответствующего объекта ERP-системы, происходит событие, посылается сообщение, а обработчик перехватывает это сообщение и выполняет действия w1, w2,…, wn∈W.
В общем случае в обработчик не передаётся ничего, либо передаётся ссылка на объект, инициировавший (породивший) обрабатываемое событие. В особых случаях в обработчик передаются значения некоторых переменных или ссылки на какие-то другие объекты, чтобы обработка данного события могла учесть контекст возникновения события. Таким образом, создание триггера на уровне программного кода позволяет запускать любые действия при вызове их обработчиков.
Аналогично, как и в случае обработчиков событий, как только база данных перейдет в состояние S, при котором произойдет изменение каких-либо объектов x ERP-системы, запускается хранимая процедура, соответствующая измененным объектам, и исполняются действия w1, w2,…, wn∈W. Однако в связи с тем, что внутри хранимой процедуры в БД можно указывать только действия, связанные с БД, то такой способ построения триггеров не дает возможности исполнять действия триггера вне базы данных [6].
Объединив два перечисленных способа, в работе применяется смешанный подход, состоящий в хранении триггера в сериализованном виде в базе данных, что одновременно обеспечивает и портируемость созданных ERP-триггеров, и возможность задавать любые действия, выполняемые при вызове триггера. При создании триггера все запросы к БД и другие действия в ERP-системе сериализуются и помещаются в БД. При вызове триггера данные десериализуются, оттуда извлекаются и запускаются действия триггера [9, 10].
Из построенной модели триггеров следует, что при вызове триггера могут изменяться данные объектов, использующиеся при вызове других триггеров. Такая ситуация может произойти, если в результате действий w∈W множество изменяемых объектов Xc пересекается c множеством объектов событий XЕ:
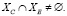
(6)
При этом могут возникать конфликты по данным [10]:
1. Read after Write (RAW). Триггер TA записывает значение в переменную, которую использует триггер TВ.
2. Write after Read (WAR). Триггер TA считывает значение переменной, в которую записывает новое значение триггер TВ.
3. Write after Write (WAW). Оба триггера записывают значения в одну и ту же переменную.
Чтобы избежать появления конфликтов по данным, применяется метод топологической сортировки графа триггеров с помощью обхода графа в глубину, который обеспечивает обновление графа зависимостей триггерных связей (рис. 3).
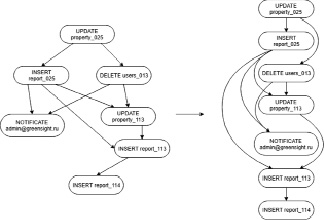
Рис. 3. Топологическая сортировка графа ERP-триггеров
Для оценки быстродействия разработанных методики и алгоритмов были проведены испытания по построению графа ERP-триггеров в системе планирования ресурсов предприятия Greensight ERP.
В качестве критериев быстродействия применялись следующие:
1. Временные затраты на создание триггерных связей между объектами
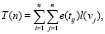
(7)
где e(tij) – время на создание триггерной связи tij = (vi, vj), l(vj) – время на выполнение действий триггера над объектом vj.
2. Временные затраты на обновление графа вызова ERP-триггеров при наличии конфликтов по данным
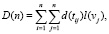
(8)
где d(tij) – задержка возникновения триггерной связи, возникающая при конфликте по данным (RAW, WAR), l(vj) – время на выполнение действий триггера над объектом vj.
В табл. 1 и 2 приведены результаты испытаний.
Быстродействие операций построения триггеров до применения разработанных алгоритмов
Источник: top-technologies.ru
ПРИНЯТИЕ РЕШЕНИЙ В БИЗНЕСЕ НА ОСНОВЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ Текст научной статьи по специальности «Экономика и бизнес»
В статье рассмотрены основы экономико-математического моделирования ; изучены этапы экономико-математического моделирования ; выявлены современные особенности применения экономико-математического моделирования в бизнесе.
i Надоели баннеры? Вы всегда можете отключить рекламу.
Похожие темы научных работ по экономике и бизнесу , автор научной работы — Бугаков С.С.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ КАК ФАКТОР ПОВЫШЕНИЯ КОНКУРЕНТОСПОСОБНОСТИ ПРЕДПРИЯТИЙ НА РЕГИОНАЛЬНОМ УРОВНЕ
АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ГОСТИНИЧНЫМ ПРЕДПРИЯТИЕМ В РОССИИ И ЗА РУБЕЖОМ: СРАВНИТЕЛЬНЫЙ АНАЛИЗ
ИНФОРМАЦИОННО-ТЕХНОЛОГИЧЕСКОЕ ПЕРЕВООРУЖЕНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ КАК ФАКТОР ПОВЫШЕНИЯ КОНКУРЕНТОСПОСОБНОСТИ
ИНФОРМАЦИОННО-ТЕХНОЛОГИЧЕСКОЕ ПЕРЕВООРУЖЕНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ КАК ФАКТОР ПОВЫШЕНИЯ КОНКУРЕНТОСПОСОБНОСТИ
Современные подходы к определению реинжинирига
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
i Надоели баннеры? Вы всегда можете отключить рекламу.
Текст научной работы на тему «ПРИНЯТИЕ РЕШЕНИЙ В БИЗНЕСЕ НА ОСНОВЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ»
ПРИНЯТИЕ РЕШЕНИЙ В БИЗНЕСЕ НА ОСНОВЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
В статье рассмотрены основы экономико-математического моделирования; изучены этапы экономико-математического моделирования; выявлены современные особенности применения экономико-математического моделирования в бизнесе.
Ключевые слова: системы поддержки принятия решений, экономико-математическое моделирование, информационные технологии.
Ни одно исследование в области экономики невозможно произвести без использования экономико-математического моделирования. Стремительное развитие математической статистики, исследования операций, математического анализа и теории вероятностей послужило катализатором формирования различных моделей экономики. [3]
Математически выраженные модели экономических процессов и явлений более емко можно охарактеризовать как экономико-математические модели. Классификация этих моделей производится на различны основаниях.
Экономико-математическое моделирование подразумевает процесс, направленный на выражение экономических явлений путем использования математических моделей. [9]
Экономическая модель — это схематичное представление экономического процесса или явления путем научной абстракции, отражение их характерных черт. Математические модели служат основным средством решения задач по оптимизации любой деятельности. Эти модели, по своей сути, являются средством плановых расчетов. [11] Ценность их для оптимизации решений и экономического анализа заключается в том, что с их помощью становится возможным определить лимитирующую группу оборудования, оценить напряженность плановых заданий, выявить виды ресурсов, получив оценку их дефицитности и т.д. Математическое моделирование экономических явлений и процессов позволяет получить четкую картину исследуемого объекта, охарактеризовать и количественно описать его внешние связи и внутреннюю структуру. [7]
Для этого экономико-математическая модель должна быть адекватной действительности, а также отражать существенные связи и стороны изучаемого объекта.
Экономико-математическое моделирование в бизнесе можно охарактеризовать как процесс применения математических методов в моделировании, прогнозировании, анализе и оптимизации управленческих, производственных, транспортных, логистических и иных экономических процессов. [2]
Применение экономико-математического моделирование в бизнесе позволяет упорядочить информационно-аналитическое обеспечение процессов управления.
Экономико-математическое моделирование, как и любое иное моделирование, основано на принципе аналогии, т.е. возможности не непосредственно изучения объекта, а через анализ иного, схожего с ним более доступного объекта. В рассматриваемом случае таковым более доступным объектом выступает экономико-математическая модель. [5]
По функциональному назначению экономико-математические модели подразделяются на два вида:
— теоретико-аналитические (используются при исследовании общих закономерностей и свойств экономических процессов);
— прикладные (применяются для решения конкретных экономических задач, модели прогнозирования, экономического анализа, управления).
Экономико-математическое моделирование при проведении экономических исследований все чаще используется в качестве одного из ключевых инструментов количественного анализа статистических данных о функционировании предприятия. Данное положение объясняется тем, что, математическое моделирование может служить в качестве эффективного средства более компактного и структурированного представления исходной информации. Помимо этого, существует целый ряд типичных управленческих ситуаций, допускающих формализацию, где именно математические соображения и подходы обоснованно становятся решающими. [8]
Вестник магистратуры. 2016. № 1(52). Т.3.
Современной особенностью применения экономико-математического моделирования в бизнесе является внедрение в данный процесс компьютерных информационных систем, в значительной степени стимулирующих развитие численных методов исследований в различных областях экономики, в том числе и в подсистемах поддержки принятия решений. Внедрение экономико-математического моделирования в процессы принятия обоснованных решений по управлению деятельностью предприятия позволяет получить существенные конкурентные преимущества для бизнеса. [1]
Сочетание современных компьютерных технологий и экономико-математических моделей позволяет производить комплексную оценку финансового состояния предприятия с достаточно высокой точностью и надежностью. [10]
Процессуально экономико-математическое моделирование происходит в несколько этапов.
На первом этапе производится определение характеристик рассматриваемого объекта, анализируется его реакция на всевозможные внешние воздействия, реализуется статистическая обработка полученных данных. Целью данного этапа является определение наиболее существенных, воздействующих на объект, факторов. Список существенных параметров, в процессе изучения объекта, может корректироваться. [4]
Второй этап построения экономико-математической модели заключается в ее спецификации. Происходит обнаружение связей и соотношений между переменными и параметрами выражающихся в математической форме.
Оценка параметров экономико-математической модели производится на основе определения их численных значений путем экономических экспериментов и статистических наблюдений. При этом она может быть интервальной либо точечной.
Разработка модели является итерационным процессом позволяющим уточнять и корректировать ее по мере изучения и использования. Так шаг за шагом происходит обеспечение адекватности создаваемой модели реальным процессам и объектам, действия которых она описывает. [6]
Подавляющее большинство современных математических алгоритмов и методов реализуются посредством стандартного программного обеспечения или специализированных пакетах прикладных программ. Это позволяет применять экономико-математические методы в бизнесе более активно и широко, что повышает эффективность и качество принимаемых решений при управлении предприятием в целом.
Внедрение новых математических методов приобретает особую актуальность в совершенствовании календарного планирования производственных процессов на предприятии. Как правило, эта задача заключается в распределении ограниченных ресурсов по операциям проекта.
Решение реальных задач календарного планирования основывается на двух подходах. [2]
Первый основан на внедрении эвристических алгоритмов. Одна группа алгоритмов оперирует определенными эвристическими правилами приоритетности операций при возникновении ситуаций, связанных с ограниченностью ресурсов. Другая группа использует идею улучшения некоторого начального решения, то есть локальной оптимизации.
Второй подход опирается на идею агрегирования, то есть сокращения количества операций проекта путем подмены нескольких операций на одну. Итоговый агрегированный проект, в силу меньших размеров, позволяет находить более эффективные методы решений. Конечным пунктом выступает дезагрегирование в календарный план исходного проекта полученного агрегированного решения. [5]
Использование инновационных математических моделей также является необходимым условием обеспечения конкурентоспособности компании, как на внутреннем, так и международном рынке. [2]
Не секрет, что существенным фактором успешной ценовой политики хозяйствующего субъекта на отдельно взятом рынке выступает не только установление ценовой политики в зависимости от устоявшейся стратегии и экспертная оценка конъюнктуры рынка, но и адекватная оценка как своих собственных издержек, так и издержек конкурентов.
Среди наиболее широко используемых методов выделяют следующие:
1) метод установления цены на основе издержек производства, в основе которого лежит измерение базовых издержек на единицу продукции, корректируемых на величину неучтенных затрат и норму прибыли предприятия. Данный способ соответствует затратному механизму формирования проектной цены;
2) метод безубыточности предполагает определение такого объема производства и реализации по заданной цене, который позволил бы покрыть переменные и постоянные издержки производства продукции без получения прибыли;
3) метод ориентации цены на уровень спроса на товар используется организациями, объем производства, для которых не имеет решающего значения. Они могут предельно приближать цены к возможностям потребителя;
4) конкурентный метод внешнеторгового ценообразования, который заключается в отборе фирмой представительской конкурентной информации на товарные аналоги с учетом различных условий взаи-
модействия предприятий конкурентов с потребителями.
В России метод ориентации цены на уровень спроса на товар и конкурентный метод внешнеторгового ценообразовании наиболее частое применяется в строительстве.
Наличие большого числа переменных чрезвычайно усложняет задачу принятия решения и возлагает на руководство компании немалую ответственность. Наиболее эффективным способом оценки всего множества факторов и степени их влияния здесь видится создание математической модели механизма прогнозирования с интеграцией методов эконометрики. [7]
Обобщая изложенный материал, необходимо отметить, что повсеместное широкое распространение высоких технологий открыло доступ к огромным объемам разнообразных данных. Потоки информации постоянно растут. Но чем больше информации собирается, тем сложнее увидеть в ней закономерности и тенденции, скрытые на первый взгляд.
Очень важно в этих условиях своевременно и быстро находить достоверную и полезную информацию, а также эффективно использовать ее. В современных условиях, практически невозможно достигнуть повышения конкурентоспособности случайным образом. Для этих целей необходима совокупность приемов и методов, позволяющих создавать инновационную систему управления конкурентоспособностью. Реализация такой системы напрямую связана с оценкой и анализом всего многообразия факторов и условий функционирования субъектов. Методы экономико-математического моделирования, область и возможности применения, которых существенно расширяются благодаря инновационным разработкам в сфере информационных технологий, можно без преувеличения назвать одним из наиболее динамично развивающихся разделов прикладной экономической науки.
1. Ашманов С.А. Введение в математическую экономику. — М.: Наука, 2014. — 210 с.
2. Кравченко Т.К. Математические и инструментальные методы экономики // Экономика. — 2013. — № 7. -С. 9-12.
3. Лотов А.В. Введение в экономико-математическое моделирование. — М.: Знание, 2010. — 284 с.
4. Морозов В.И. Математическое моделирование сложных аэроупругих систем. — М.: Физматлит, 2010. —
5. Попов А.Л. Системы поддержки принятия решений // Экономика. — 2010. — № 3. — С. 6-7.
6. Сайбель Н.Ю., Мезер С.Д. Теория оптимизации бизнес-процессов // Актуальные проблемы экономической теории и практики: сборник научных трудов. Выпуск 18. Краснодар: КубГУ, 2015. — С. 35-41.
7. Сайбель Н.Ю., Мезер С.Д. Оптимизация бизнес-процессов как инструмент повышения эффективности деятельности предприятия // Феномен рыночного хозяйства: от истоков до наших дней: материалы III-ой Международной научно-практической конференции / под ред. Я.С. Ядгарова, В.А. Сидорова, В.В.
Чапли. — Краснодар: Издательство НИИ экономики ЮФО, 2015. — С. 440-448.
8. Сайбель Н.Ю., Мезер С.Д. Оптимизация и реинжиниринг: сравнительный анализ // Молодой ученый. -2015. — № 13. — С. 453-456.
9. Сайбель Н.Ю., Мезер С.Д. Оптимизация бизнес-процессов как способ повышения конкурентоспособности бизнеса // Экономическое развитие России: системные ограничения и глобальные риски: материалы Международной научно-практической конференции. — Краснодар: Кубанский государственный университет, 2015. — С. 303-304.
10. Якушев А.А. Прогнозирование предпринимательской деятельности в торговой организации на основе современного экономико-математического инструментария // АПК: Регионы России. — 2012. — № 6. — С. 34-43.
11. Якушев А.А. Принятие управленческих решений на основе системного подхода и математического моделирования // Современные проблемы науки и образования. — 2014 — № 6. — С. 17-21.
БУГАКОВ СЕРГЕЙ СЕРГЕЕВИЧ — магистрант направления «Бизнес-информатика», Кубанский государственный университет, Россия.
Источник: cyberleninka.ru
Математическое моделирование в экономике — этапы, виды и использование
Моделирование в научных исследованиях использовалось с древних времен и постепенно охватило все новые отрасли науки: техническое проектирование, строительство и архитектура, астрономия, физика, химия, биология и, в конечном счете, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принесли метод моделирования в ХХ веке. Однако долгое время методология моделирования разрабатывалась самостоятельно отдельными науками. Не было единой системы понятий, единой терминологии. Лишь постепенно была признана роль моделирования как универсального метода научного познания.
Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие «модели», которые являются инструментами получения знаний.
Модель — это материальный или мысленно представленный объект, который заменяет собой первоначальный объект в процессе исследования, так что его непосредственное изучение дает новые знания о первоначальном объекте
Моделирование относится к процессу построения, исследования и применения моделей. Она тесно связана с такими категориями, как абстракция, аналогия, гипотеза и т.д. Процесс моделирования обязательно предполагает как построение абстракций и аналогий, так и построение научных гипотез.
Моделирование как метод научного познания
Главной особенностью моделирования является то, что оно является методом опосредованного познания с помощью суррогатных объектов. Модель функционирует как специальное средство познания, которое исследователь размещает между собой и объектом и с помощью которого исследует интересующий его объект. Именно эта особенность метода моделирования определяет конкретные формы использования абстракций, аналогий, гипотез, других категорий и методов познания.
Необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, связанные с ними) вообще нельзя изучать напрямую, или это исследование требует много времени и денег.
Процесс моделирования включает три элемента: 1) субъект (исследователь), 2) объект исследования, 3) модель, которая передает отношения между узнаваемым субъектом и узнаваемым объектом.
Объект A считается существующим или созданным. Мы строим (материально или ментально) или находим в реальном мире другой объект B — модель объекта A. Фаза создания модели предполагает наличие определенных знаний об исходном объекте. Познавательные возможности модели определяются тем, что модель воспроизводит все существенные особенности исходного объекта. Вопрос о необходимости и достаточной степени сходства оригинала и модели требует специального анализа. Очевидно, что модель теряет свой смысл как в случае идентичности с оригиналом (тогда она перестает быть оригиналом), так и в случае чрезмерного отклонения от оригинала во всех существенных отношениях.
Таким образом, изучение одних аспектов моделируемого объекта происходит за счет отказа от рассмотрения других аспектов. Поэтому любая модель заменяет оригинал только в строго ограниченном смысле. Из этого следует, что для объекта можно создать несколько «специализированных» моделей, ориентированных на конкретные стороны исследуемого объекта или характеризующих объект с различной степенью детализации.
На втором этапе процесса моделирования модель выступает в качестве самостоятельного объекта исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, в ходе которых намеренно изменяются условия работы модели и систематизируются данные о ее «поведении». Конечным результатом этого этапа является совокупность знаний о модели R.
Третья стадия предполагает перенос знаний из модели в оригинал, т.е. формирование совокупности знаний S об объекте. Этот процесс передачи знаний протекает по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств исходного объекта, которые не учитывались или не изменялись при построении модели. Мы можем обоснованно перенести любой результат от модели к оригиналу, если этот результат обязательно связан с особенностями сходства оригинала и модели. Однако, если определенный результат исследования модели связан с разницей между моделью и оригиналом, то этот результат непригоден для передачи.
Четвертый этап — практическая проверка знаний, полученных с помощью моделей, и их использование при построении обобщенной теории объекта, его трансформации или управления.
Чтобы понять суть моделирования, важно не упускать из виду тот факт, что моделирование — не единственный источник знаний об объекте. Процесс моделирования «встроен» в более общий процесс познания. Этот факт учитывается не только на этапе построения модели, но и на заключительном этапе, когда результаты исследований, полученные на основе различных когнитивных инструментов, объединяются и обобщаются.
Моделирование — это циклический процесс. Это означает, что за первым четырехступенчатым циклом могут последовать второй, третий и так далее. В то же время знания об изучаемом объекте становятся все более точными, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, вызванные плохим знанием объекта и ошибками при построении модели, могут быть исправлены в последующих циклах. Таким образом, методология моделирования предоставляет большие возможности для саморазвития.
Математическое моделирование — это изучение явлений и объектов в экономике с использованием математических моделей.
Этапы математического моделирования
Построение математических моделей состоит из нескольких этапов.
На первом этапе определяются задачи и разрабатывается концептуальная модель. Объект моделирования, его функциональное назначение, окружающая среда описываются устно, определяются отдельные элементы, свойства объекта, возможные состояния, идентифицируются связи между элементами. Такое предварительное представление объекта является концептуальной моделью.
На втором этапе происходит построение модели. На основе осмысленного описания объекта проводится анализ исходного набора характеристик объекта, идентифицируются важнейшие характеристики, определяются контролируемые и неконтролируемые параметры, вводятся их метки, создается система ограничений и строится объектная функция. Таким образом, результатом этого этапа является математическая модель объекта.
Следует учитывать, что простота модели зависит от выбора переменных. При составлении ограничений необходимо убедиться, что все условия ограничений присутствуют в модели.
На третьем этапе определяются метод и алгоритм решения. Тот или иной метод теории оптимального решения зависит от характера и структуры объективной функции и ее ограничений.
На четвертом этапе проверяется адекватность модели и, при необходимости, вносятся коррективы в модель. Верификация выражается в определении степени соответствия модели критериям практики, т.е. соответствия результатов наблюдений и теоретических последствий модели. На этапе монтажа могут потребоваться дополнительные исследования на месте. Подгонка математической модели может быть выполнена одним из трех способов:
- Расширение внешних факторов;
- Переход к более высокой степени нелинейности;
- Расширение списка ограничений.
На пятом этапе ведется поиск решений. После достижения удовлетворительного уровня адекватности модели используется соответствующий алгоритм для определения оптимального решения на модели.
На шестом этапе найденное решение реализуется на практике.
Математическая модель редко может быть выбрана из имеющихся моделей. Параметризация производится таким образом, чтобы модель соответствовала исследуемому объекту.
Виды математических моделей
Построение математических моделей в экономике осуществляется для достижения одной из перечисленных целей:
Теоретические модели используются для изучения общих закономерностей экономических систем, а также их свойств;
Прикладные модели создаются для разработки конкретных рекомендаций по практическим решениям и носят оптимизационный характер.
Все математические модели разделены:
- Макроэкономические, которые описывают экономику всего государства и связывают воедино агрегированные показатели: ВНП, НДП, инфляцию, занятость и др. Такие модели обычно носят теоретический характер.
- Микроэкономические модели, в которых моделируемая система является единой фирмой. Эти модели называются полуэмпирическими (смешанные модели).
На рисунке 1 показана общая картина экономического развития и роль математического моделирования в нем.
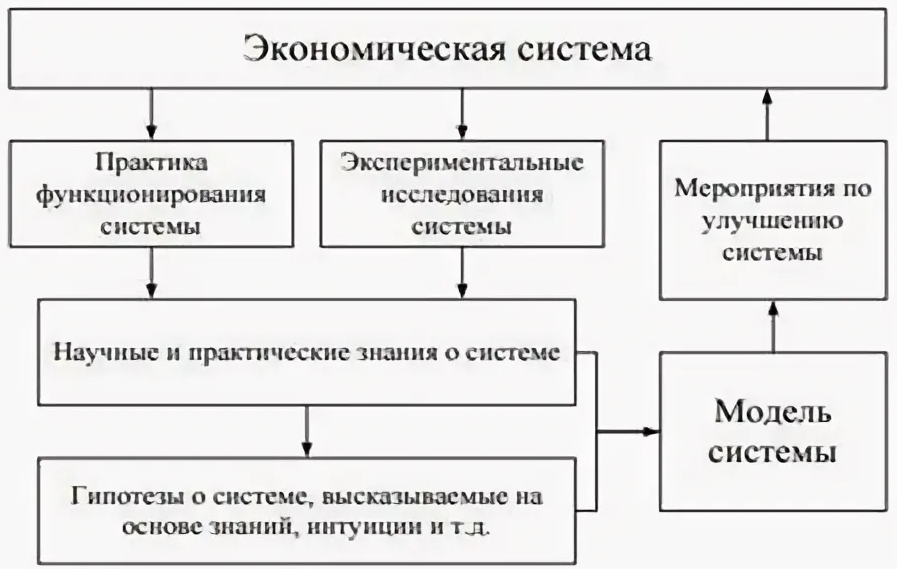
Рисунок 1: Роль моделирования в экономической системе.
При создании математических моделей в экономике необходимо учитывать, что многие свойства таких моделей нельзя точно определить, так как на их ценность сильно влияет «человеческий фактор». Поэтому свойства экономических моделей являются случайными переменными.
Экономические и математические модели являются в некоторой степени неопределенными. При теоретическом моделировании эта неопределенность остается за рамками исследований, в то время как при прикладном моделировании неопределенность должна приниматься во внимание. Всегда будет вероятность иного развития реальной ситуации, поэтому в модель необходимо встроить контрмеры или страховые меры для таких случаев.
Использование математического моделирования в бизнесе
Внедрение математических методов в экономику сопровождалось преодолением некоторых трудностей, связанных с развитием математики за счет потребностей физических и инженерных наук. Здесь главная причина скрыта в природе экономических процессов и самой экономической науке.
Многие объекты, изучаемые экономической наукой, могут быть охарактеризованы термином «сложная система».
Система — это набор элементов, которые взаимодействуют и формируют определенную целостность.
Важным свойством любой системы является возникновение, то есть наличие свойств, не присущих какому-либо элементу системы. Поэтому при изучении систем недостаточно разбивать их на элементы, а затем изучать. Так же и в экономических исследованиях — нет таких экономических объектов, которые можно было бы рассматривать как отдельные элементы.
Сложность системы зависит от количества ее элементов, их соединений, взаимоотношений системы и внешней среды. Например, экономика страны имеет все характеристики сложной системы, так как она сочетает в себе многие элементы, ее внутренние отношения разнообразны.
Сложность экономики в некоторых случаях являлась оправданием невозможности ее моделирования, исследований с использованием математики. Однако эта точка зрения оказалась ошибочной. Любой объект может быть смоделирован. И именно сложные объекты представляют наибольший интерес, потому что в этих условиях моделирование дает свои результаты.
Потенциальная вероятность математического моделирования в экономике не означает его успешного применения в той или иной ситуации. В экономической системе всегда существуют неформализованные проблемы и ситуации, когда математическое моделирование недостаточно эффективно.
- Экономическая теория
- Экономика
- Социально-экономические показатели безработицы — уровень и продолжительность безработицы
- Рынки электронной экономики — концепция, факторы и недостатки
- Идеи экономического либерализма — история возникновения, понятие, суть и концепция
- Теория эластичности спроса — виды и основы
- Виды производства — понятие и производство
- Промышленность Австрии — структура и особенности
- Методы исчисления ВНП — определение и различные методы
- Цели и задачи смешанной экономики — компоненты, суть и проблемы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник: www.evkova.org
