Моделирование проходит в 5 этапов.
Первый этап — постановка задачи включает в себя стадии: описание задачи, определение цели моделирования, анализ объекта.
Задача формулируется на обычном языке. По характеру постановки все задачи можно разделить на две основные группы. К первой группе можно отнести задачи, в которых требуется исследовать, как изменятся характеристики объекта при некотором воздействии на него, «что будет, если. ».
В задачах, относящихся ко второй группе, требуется определить, какое надо произвести воздействие на объект, чтобы его параметры удовлетворяли некоторому заданному условию, «как сделать, чтобы. ».
• Определение цели моделирования
На этой стадии необходимо среди многих характеристик (параметров) объекта выделить существенные.
• Например, если вы строите модель яхты для участия в соревнованиях моделей судов, то в первую очередь вас будут интересовать ее судоходные характеристики. Вы будете решать задачу «как сделать, чтобы…?»
Ошибки моделирования бизнес процессов в нотации BPMN
• А того, кто собирается на яхте в круиз, помимо тех же самых параметров, будет интересовать, внутреннее устройство: количество палуб, комфортабельность и т. п.
• Для конструктора яхты, строящего компьютерную имитационную модель для проверки надежности конструкции в штормовых условиях, моделью яхты будет изменение изображения и расчетных параметров на экране монитора при изменении значений входных параметров. Он будет решать задачу «что будет, если…?»
Определение цели моделирования позволяет четко установить, какие данные являются исходными, что требуется получить на выходе и какими свойствами объекта можно пренебречь.
Таким образом, строится словесная модель задачи.
***Анализ объекта подразумевает четкое выделение моделируемого объекта и его основных свойств.
Второй этап — формализация задачи связан с созданием формализованной модели, то есть модели, записанной на каком-либо формальном языке. Например, данные переписи населения, представленные в виде таблицы или диаграммы — это формализованная модель.
Формализация — это приведение существенных свойств и признаков объекта моделирования к выбранной форме.
Формальная модель — это модель, полученная в результате формализации.
Для решения задачи на компьютере больше всего подходит язык математики. В такой модели связь между исходными данными и конечными результатами фиксируется с помощью различных формул, а также накладываются ограничения на допустимые значения параметров.
Третий этап — разработка компьютерной модели начинается с выбора инструмента моделирования, другими словами, программной среды, в которой будет создаваться и исследоваться модель.
От этого выбора зависит алгоритм построения компьютерной модели, а также форма его представления. В среде программирования это программа, написанная на соответствующем языке. В прикладных средах (электронные таблицы, СУБД, графических редакторах и т. д.) это последовательность технологических приемов, приводящих к решению задачи.
Введение в BPMN. Часть 1. Основные элементы
Следует отметить, что одну и ту же задачу можно решить, используя различные среды. Выбор инструмента моделирования зависит, в первую очередь, от реальных возможностей, как технических, так и материальных.
Четвертый этап — компьютерный эксперимент включает две стадии: тестирование модели и проведение исследования.
Тестирование модели — процесс проверки правильности построения модели.
На этой стадии проверяется разработанный алгоритм построения модели и адекватность полученной модели объекту и цели моделирования.
Для проверки правильности алгоритма построения модели используется тестовые данные, для которых конечный результат з а р а н е е и з в е с т е н. (Обычно его определяют ручным способом). Если результаты совпадают, то алгоритм разработан верно, если нет — надо искать и устранять причину их несоответствия.
Тестирование должно быть целенаправленным и систематизированным, а усложнение тестовых данных должно происходить постепенно. Чтобы убедиться, что построенная модель правильно отражает существенные для цели моделирования свойства оригинала, то есть является адекватной, необходимо подбирать тестовые данные, которые отражают реальную ситуацию.
К этой стадии компьютерного эксперимента можно переходить только после того, как тестирование модели прошло успешно, и вы уверены, что создана именно та модель, которую необходимо исследовать.
Пятый этап — анализ результатов является ключевым для процесса моделирования. Именно по итогам этого этапа принимается решение: продолжать исследование или закончить.
Если результаты не соответствуют целям поставленной задачи, значит, на предыдущих этапах были допущены ошибки. В этом случае необходимо корректировать модель, то есть возвращаться к одному из предыдущих этапов. Процесс повторяется до тех пор, пока результаты компьютерного эксперимента не будут отвечать целям моделирования.
- JS
- Компьютерная графика
- Комп Графика
- Моделирование
- 1.Понятие моделирования. История развития математического моделирования. Особенности компьютерного моделирования.
- 2.Основные этапы процесса моделирования. Специфика процесса клмпьютерного моделирования.
- 3.Понятия содержательной модели, математической модели. Постулаты. Параметры и характеристики моделей. Свойства моделей.
- 4.Классификация моделей.
- 5.Понятие технической системы, её элементов, комплекса, свойств и т.д. Классы моделей, используемые при моделировании технических систем.
- 6.Системы и сети массового обслуживания. Основные понятия и приёмы моделирования для СМО.
- 7.Аналитические модели СМО.
- 8.Понятие случайного процесса. Марковские цепи и процессы.
- 9.Примеры моделей на основе марковских цепей и процессов. Эргодическое свойство.
- 10.Имитационное моделирование. История, принципы, примеры.
- 11.Структурные и функциональные модели. Программирование как моделирование.
- 12.Развитие программирования как одного из вариантов моделирования. Объектно-ориентированное моделирование, проектирование и программирование.
- 13.Принципы объектно-ориентированного программирования.
- 14.Язык Java ООП. Особенности ООП в Java.
- 15.Полиморфизм в ООП.
- 16.Примеры объектно-ориентированного подхода к проектированию программных систем.
Источник: ek-ek.jimdofree.com
Определите порядок выполнения этапов бизнес моделирования
Информационное моделирование – это творческий процесс. Не существует универсального рецепта построения моделей , пригодного на все случаи жизни, но можно выделить основные этапы и закономерности, характерные для создания самых разных моделей.
Первый этап – постановка задачи. Прежде всего следует уяснить цель моделирования . Исходя из цели моделирования, определяется вид и форма представления информационной модели , а также степень детализации и формализации модели. В соответствии с целью моделирования заранее определяются границы применимости создаваемой модели. На этом этапе также необходимо выбрать инструментарий, который будет использоваться при моделировании (например, компьютерную программу ).
Второй этап – собственно моделирование, построение модели. На этом этапе важно правильно выявить составляющие систему объекты , их свойства и взаимоотношения и представить всю эту информацию в уже выбранной форме. Создаваемую модель необходимо периодически подвергать критическому анализу, чтобы своевременно выявлять избыточность , противоречивость и несоответствие целям моделирования.
Третий этап – оценка качества модели, заключающаяся в проверке соответствия модели целям моделирования. Такая проверка может производиться путем логических рассуждений, а также экспериментов, в том числе и компьютерных. При этом могут быть уточнены границы применимости модели. В случае выявления несоответствия модели целям моделирования она подлежит частичной или полной переделке.
Четвертый этап – эксплуатация модели, ее применение для решения практических задач в соответствии с целями моделирования.
Пятый этап – анализ полученных результатов и корректировка исследуемой модели.
Источник: www.sites.google.com
Последовательность процесса моделирования;
Построение математической модели системы включает несколько этапов (рис. 1.2).

Рис. 1.2. Схема процесса моделирования
Этап 1. Постановка задачи. Этапу постановки задачи предшествует возникновение каких-либо ситуаций или проблем, осознание которых приводит к необходимости их обобщения или решения для последующего достижения какого-либо эффекта. Исходя из этого, объект подвергается всестороннему рассмотрению, отмечаются вопросы, подлежащие решению, и ставится цель исследования. На этом этапе необходимо уяснить, что мы хотим получить в результате исследований, а также предварительно оценить, нельзя ли получить эти результаты другим путем.
Этап 2. Определение задачи и построение концептуальной модели. Исследователь старается определить, к какому виду относится объект, описывает параметры состояния объекта, переменные, характеристики, факторы внешней среды. Необходимо понять закономерности внутренней организации объекта, построить его структуру, т.е. идентифицировать систему. Исходя из этого, выбирается задача исследования, которая позволит решить вопросы оптимизации, сравнения, оценки, прогноза, анализа чувствительности, выявления функциональных соотношений и т.д.
Последующая работа связана с разработкой сценария функционирования объекта и разработкой концептуальной модели. Например, для структуры общеэкономического баланса концептуальная модель (рис. 1.3) строится следующим образом.

Рис. 1.3. Схема концептуальной модели экономической деятельности
Со стороны предприятий на рынок конечных продуктов и услуг поступает поток товаров q, измеряемый для каждого отдельного вида товара в единицах продукции на единицу времени (ед./год). В соответствии со складывающимися на рынке ценами Р (руб./ед.), расходами домашних хозяйств С(руб./год) и правительства G (руб./год) поток расходов движется навстречу потоку товаров. Расходы правительства G включают оплату труда работников госучреждений и финансирование госзаказов предприятиям. Совместно с потоком инвестиций I (руб./год) потоки С и G образуют главную часть дохода бизнеса, другой составляющей доходов бизнеса является экспорт E (руб./год) за вычетом импорта М (руб./год), то есть результирующее сальдо Х= Е – М.
Поток; суммарных доходов бизнеса

отражает так называемую структуру валового национального продукта (ВНП). Структура ВНП как совокупного потока доходов бизнеса имеет вид
YВНП = С+ G+ I+(Е-М), а структура валового потока доходов домашних хозяйств –
YВНП =С+S+T; S – накопления; Т – налоги
Из концептуальной модели макроэкономический баланс опре-1ется фундаментальным уравнением Д. Кейнса:
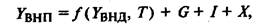
где f(YВНП, Т) – функция потребления домашнего хозяйства.
Необходимость проведения исследования возникает из реальных ситуаций, складывающихся в процессе работы систем, когда они в чем-либо начинают не удовлетворять каким-либо требованиям. Если недостатки очевидны и известны методы их устранения, нет необходимости в исследованиях.
К сожалению, такая ситуация встречается достаточно редко. В силу сложности систем и достаточно большого числа факторов, влияющих на эффективность функционирования, поставить «диагноз» системе не всегда просто. Изучение сложившейся ситуации, поведения системы и ее элементов, опыт исследователя и его интуиция позволяют сделать предварительный диагноз системе, определить и сформулировать задачу исследования.
Исходя из задачи исследования, определяется назначение математической модели, которая должна быть построена. Такие модели могут решать задачи:
• выявления функциональных соотношений — определение количественных зависимостей между входными факторами модели выходными характеристиками исследуемого объекта;
• анализа чувствительности — установление из множества факторов, действующих на систему, тех, которые в большей степени влияют на интересующие исследователя выходные характеристики;
• прогноза — определение поведения системы при некотором предполагаемом сочетании внешних условий;
оценки — определение того, насколько хорошо исследуемый объект будет соответствовать некоторым критериям;
• сравнения — сопоставление ограниченного числа альтернативных вариантов систем или же сопоставление нескольких предлагаемых принципов или методов действия;
• оптимизации — точное определение такого сочетания переменных управления, при котором обеспечивается экстремальное
значение целевой функции.
Выбор задачи определяет процесс конструирования и экспериментальной проверки модели.
Любое исследование должно начинаться с построения плана, включающего обследование системы и анализ ее функционирования. В плане предусматривается:
• описание функций, реализуемых объектом;
• определение взаимодействий всех систем и элементов объекта;
• определение зависимостей между входными и выходными переменными и влияния переменных управляющих воздействий на эти зависимости;
• определение экономических показателей функционирования системы.
Результаты обследования системы и окружающей среды представляются в виде описания процесса функционирования, которое используется для идентификации системы.
Идентифицировать систему — значит выявить и изучить ее, т.е. получить возможно более полную характеристику системы и ее поведения, познать объективные закономерности ее внутренней организации, очертить ее границы, указать на вход, процесс и выход, определить налагаемые на них ограничения, построить структурную и математическую модели, описать на каком-либо формальном абстрактном языке, определить цели, принуждающие связи, критерии действия системы.
После идентификации системы строится концептуальная модель, являющаяся «идеологической» основой будущей математической модели. Именно в ней отражается состав критериев оптимальности и ограничений, определяющих целевую направленность модели. Перевод на этапе формализации качественных зависимостей в количественные преобразует критерий оптимальности в целевую функцию, ограничения — в уравнения связи, концептуальную модель — в математическую. Концептуальная модель (рис. 1.4) на заключительном этапе ее построения проверяется на адекватность исследуемой системы реальной.
Схема построения концептуальной модели позволяет понять, что процесс ее построения представляет собой не только прямую, но и обратную связь отдельных этапов. Это означает, что при работе над последующим этапом приходится возвращаться к предыдущим для уточнения тех или иных моментов.
Для построения концептуальной модели производственно-экономическую систему рассматривают как кибернетическую систему с указанием основных и обратных связей, входа и выхода и подсистем управления.

Рис. 1.4. Концептуальная модель функционирования производственной системы
На основе концептуальной модели можно построить факторную модель (рис. 1.5), которая устанавливает логическую связь между параметрами объекта, входными и выходными переменными, факторами внешней среды и параметрами управления. При этом также учитываются обратные связи в системе.

Этап 3. Составление математической модели. Вид математической модели в значительной степени зависит от цели исследования. Вначале лучше поискать подходящую модель в литературе или использовать те или иные известные закономерности экономики в виде функций, связывающих переменные и постоянные факторной модели между собой: Математическая модель может быть представлена в виде математического выражения — алгебраического уравнения или неравенства, не имеющих разветвления вычислительного процесса при определении любых переменных состояния модели, целевой функции и уравнений связи. Для построения такой модели формулируются следующие понятия: критерий оптимальности, целевая функция и ограничения. Так, например, для факторной модели (рис. 1.5) выбираем в качестве ограничений значения переменных X, Р и Qвх, тогда Целевая функция будет иметь вид
Y = f (X, A, S, F)
а функция оптимизации —
Y = ext f (X, A, S, F)
Следующими этапом построения математической модели системы является формирование математической модели, включающее в себя несколько видов работ: математическую формализацию, численное представление, анализ модели и выбор метода ее решения.
Математическая формализация осуществляется по концептуальной модели. При формализации рассматриваются три основные ситуации:
1. Известны уравнения, описывающие поведение объекта. В этом случае решение прямой задачи позволяет найти реакцию объекта на заданный входной сигнал.
2. Обратная задача, когда по заданному математическому описанию и известной реакции необходимо найти входной сигнал, вызывающий этот отклик.
3. Математическое описание объекта неизвестно, но имеются или могут быть заданы совокупности входных и соответствующих им выходных сигналов. В этом случае имеем дело с задачей идентификации объекта.
При моделировании производственно-экономических объектов в третьей ситуации (при решении задачи идентификации) используется подход, предложенный Н. Винером, известный как метод «черного ящика». В качестве «черного ящика» рассматривается объект в целом вследствие его сложности. Так как внутреннее устройство объекта неизвестно, мы можем изучить «черный ящик», изучая входы и выходы. Сопоставляя вход и выход, можно записать уравнение
X — вектор входных параметров;
Y — вектор выходных параметров;
А — оператор объекта, преобразующий входные параметры в выходные.
Для описания объекта в виде математической зависимости в задачах идентификации используются методы регрессионного анали-1. При этом возможно описание объекта множеством математических моделей, так как нельзя вывести обоснованного суждения о |его внутреннем устройстве.
При развитой системе математического обеспечения ЭВМ целый ряд процедур моделирования осуществляется с помощью стан-1ртных программ. Оригинальные математические модели можно построить на основе проведенных исследований систем, апробированных в ходе производства. Для проведения новых исследований 1е модели корректируются под новые условия. Математические модели элементарных процессов, физическая природа которых известна, записываются в виде тех формул и зависимостей, которые установлены для этих процессов. Как правило, статические задачи записываются в виде алгебраических выражений, динамические — в виде дифференциальных или конечно-разностных уравнений.
При моделировании широко используются методы преобразования табличных значений к аналитическому виду с помощью интерполяции, аппроксимации и экстраполяции.
Интерполяция – приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же или другой величины, с ней связанной. Например, через любые n + 1 точек можно всегда провести линию, описываемую полиномом n-ой степени так, чтобы она прошла через каждую из заданных точек. Полученная линия называется интерполирующей функцией и может быть получена методом Лагранжа или Ньютона.
Аппроксимация — замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов.
Экстраполяция функции — продолжение функции за пределы ее области определения, при котором продолженная функция принадлежит заданному классу.
Экстраполяция функции обычно производится с помощью формул, в которых использована информация о поведении функции в некотором конечном наборе точек, называемых узлами интерполяции и принадлежащих ее области определения. Формальная экстраполяция сводится к математически оптимальной подгонке исходного статистического ряда к какой-либо аппроксимирующей функции. Критерием оптимальности здесь может выступать близость точек ряда к аппроксимирующей функции. Прогнозная экстраполяция строится на основе математического анализа исходного ряда с учетом логики и существа развития объекта, его физики и абсолютных пределов.
Следующим этапом построения является анализ полученной модели и Выбор метода ее решения. Основой для вычисления значений выходных характеристик модели служит составленный на ее базе алгоритм решения задачи на ЭВМ. Разработка и программирование такого алгоритма, как правило, не имеет принципиальных трудностей.
Более сложной является организация вычислительного процесса для нахождения выходных характеристик, лежащих в допустимых областях, особенно для многофакторных моделей. Еще более сложным является поиск решений по оптимизационным моделям. Самая совершенная и адекватная описываемому процессу математическая модель без нахождения оптимального значения бесполезна, поскольку не может быть использована.
Основную роль при разработке алгоритма поиска оптимальных решений играет характер факторов математической модели, число критериев оптимальности, вид целевой функции и уравнение связи. Вид целевой функции и ограничений определяет выбор одного из трех основных методов решения экономико-математических моделей:
• исследования при помощи численных методов;
• исследования алгоритмических моделей с помощью методов экспериментальной оптимизации на ЭВМ.
Аналитические методы отличаются тем, что помимо точного значения искомых переменных они могут давать оптимальное решение в виде готовой формулы, куда входят характеристики внешней среды и начальные условия, которые исследователь может изменить в широких пределах, не меняя самой формулы.
Численные методы дают возможность получить решения путем многократного вычисления по определенному алгоритму, реализующему тот или иной численный метод. В качестве исходных данных для вычислений используются числовые значения параметров объекта, внешней среды и начальных условий. Численные методы являются итеративными процедурами: для проведения следующего шага расчетов (при новом значении управляемых переменных) используются результаты предыдущих расчетов, что позволяет получать в процессе вычислений улучшенные результаты и находить оптимальное решение.
Свойства конкретной алгоритмической модели, на которой базируется алгоритм поиска оптимального решения, например ее линейность или выпуклость, могут быть определены только в процессе экспериментирования с ней, в связи с чем для решения моделей этого класса используются так называемые методы экспериментальной оптимизации на ЭВМ. При использовании этих методов производится пошаговое приближение к оптимальному решению на основе результатов расчета по алгоритму, моделирующему работу исследуемой системы. Методы базируются на принципах поиска оптимальных решений в численных методах, но в отличие от них все работы по разработке алгоритма и программы оптимизации выполняет разработчик модели.
⇐ Предыдущая Стр 16 из 16
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав — Главная | Случайная страница | Контакты —>
Источник: studopedia.su
