Умения и навыки, которые должны приобрести обучаемые на занятии:
— практически изучить методы определение класса точности и системы приборов электроизмерительных приборов;
— производить расчет погрешностей по условным обозначениям на шкалах приборов и выяснить, для каких измерений можно применять эти приборы;
— рассмотреть схемы включения приборов различных систем в электрическую цепь.
Наглядные пособия, оборудование: Компьютер, проектор, измерительные приборы различных систем.
Повторение теоретических основ:
1. Классы точности электроизмерительных приборов (ИП).
2. Типы систем ИП.
3. Определение погрешностей ИП.
1. Классы точности электроизмерительных приборов
Точность измерения — качество измерения, отражающее близость его результатов к истинному значению измеряемой величины. Высокая точность измерений соответствует малой погрешности.
Погрешность измерительного прибора — разность между показаниями прибора и истинным значением измеряемой величины.
Относительная погрешность и класс точности прибора
Результат измерения — значение величины, найденное путем ее измерения.
При однократном измерении показание прибора является результатом измерения, а при многократном — результат измерения находят путем статистической обработки результатов каждого наблюдения. По точности результатов измерения подразделяют на три вида:
— очные (прецизионные), результат которых должен иметь минимальную погрешность;
— контрольно-поверочные, погрешность которых не должна превышать некоторого заданного значения;
— технические, результат которых содержит погрешность, определяемую погрешностью измерительного прибора.
Как правило, точные и контрольно-проверочные измерения требуют многократных наблюдений.
По способу выражения погрешности средств измерений разделяют на абсолютные, относительные и приведенные.
Абсолютная погрешность ΔА — разность между показанием прибора А и действительным значением измеряемой величины А.
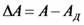
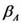
Относительная погрешность — отношение абсолютной погрешности ΔА к значению измеряемой величины А, выраженное в процентах:
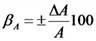
.
Приведенная погрешность 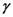 (в процентах) — отношение абсолютной погрешности ЛА к нормирующему значению
(в процентах) — отношение абсолютной погрешности ЛА к нормирующему значению 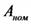 :
:
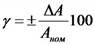
.
Для приборов с нулевой отметкой на краю или вне шкалы нормирующее значение равно конечному значению диапазона измерений. Для приборов с двухсторонней шкалой, т. е. с отметками шкалы, расположенными по обе стороны от нуля, оно равно арифметической сумме конечных значений диапазона измерений. Для приборов с логарифмической или гиперболической шкалой нормирующее значение равно длине всей шкалы.
Понятие класса и объекта в ООП
Таблица 1 — Классы точности средств измерений
| Класс точности прибора | Класс точности шунта, добавочного резистора | Класс точности измерительного преобразователя | Класс точности измерительного трансформатора |
| 1,0 1,5 2,5 | 0,5 0,5 0,5 | 0,5 0,5** 1,0 | 0,5 0,5** 1,0*** |
| *Класс точности численно равен наибольшей допустимой приведенной основной погрешности, выраженной в процентах. **Допускается 1,0. ***Допускается 3,0. |
Средства измерений электрических величин должны удовлетворять следующим основным требованиям (ПУЭ):
1) класс точности измерительных приборов должен быть не хуже 2,5;
2) классы точности измерительных шунтов, добавочных резисторов, трансформаторов и преобразователей должны быть не хуже приведенных в табл. 1.;
3) пределы измерения приборов должны выбираться с учетом возможных наибольших длительных отклонений измеряемых величин от номинальных значений.
2. Типы систем электроизмерительных приборов
По принципу действия электромеханические приборы подразделяются на приборы магнитоэлектрической, электромагнитной, ферродинамической, индукционной, электростатической систем. Условные обозначения систем приведены в табл. 2.
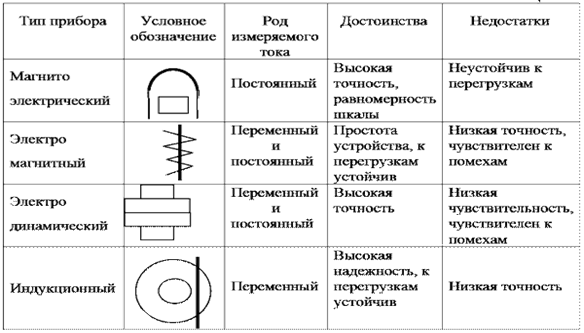
Таблица 2 -Системы электроизмерительных приборов
Примеры определения класса точности и погрешностей ИП
Задача1 Определить класс точности прибора если наибольшая абсолютная погрешность при измерении напряжения милливольтметром с верхним пределом измерения 100 мВ при измерении напряжения 20 мВ cоставляет 1,2 мВ.
Решение:
Определим приведённую погрешность прибора:
= 1,2 мV ∙ 100% / 100 мV = 1,2%.
Следовательно, такую погрешность измерения можно допустить, пользуясь прибором класса точности 1,5 и грубее.
Задача №2 Чему равна набольшая возможная разница показаний вольтметров, если при измерении напряжения двумя вольтметрами у первого класс точности – 1,0, предел измерения – 300 В, а у второго соответственно – 2,5 и 250 В.
Решение:
Наибольшая разница в показаниях приборов будет наблюдаться в случае, когда один прибор покажет результат с предельной погрешностью со знаком «+», а второй – со знаком «–». Следовательно, для решения этой задачи необходимо рассчитать предельные абсолютные погрешности приборов и сложить их по абсолютной величине.
Приведенная погрешность: , откуда ∆1 = 1% ∙ 300 В / 100% = 3В; ∆2 = 2,5% ∙ 250 В / 100% = 6,25 В.
Наибольшая разница показаний 3 + 6,25 = 9,25 В.
Задания для самостоятельного выполнения:
Задача 1 Какой класс точности должен иметь амперметр, имеющий предел измерения 10 А, при измерении тока 7 А с погрешностью не более 1,2%?
Задача 2 Проведены 11 равноточных измерений напряжения. Результаты следующие: 130,2; 130,3; 130,2; 130,3; 130,2; 129,6; 129,8; 129,9; 130,1; 129,9; 129,3 В. Результаты измерений распределены нормально, дисперсия не известна. Оценить доверительный интервал истинного значения для вероятности 0,95(tР = 2,228).
Задача 3 Какой результат округления примет вид после обработки многократных измерений напряжения U = 170,457 В и ∆ = 0,814 В?
Задача 1 Сколько составляет допустимая относительная погрешность измерения тока 7,5 А амперметром класса точности 1,5 с верхним пределом измерения 10 А?
Задача 2 Определите класс точности амперметра если при поверке амперметра с пределом измерения 5 А в точках 1, 2, 3, 4, 5 А получили соответственно следующие показания образцового прибора: 0,95; 2,07; 3,05; 4,08; 4,95.
Задача 3 В наличии имеются четыре вольтметра. Первый вольтметр класса точности 0,5 с пределом измерения 250 В; второй – класса точности 1,0 с пределом измерения 1000 В; третий – класса точности 4,0 с пределом измерения 300 В; четвертый – класса точности 0,8/0,6 с поддиапазонами измерения 50, 500, 1000 В. Какие вольтметры (WV1, WV2, WV3, WV4) подойдут lля измерения напряжения 200 В с погрешностью не более 2%?
Контрольные вопросы:
1. Что значит измерить электрическую величину?
2. Что называется измерительным прибором?
3. Что такое абсолютная погрешность прибора?
4. Что такое класс точности прибора?
5. Какие условные обозначения наносят на шкалу?
6. Что такое чувствительность и предел измерения прибора?
7. Как включается в цепь амперметр и вольтметр?
8. Почему амперметр должен иметь малое внутреннее сопротивление?
9. Почему вольтметр должен иметь большое сопротивление?
10. Можно ли при измерениях амперметр включать в цепь параллельно?
11. Можно ли при измерениях включать вольтметр в цепь последовательно?
Источник: poisk-ru.ru
Как определить класс точности прибора
Класс точности является одной из основных характеристик любого измерительного прибора. Для каждого класса существует определенный размер допустимой погрешности. Любые измерения проводятся для того, чтобы получить наиболее достоверные данные о физических данных объекта. Измерительный прибор должен соответствовать поставленной задаче. При оценке его качества необходимо учесть несколько параметров, в том числе и класс точности.

Статьи по теме:
- Как определить класс точности прибора
- Как оценить риски
- Как рассчитать рейтинг
Вам понадобится
- — прибор;
- — нормативная документация на прибор.
Инструкция
Класс точности прибора обычно указывается на шкале. Он указывается и в инструкции, которая прилагается к прибору. Посмотрите, какими символами он обозначен. Это могут быть прописные латинские буквы, римские или арабские цифры. В последнем случае добавляется какой-либо дополнительный символ.
Если класс точности обозначен латинской маркировкой, это означает, что определяется он по абсолютной погрешности. Арабские цифры без дополнительных значков свидетельствуют о том, что определяющей является приведенная погрешность, при этом учитывается максимальное или минимальное значение возможного измерения. Дополнительным значком может быть, например, галочка. В этом случае также определение класса идет по приведенной погрешности, однако на основании длины шкалы. При определении класс по относительной погрешности проставляются римские цифры.
Прибор может не иметь никакой маркировки. Это значит, что погрешность может составлять более 4%, то есть пользоваться им можно только для очень приблизительных измерений. В этом случае размер погрешности установите сами. Он приблизительно равен половине цены деления. При этом результат измерения может быть как больше истинного на размер погрешности, так и меньше.
Маркировка должна соответствовать государственным стандартам.
Вычислите погрешность. Класс точности определяется как отношение той или иной погрешности к точному значению. Например, абсолютную можно представить в виде разности между точным и приблизительным значениями х и а, то есть в виде формулы s=(x-a) Относительная определяется как отношение этой же разнице к величине а, а приведенная – к длине шкалы l. Умножьте полученный результат на 100%.
Существует восемь классов точности стрелочных приборов. Они определяются по приведенной погрешности. Делятся они на прецизионные и технические. Первые применяются для точных измерений – например, в лабораториях. Диапазон погрешностей у этих классов – от 0,05 до 0,5.Приборы, относящиеся ко второй категории, Они могут давать погрешность от 1,0 до 4, 0. При этом по всей длине шкалы расхождение между данными измерения и фактическим значением одно и то же.
Источник: www.kakprosto.ru
Погрешности средств измерений. Класс точности прибора

В результате воздействия большого числа факторов, влияющих на изготовление и эксплуатацию средств измерений, показания приборов отличаются от истинных значений измеряемых ими величин. Эти отклонения характеризуют погрешность средств измерений. Погрешности СИ в отличие от погрешности измерений имеют другую физическую природу, так как они от носятся к СИ, с помощью которого осуществляют измерение. Они являются лишь составной частью погрешности измерения.
Классификация погрешностей средств измерений в зависимости от разных признаков:
| Погрешности измерительных средств | ||||
| От характера проявления | От условий применения | От режима применения | От формы представления | От значения измеряемой величины |
| — систематическая -случайная | — основная — дополнительная | — статическая — динамическая | — абсолютная -относительная -приведенная | — аддитивная — мультипликативная — линейности -гистерезиса |
В понятия абсолютной, относительной, систематической и случайной погрешностей вкладывается тот же смысл, что и в понятия погрешностей измерений.
Приведенная погрешность средства измерений равна отношению абсолютной погрешности прибора ΔХ к некоторому нормирующему значению XN :
γ = ΔX/XN или γ = 100% ΔХ/XN .
Таким образом, приведенная погрешность является разновидностью относительной погрешности прибора. В качестве нормирующего значения XN принимают диапазон измерений, верхний предел измерений, длину шкалы и др.
Основная погрешность — погрешность средства измерений, используемого в нормальных условиях. При эксплуатации СИ на производстве возникают значительные отклонения от нормальных условий, вызывающие дополнительные погрешности.
Нормальными условиями для линейных измерений считаются:
• температура окружающей среды 20°С
• атмосферное давление 101325 Па (760 мм рт.ст.)
• относительная влажность окружающего воздуха 58%
• ускорение свободного падения 9,8 м/с
• направление линии и плоскости измерения — горизонтальное
• относительная скорость движения внешней воздушной среды равна нулю.
В тех случаях, когда средство измерения применяется для измерения постоянной или переменной во времени величины, для его характеристики используют понятия статическая и динамическая погрешности соответственно. Динамическая погрешность определяется как разность между погрешностью измерения в динамическом режиме и его статической погрешностью, равной значению величины в данный момент времени. Динамические погрешности возникают вследствие инерционных свойств средств измерения.
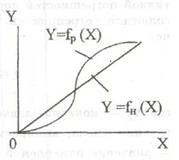
Для рассмотрения зависимости погрешности средства измерения от значения измеряемой величины используют понятие номинальной и реальной функций преобразования — соответственно Y = fн(Х) и Y = fр(X).
Номинальная функция преобразования приписана измерительному устройству, указывается в его паспорте и используется при выполнении измерений.
Реальной функцией преобразования называют ту, которой обладает конкретный экземпляр СИ данного типа.
Реальная функция преобразования имеет отклонение от номинальной функции и связана со значением измеряемой величины. Систематическую погрешность в функции измеряемой величины можно представить в виде суммы погрешности схемы, определяемо самой структурной схемой средства измерений, и технологических погрешностей, обусловленных погрешностями изготовления его элементов. Технологические погрешности принято разделять на аддитивную, мультипликативную, гистерезиса и линейности.
Аддитивной погрешностью (получаемой путем сложения), или погрешностью нуля, называют погрешность, которая остается постоянной при всех значениях измеряемой величины.
Мультипликативная погрешность (получаемая путем умножения), или погрешность чувствительности СИ, линейно возрастает или убывает с изменением измеряемой величины. В большинстве случаев аддитивная и мультипликативная составляющие присутствуют одновременно.
Погрешность гистерезиса, или Погрешность обратного хода, выражается в несовпадении реальной функции преобразования при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины. Если взаимное расположение номинальной и реальной функций преобразования средства измерений вызвано нелинейностью, то эту погрешность называют погрешностью линейности.
 | 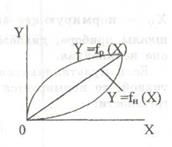 |  |
| Аддитивная и мультипликативная погрешности | Погрешность гистерезиса | Погрешность линейности |
В разных точках диапазона средств измерений погрешность может принимать различные значения. В этом случае необходимо нормировать пределы допускаемых погрешностей, т.е. устанавливать границы, за пределы которых погрешность не должна выходить ни при изготовлении, ни в процессе эксплуатации. Для этого служит класс точности СИ.
Класс точности — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды средств измерений.
Способы установления классов точности изложены в ГОСТ 8.401 “ГСИ. Классы точности средств измерения. Общие требования”. Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие величины. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность.
Класс точности не является непосредственным показателем точности измерений, так как точность измерений зависит еще от метода и условий измерений.
В зависимости от вида погрешности средства измерений существует несколько способов нормирования погрешности.
Если аддитивная погрешность СИ преобладает над мультипликативной, удобнее нормировать абсолютную или приведенную погрешности соответственно:
Нормирование по абсолютной погрешности не позволяет сравнивать по точности приборы с разными диапазонами измерений, поэтому принято нормировать приведенную погрешность, где р — отвлеченное положительное число, выбираемое из ряда
(1,5; 2; 2,5; 4; 5; 6) 10* (п = 1, О, — 1, — 2 и т.д.);
XN — нормирующее значение, равное конечному значению шкалы прибора, диапазону измерений или длине шкалы, если она нелинейная.
Если мультипликативная погрешность преобладает над аддитивной, то нормируется предел допускаемой относительной погрешности:
где q — отвлеченное положительное число, выбираемое из ряда, приведенного для р.
При одновременном проявлении аддитивной и мультипликативной погрешностей нормируется предел относительной или абсолютной погрешностей, определяемых формулами соответственно:
где Хк — конечное значение шкалы прибора; с и d — положительные числа, выбираемые из ряда, приведенного для р; Xизм — значение измеряемой величины на входе(выходе) средств измерений или число делений, отсчитанных по шкале; а и b положительные числа, не зависящие от Xизм.
Обозначение классов точности в документации и на средствах измерений приведены в табл.
Если пределы допускаемой погрешности средств измерений задаются в виде графиков, таблиц или в сложной форме, то классы точности обозначаются римскими цифрами или прописными буквами латинского алфавита.

Регулировка и градуировка средств измерений
В большинстве случаев в измерительном приборе (преобразователе) можно найти или предусмотреть такие элементы, вариация параметров которых наиболее заметно сказывается на его систематической погрешности, главным образом погрешности схемы, аддитивной и мультипликативной погрешностях.
В общем случае в конструкции измерительного прибора должны быть предусмотрены два регулировочных узла: регулировка нуля и регулировка чувствительности. Регулировкой нуля уменьшают влияние аддитивной погрешности, постоянной для каждой точки шкалы, а регулировкой чувствительности уменьшают мультипликативные погрешности, меняющиеся линейно с изменением измеряемой величины. При правильной регулировке нуля и чувствительности уменьшается и влияние погрешности схемы прибора. Кроме того, некоторые приборы снабжаются устройствами для регулировки погрешности схемы (пружинные манометры).
Таким образом, под регулировкой средств измерения понимается совокупность операций, имеющих целью уменьшить основную погрешность до значений, соответствующих пределам ее допускаемых значений, путем компенсации систематической составляющей погрешности средств измерений, т.е. погрешности схемы, мультипликативной и аддитивной погрешностей.
Градуировкой называется процесс нанесения отметок на шкалы средств измерений, а также определение значений измеряемой величины, соответствующих уже нанесенным отметкам, для составления градуировочных кривых или таблиц.
Различают следующие способы градуировки:
— использование типовых (печатных) шкал, которые изготовляются заранее в соответствии с уравнением статической характеристики идеального прибора;
— индивидуальная градуировка шкал. Индивидуальную градуировку шкал осуществляют в тех случаях, когда статическая характеристика прибора нелинейна или близка к линейной, но характер изменения систематической погрешности в диапазоне измерения случайным образом меняется от прибора к прибору данного типа так, что регулировка не позволяет уменьшить основную погрешность до пределов ее допускаемых значений.
Индивидуальную градуировку проводят в следующем порядке. На предварительно отрегулированном приборе устанавливают циферблат с еще не нанесенными отметками. К измерительному прибору подводят последовательно измеряемые величины нескольких наперед заданных или выбранных значений. На циферблате нанося отметки, соответствующие положениям указателя при этих значениях измеряемо величины, а расстояния между отметками делят на равные части. При индивидуальной градуировке систематическая погрешность уменьшается во всем диапазоне измерения, а в точках, полученных при градуировке, она достигает значения, равного погрешности обратного хода;
— градуировка условной шкалы. Условной называется шкала, снабженная некоторыми условными равномерно нанесенными делениями, например, через миллиметр или угловой градус. Градуировка шкалы состоит в определении при помощи образцовых мер или измерительных приборов значений измеряемой величины соответствующих некоторым отметкам, нанесенным на ней.
В результате определяют зависимость числа делений шкалы, пройденных указателем, от значений измеряемой величины. Эту зависимость представляют в виде таблицы или графика. Если необходимо избавиться и от погрешности обратного хода. Градуировку осуществляют раздельно при прямом и обратном ходе.
Источник: megaobuchalka.ru
