1) 49 : 21 = 2.33
2) 4500 : 2000 = 2.5
Вывод — номера «ЛЮКС» — приносят БОЛЬШЕ дохода
Делим разрешенные 1099 кв.м в отношении 2,5 : 2,33 = 1,073
И получаем
1099 : 2,073 = 530 — для «бюджетных»
Делим на отдельные номера по 21 кв.м и выделяем на них
530 : 21 = 25.2 ~ 26 номеров или
26*21 = 546 кв.м — бюджетных
и 1099 — 546 = 553 кв.м — под «люкс»
Или в целых номерах и
553 : 49 = 11,2 ~ 11 номеров «люкс»
И расчет дохода
2000 * 26 + 4500*11 = 52000 + 49500 = 101 500 руб — ОТВЕТ
0,0(0 оценок)
Источник: znaniija.ru
Презентация на тему Решение экономических задач. Задача №17 ЕГЭ
Слайд 1
Решение экономических задач.
Задача №17 егэ-2016

Предприниматель купил здание и собирается открыть в нем отель Задача на оптимизацию. ЕГЭ профиль
Слайд 2 В двух шахтах добывают алюминий
и никель. В первой шахте имеется 100 рабочих, каждый из
которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Слайд 3
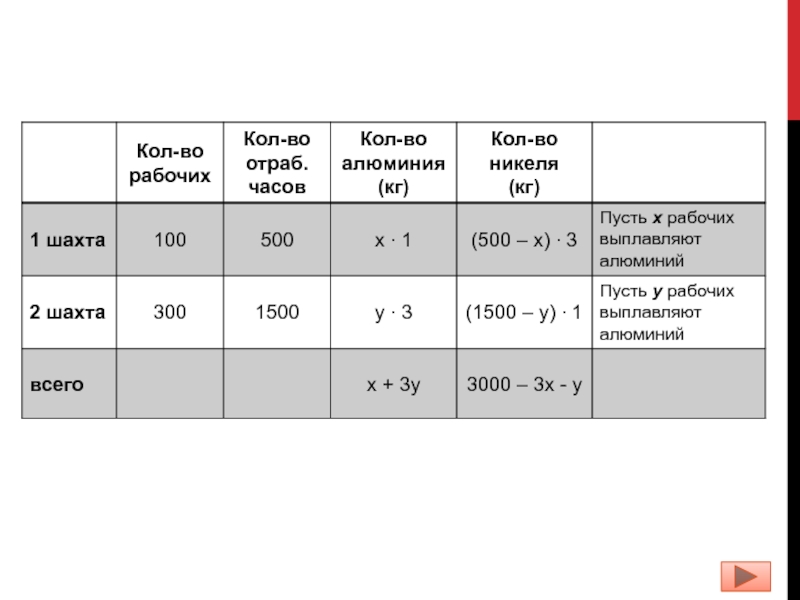
Слайд 4

Слайд 5 Предприниматель купил здание и собирается открыть
в нем отель. В отеле могут быть стандартные номера площадью
21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Предприниматель купил здание и собирается открыть в нем отель.
Слайд 6

Слайд 7 В двух областях есть по 50 рабочих, каждый
из которых готов трудиться по 10 часов в сутки на
добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля. При этом области договариваются между собой вести добычу металла так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Слайд 8В первой области 50 рабочих отработают 500 часов в сутки.
Пусть z человек выпускают алюминий. Количество металла выпущенное в первой
области z ∙ 0,2 + (500 – z) ∙ 0,1 кг. А во второй области так же 500 человеко-часов и по условию задачи х2 + у2 = 500, т.е. х2 = 100, у2 = 400; х = 10, у = 20. 10 кг алюминия и 20 кг никеля добывают во второй области. Так как никеля выпускают в 2 раза больше, то 2(0,2z + 10) = 50 – 0,1z + 20, 0,4z + 20 = 70 — 0,1z, 0,5z = 50, z = 100. S(z) = 0,2z + 50 – 0,1z + 30. S(100) = 0,2 ∙ 100 + 50 – 0,1 ∙ 100 + 30 = 20 + 50 – 10 + 30 = 70 + 20 = 90.
Ответ: 90 кг сплава за сутки.

Слайд 9 У фермера есть два поля,
каждое площадью 10 гектаров. На каждом поле можно выращивать картофель
и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором – 200ц/га. Урожайность свеклы на первом поле составляет — 200 ц/га, а на втором – 300 ц/га. Фермер может продавать картофель по цене 10 000 руб. за центнер, а свеклу — по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?

Слайд 10 Пусть х га на первом поле отводится под
свеклу, а (10 – х) га отводится под картофель.
С первого поля собирают 300(10 – х) ц картофеля и 200х ц свеклы. Пусть у га на втором поле отводится под свеклу, а (10 – у) га отводится под картофель. Со второго поля собирают 200(10 ∙ у) ц картофеля и 300 у ц свеклы Прибыль с первого поля (30 000 000 – 3 000 000х + 2 600 000х) руб., а прибыль со второго поля (20 000 000 – 2 000 000у + 3 900 000у) руб. . Функция прибыли с двух полей S(х; у) = 1 900 000у – 400 000х + 50 000 000. Наибольшее значение функции принимает при х = 0, а у = 10, тогда прибыль составит 69 000 000 руб. Ответ: 69 000 000 рублей наибольший доход фермера.

Слайд 11 Предприниматель купил здание и собирается открыть
в нем отель. В отеле могут быть стандартные номера площадью
27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Источник: theslide.ru
Задачи на нахождение количества лет выплаты кредита.
Задача 1. (Тренировочная работа 21) В июле Федор планирует взять в кредит 1,1 млн. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года Федор должен выплатить некоторую часть долга.
На какое минимальное минимальное количество лет Федор может взять кредит, чтобы ежегодные выплаты были не более 300тысяч рублей?
1) В конце первого года долг составит:
1100000∙1,1 — 300000 = 910000
2) В конце второго года долг составит:
910000∙1,1 — 300000 = 701000
3) В конце третьего года долг составит:
701000∙1,1 — 300000 = 471000
4) В конце четвертого года долг составит:
471000∙1,1 — 300000 = 218210
5) В конце пятого года долг составит:
218210∙1,1 — 300000 0, т.е. кредит будет погашен за 5 лет.
Задачи на оптимизацию.
Задача 1. (Тренировочная работа 16).У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400ц/га, а на втором — 300ц/га. Урожайность свеклы на первом поле составляет 300ц/га, а на втором — 400ц/га.
Фермер может продавать картофель по цене 5000руб. за центнер, а свеклу — по цене 6000руб. за центнер. Какой наибольший доход может получить фермер?
Решение: Посчитаем доход фермера с 1-го поля:
1) если засеет на нем картофель, урожайность — 400ц/га, 1ц = 5000рублей
с 10 га он соберет 400ц/га∙10га = 4000ц тогда доход:
4000∙5000= 20000000рб = 20млн.
2) если засеет свеклу, урожайность — 300ц/га, 1ц = 6000 рублей
с 10 га он соберет 300∙10=3000ц, тогда доход:
3000∙6000 = 18000000рублей = 18млн.
Теперь посчитаем доход фермера со 2-го поля:
1) если засеет картофель, урожайность — 300ц/га
с 10 га он соберет 300∙10 = 3000 ц, тогда доход
3000∙5000 = 15000000 рублей = 15млн
2) если засеет свеклу, урожайность свеклы — 400ц/га
с 10 га он соберет 400∙10 = 4000ц, доход будет равен:
4000∙6000 = 24000000рублей = 24млн
Отсюда видно, что максимально возможный доход:
20млн + 24млн = 44млн. Ответ: 44млн.
Задача 2 (Тренировочная работа 34). Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет.
Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег может заработать в сутки на своем отеле предприниматель?
Найдем стоимость 1м² стандартного номера = 2000_27=74 руб.
Найдем стоимость 1м² номера «люкс» =4000:45=88 =88 руб.
Так как стоимость 1м 2 номера «люкс» дороже, то выгоднее разместить на этой площади больше номеров «люкс», и как можно меньше номеров стандартных. Начнем перебор количества номеров стандартных с наименьшей цифры.
Пусть стандартных номеров будет:
— 0, тогда 981:45≠ (нацело не делится), далее
— 1, тогда 981 — 27 = 954, 954:45≠ также нацело не делится, далее
— 2,тогда 981 — 54 = 927, 927:45≠ также не делится, идем далее
— 3,тогда 981 — 81 = 900, 900_45=20 — номеров «люкс»
Тогда в сутки отель может заработать:
Задача 3. (Тренировочная работа 14) В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0.2 кг. алюминия или 0.1 кг. никеля. Во второй области для добычи х кг. алюминия в день требуется у² человеко-часов труда. Для нужд промышленности можно использовать или алюминий или никель, причем 1 кг. алюминия можно заменить 1 кг. никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?
Решение: 1). В 1 области работают 250 рабочих, каждый работает по 5ч в сутки. За один час один рабочий добывает 0,2кг алюминия, или 0,1кг никеля, т.е в сутки могут добыть:
250∙5∙0.2= 250 кг. алюминия или
250∙5∙0,1=125 кг. никеля. Отсюда видно, что выгоднее будет, если все будут добывать алюминий.
2) Во второй области также работают 250 человек, также работают по 5ч в сутки. Для добычи х кг алюминия требуется х 2 человеко-часов, а для добычи у кг никеля требуется у 2 человеко-часов, т.е 250 рабочих нужно разделить таким способом, чтобы извлекался корень
= =25 кг.(никель) = =25 кг.(алюминий)
Задача 4. (Тренировочная работа 20) В двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3кг алюминия или 0,1кг никеля.
Во второй области для добычи х кг алюминия в день требуется х 2 человеко-часов труда, а для добычи у кг никеля в день требуется у 2 человеко-часов труда. Обе области поставляют добытый метал на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: Решение начнем со второй области
100 рабочих нужно разбить так, чтобы извлекался корень, т.е
Теперь 1 область: пусть х — число рабочих добывающих алюминий,
тогда 100-х число рабочих добывающих никель.
х∙10∙0,3 = 3х — кг алюминия
(100 — х)∙10∙0,1 = 100 — х -кг никеля.
Составим уравнение учитывая, что на 2 кг алюминия приходится 1 кг никеля: 10 + 3х = 2(30+100 — х),
10 + 3х = 260 — 2х
5х = 250, х = 50 — рабочих на добычу алюминия, следовательно 50 рабочих на добычу никеля
50∙10∙0,3 = 150 кг алюминия
50∙10∙0,1 = 50 кг никеля.
Тогда 150 + 50 + 10 + 30 = 240кг
Задача 5. (Тренировочная работа 47). В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день.
При этом один рабочий за час добывает 3кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: Так как в 1-й шахте добывают больше никеля, то для наибольшей выгоды нужно, чтобы все рабочие добывали никель. Тогда
100∙5∙3 = 1500кг никеля будет добыто в 1-й шахте.
Пусть все 300 рабочих второй вахты добывают алюминий, тогда
300∙5∙3 = 4500кг алюминия будет добыто.
Так как для сплава нужно 2 раза больше алюминия, то рабочих второй шахты нужно распределить на добычу алюминия и никеля с учетом пропорции сплава.
Пусть х — число рабочих добывающих алюминий,
300 — х — число рабочих добывающих никель.
х∙5∙3 = 15х (кг) — алюминий
(300 — х)∙5∙1 = 1500 — 5х (кг) — никель
Составляем уравнение: 15х = 2(1500 — 5х + 1500)
25х = 6000, х = 240 — количество рабочих добывающих алюминий, следовательно 60 рабочих добывают никель.
240∙5∙3 = 3600кг — алюминий
60∙5∙1 = 300кг — никель
Тогда 3600 + 300 + 1500 = 5400 кг. Ответ: 5400кг.
Задача 6. (ЕГЭ — 2017. Резервный день 28.06.2017г). Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?
Решение: Пусть х — единиц товара 1-го завода,
у — единиц товара 2-го завода.
Тогда, х + у = 70, → х = 70 — у
500х 2 + 200у 2 = S
500(700 — у) 2 + 200у 2 = S
700у 2 — 70000у + 2450000 = S
700у 2 — 70000у + 2450000 — квадратный трехчлен примет наименьшее значение при у = = 50
Тогда S = 700∙50 2 — 70000∙50 + 2450000 = 700000
Задача 7. (ЕГЭ — 2017. Резервный день). Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение: пусть х — на оплату труда рабочих 1-го завода, следовательно,
900000 — х — на оплату труда рабочих 2-го завода.
— часов работы 1-го завода
— часов работы 2-го завода
Количество произведенного товара за неделю = + и нужно найти наибольшее значение этого выражения, для этого найдем производную и найдем нули.
Решаем уравнение = 0
= 0, , возводив в квадрат с двух сторон получим: 40(900000-х) = 50х, х = 400000.
= = 40 — единиц товара 1 завод
= = 50 — единиц товара 2 завод
40+50=90 единиц. Ответ: 90.
Разные задачи
Задача 1. (Тренировочная работа 13) 15 января планируется взять в кредит в банке на сумму 2,4млн рублей на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за последние 12 месяцев?
Решение: S = 2400000. По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.
; ; ; …; . — размеры долгов (остаток по кредиту на конец месяца), тогда ежемесячная выплата процентов выглядит следующим образом:
Находим размеры выплат:
3-й месяц: + ∙ = и.т.д. Замечаем, что выходит последовательность, которая уменьшается на 2. Тогда используя формулу n-го члена арифметической прогрессии аn = а1 + d(n — 1) при а1=148, d= -2
находим 13-й месяц: а13 = 148 — 2(13 — 1) = 126, т.е. и
24-й месяц: а24 = 148 — 2(24 — 1) = 102S, т.е.
Выплата за последние 12 месяцев: +. +
Вынесем за скобки общий множитель и воспользуемся формулой суммы членов арифметической прогрессии Sn = ∙n
Задача 2. (Тренировочная работа 12). В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%.
В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?
Решение: Продать ценную бумагу нужно в тот момент, когда 10% от стоимости станут составлять не меньше 3000 рублей, что возможно при стоимости бумаги не менее 30000 рублей. это произойдет через (19+3+3+3+3=31) четыре года. И в этот момент 10% от стоимости этой бумаги будут равны 3100 рублей, т.е. больше чем, 3000 рублей. Т.е. надо продать бумагу и положить счет в банке. 2001 + 4 = 2005.
Ответ: 2005 году
2 способ решения: аn =а1+(n-1)d, а=19000
Ему будет выгодно отдать деньги в банк в том случае, если 10% от аn превышает d, т.е:
n=5 т.е бумагу можно продать в течении пятого года(сразу после 4-х лет)
Задача 3. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целоечисло миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн. рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 20 млн. рублей.
Пусть первоначальный вклад составляет S млн. руб., тогда:
В конце первого года на вкладе будет 1,1 S млн. руб.,
В конце второго года на вкладе будет 1,1 S∙1,1=1,21 S млн.руб.,
В конце третьего года на вкладе будет (1,21 S+3)∙1,1=1,331 S+3,3 млн. руб.,
В конце четвертого года на вкладе будет (1,331 S+3,3+3)∙1,1=1,4641S+6,93 млн. руб.,
Далее необходимо решить неравенство:
S = 9 млн.руб. так как по условию S — целоечисло.
В конце первого года на вкладе будет 1,1∙9 = 9,9млн. руб.,
В конце второго года на вкладе будет 9,9∙1,1 = 10,89 млн. руб.,
В конце третьего года на вкладе будет (10,89+3)∙1,1 = 15,279 млн. руб.,
В конце четвертого года на вкладе будет (15,279+3)∙1,1 = 20,1069 млн. руб.
Задача 4. (Вариант 19. Лаппо Л.Д. ЕГЭ 2018) В мае 2017 года планируется взять кредит в банке на 6 лет в размере S млн. рублей. Условия его возврата таковы:
— каждый декабрь каждого года долг возрастает на 10%;
— с января по апрель каждого года необходимо выплатить часть долга;
— в мае 2018, 2019 и 2020 годов долг остается равным S млн. рублей;
— выплаты в 2021, 2022 и 2023 годах равны между собой;
— к маю 2023 года долг будет выплачен полностью.
Найдите наибольшее целое S, при котором общая сумма выплат не превысит 13млн. рублей.
Решение: Сумма выплат за первые три года: 0,1S∙3 = 0,3S
Сумма выплат за последние три года: 3∙х = 3х
По условию сумма выплат не превысит 13 млн: 0,3S + 3х ≤ 13 (1)
За последние три года долг станет равным нулю, т.е.
Sp 3 — p 2 x — px — x = 0, p=1,1
S∙1,1 3 — 1,1 2 x — 1,1x — x = 0
1,331S — 1,21x — 1,1x — x = 0
x = Полученное выражение подставим в (1)
S(0,3 + ) ≤ 13, S ≤ 8,63 Ответ: 8 млн.
Источник: poisk-ru.ru
