При принятии решений на уровне предприятия, в том числе малого, весьма полезны соответствующие экономико-математические и эконометрические модели. Рассмотрим несколько примеров.
Модель функционирования промышленного предприятия. Рассмотрим модель предприятия, являющегося частью более крупной экономической структуры (системы) — государственного сектора экономики, финансово-промышленной группы, транснациональной корпорации, холдинга и т.п. Предприятие действует в плановом сегменте экономики, план определяется вышестоящими органами управления. Основное внимание в модели предприятия уделяется влиянию фондов экономического стимулирования (ФРП — фонд развития производства, ФМП — фонд материального поощрения) на темпы роста прибыли.
Эти фонды (ФРП и ФМП) наполняются из прибыли, которую получило предприятие. Основная часть этой прибыли идет в бюджет вышестоящей структуры, оставшаяся — в фонды. Сверху вводятся нормативы распределения прибыли, т.е. доли от прибыли, которые идут в фонды.
Описание математической БИЗНЕС-МОДЕЛИ компании
Важно найти оптимальные величины этих нормативов, так как если нормативы будут малы, то фонды практически перестанут зависеть от темпа роста прибыли и рентабельности, как следствие, их воздействие на деятельность предприятия окажется минимальным. Фактически тут можно говорить о чрезмерно больших изъятиях средств вышестоящей структурой. С другой стороны, если в фонды идет слишком большая часть прибыли, это может привести к дефициту бюджета вышестоящей структуры.
Размер ФРП есть:
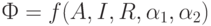
где A- стоимость основных производственных фондов;
 — отношение
— отношение 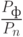 (здесь
(здесь 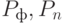 — фактический и плановый объемы реализованной продукции);
— фактический и плановый объемы реализованной продукции);

— рентабельность;
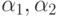
— отраслевые нормативы отчисления части прибыли в ФРП и ФМП соответственно.
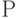
Предположим, что вышестоящей структурой выделяются капитальные вложения в количестве, прямо пропорциональном объему произведенной продукции . Пусть:

Это уравнение означает, что полный прирост капитальных вложений в основные производственные фонды равен той доле, которая выделяется на это из ФРП (  ) плюс вложения вышестоящей экономической структуры (
) плюс вложения вышестоящей экономической структуры ( 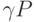 ). Коэффициент
). Коэффициент  определяется вышестоящим управляющим органом; величина
определяется вышестоящим управляющим органом; величина  зависит от величины ФРП, т.е. в конечном итоге от принятых в системе нормативов.
зависит от величины ФРП, т.е. в конечном итоге от принятых в системе нормативов.
Бизнес это математические модели
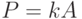
Примем, что производственная функция пропорциональна стоимости основных фондов, т.е. . Тогда

 описывает рост стоимости основных фондов. При этом пропорционально растет и объем произведенной продукции P.
описывает рост стоимости основных фондов. При этом пропорционально растет и объем произведенной продукции P.
Необходимо иметь современные научно-экономические инструменты анализа такого сравнительно нового для нашей страны вида хозяйственных объединений, как холдинги. Ясно, что без предварительного научного анализа невозможно выработать обоснованные рекомендации по повышению эффективности оперативного финансового управления компаниями холдингового типа.
В частности, в диссертации [13.1] разработана классификация компаний холдингового типа, определены основные критерии эффективности деятельности таких компаний, сформулированы принципы трансфертного ценообразования внутри холдинга. О практической направленности работы говорит внимание к разработке документооборота и сетевого графика процесса бюджетирования.
Разработаны практические рекомендации по снижению налоговых потерь. Результаты работы внедрены в холдинге, состоящем из ярославских строительных организаций. Большое значение имеет эффективная работа службы контроллинга в компании холдингового типа. При рассмотрении процесса согласования интересов хозяйствующих субъектов целесообразно использовать подходы теории кооперативных игр.
Малые предприятия. Малое предпринимательство — важная составная часть современной российской экономики. Например, в Москве более 10% населения трудится на малых предприятиях. Поэтому весьма актуальным является изучение сферы малого бизнеса с позиций экономической теории, в частности, методами экономико-математического моделирования .
Развитие малого предпринимательства необходимо для эффективного функционирования экономики России. Для понимания особенностей этого развития и управления им могут оказаться полезными разнообразные экономико-математические модели. Подходам к построению и изучению некоторых из них посвящен настоящий раздел. Дадим широкую панораму возможных подходов к построению моделей, которые могут оказаться полезными для описания динамики развития малых предприятий, а также и управления ими.
Проблемы маркетинга малого бизнеса. Во всех странах с развитой рыночной экономикой нестабильность малого бизнеса во многом связана с его сильной зависимостью от внешней среды — как от СТЭЭП-факторов (социальных, технологических, экологических, экономических, политических), так и от факторов конкурентного окружения (в т.ч. — от поставщиков и потребителей). Для того, чтобы выжить и занять свою рыночную нишу, малый бизнес должен хорошо ориентироваться и адаптироваться в условиях достаточно высокой степени неопределенности и риска. Это означает, что маркетинг малого бизнеса изначально носит рисковый характер .
Для снижения степени риска маркетинга малого бизнеса требуется высокий профессионализм менеджмента малой организации в области управления рыночной информацией и быстрота реакции в принятии решений при изменении условий внешней среды. То есть как лицо, принимающее решения ( ЛПР ), менеджер малой организации должен быть одновременно хорошим маркетологом.
Маркетинг малого бизнеса имеет особенности. Для того, чтобы малая организация могла выжить и занять свою рыночную нишу, ее маркетинг с самого начала должен быть ориентирован не на абстрактные производство и сбыт, а на конкретного потребителя с его индивидуальными запросами. Иными словами, приоритетной формой маркетинга малого бизнеса является целевой специализированный маркетинг. Он позволяет сконцентрировать объективно небольшие ресурсы малой организации на наиболее важном направлении. Однако цена ошибки ЛПР , цена принятия неправильного решения в малом бизнесе многократно возрастает, т.к. у малой организации, как правило, нет финансовых возможностей диверсифицировать свою деятельность и свой риск.
Следовательно, для менеджера малой организации наиболее важные и сложные задачи таковы: проведение маркетинговых исследований по изучению рынка, сегментация рынка, выбор целевого сегмента, оценка его потенциальной мощности, оценка риска выбора рыночной ниши и силы потенциальных конкурентов . Успешное решение перечисленных задач требует от менеджера малой организации достаточно серьезной подготовки в области теории принятия решений , эконометрики и экономико-математического моделирования, поскольку оплата услуг консалтинговых фирм по этим вопросам стоит достаточно дорого.
Вместе с тем для того, чтобы быстро реагировать на изменения внешней среды, оказывающей сильное воздействие на малую организацию, ее менеджер должен проводить постоянный мониторинг рыночной ситуации по определенным наиболее значимым параметрам (спрос, предложение, цены, товары-конкуренты, альтернативные технологии и др.). Сбор и оперативное использование такой информации является решающим фактором успеха в маркетинге малого бизнеса при принятии решений. Это требует определенных знаний и навыков у менеджера по формированию банка данных и работе с маркетинговой информацией. Наиболее доступными для менеджеров малого бизнеса являются экономико-статистические (эконометрические) методы и методы математического моделирования, позволяющие (при определенной подготовке менеджеров и наличии программной поддержки) достаточно быстро обрабатывать и использовать оперативную информацию на практике.

Математические методы и модели для решения задач малого бизнеса. Достаточно известными примерами применения методов экономико-математического моделирования в маркетинге для структурирования и анализа рыночной информации являются модели жизненного цикла товара (фирмы), модели маркетингового комплекса , матрица «Бостон-консалтинг групп», SWOT — анализ конкурентов, матрица определения проблемы и др. Они могут быть простейшими инструментами управления маркетингом в малом бизнесе и позволяют достаточно оперативно оценить место и конкурентные преимущества организаций. Вместе с тем возможности экономико-математического моделирования позволяют менеджеру самостоятельно структурировать свою собственную ситуацию и создавать собственные модели (или варианты типовых моделей с собственными значениями параметров) оптимального поведения на рынке в условиях неопределенности и риска. Так, известная среди маркетологов и менеджеров матрица «Бостон-консалтинг групп» является, на наш взгляд, не двухмерной, а трехмерной моделью, в которой наряду с долей на рынке и темпом роста продаж обязательно должен рассматриваться такой параметр , как прибыль организации.
При разработке системы экономико-математической поддержки малого бизнеса математические модели развития малого предпринимательства должны изучаться специалистами теоретически на основе вероятностных и имитационных методов и сопоставляться со статистическими данными, характеризующими реальное положение в рассматриваемой области экономики. Методология математического моделирования позволяет ставить и решать различные задачи, возникающие в маркетинге малого бизнеса. В частности, отметим задачи анализа и прогнозирования рыночной ситуации, оценки различных видов рисков.
Для повышения эффективности исследовательской работы целесообразно разделять экономико-статистические (эконометрические) методы и экономико- математическое моделирование , хотя такое деление и условно. Примером первых (т.е. методов прикладной статистики применительно к конкретным экономическим данным) являются методы выборочного изучения потребителей. Так, в 1994 г. сотрудниками Института высоких статистических технологий и эконометрики опрошены 500 потребителей и продавцов растворимого кофе, полученные результаты использованы фирмой-заказчиком при маркетинге, в частности, при планировании рекламной кампании . Технология проведения таких маркетинговых исследований близка к технологии социологических опросов, а также имеет много общего со статистическим управлением качества продукции, в частности, с оценкой качества при сертификации.
При экономико-математическом моделировании применяют нацеленные на конкретные применения модели, в отличие от моделей прикладной статистики, которые можно использовать в любой сфере деятельности. Примерами являются экономико-математические модели управления запасами (см. ниже), с помощью которых удается находить оптимальные размеры поставок и процедуру их поступления. Обычно применение таких моделей позволяет по крайней мере вдвое сократить суммарные издержки. Набор подобных компьютерных моделей должен быть рабочим инструментом менеджера малого предприятия.
При математическом моделировании маркетинговых проблем малого бизнеса используют эконометрические методы и методы экспертных оценок, а также методы имитационного моделирования. В настоящее время быстрых перемен в социальной, экономической и политической сферах отсутствуют достаточно длинные временные ряды экономических данных, и интерес исследователей и практических работников переместился из статистики временных рядов в области теории и практики экспертных оценок.
В маркетинговых исследованиях для малого бизнеса большую роль играют факторы нечисловой природы — качественные признаки, интервальные и нечеткие оценки и др. Развиваются и применяются современные методы статистического анализа нечисловых данных. Оригинальность и эффективность математического аппарата в области статистики нечисловых данных определяется тем, что он основан на использовании расстояний в выборочных пространствах, а не операций суммирования.
При изучении экономических рисков, в частности, связанных с осуществлением инвестиционных проектов, необходимо моделировать различные неопределенности будущего и настоящего. Неопределенность описывают с помощью вероятностно-статистических, нечетких, в частности, интервальных моделей. Вероятностно-статистические модели нацелены, прежде всего, на анализ массовых явлений.
Неопределенность единичных событий более целесообразно описывать с помощью нечетких множеств, в частности, с помощью интервальных чисел, задающих нижние и верхние границы для неизвестных в точности параметров. Около 30 лет назад доказано [13.20], что теория нечетких множеств в определенном смысле сводится к теории случайных множеств. Однако при практическом применении математический аппарат теории нечеткости существенно отличается от вероятностно-статистического инструментария, а также и от аппарата статистики интервальных данных.
При применении математических моделей весьма важным является исследование устойчивости выводов по отношению к допустимым отклонениям исходных данных и предпосылок модели. Только та модель может быть рекомендована для практического использования, для которой полученные с ее помощью выводы мало меняются при подобных отклонениях. Накоплен определенный опыт применения методологии экономико-математического моделирования при решении практических задач маркетинга малого бизнеса, в частности, в области товаров народного потребления и производственного назначения, образовательных услуг, а также при анализе и моделировании инфляционных процессов, в сфере налогообложения и др.
Перейдем к более подробному рассмотрению некоторых экономико-математических моделей, предназначенных для описания маркетинговой деятельности и жизненного цикла предприятий малого бизнеса.
Источник: intuit.ru
РазделIiЭкономико-математические модели планирования и анализа производственно-хозяйственной деятельности предприятия.
В современных условиях выбор оптимальных вариантов планирования и управления производством представляет серьезную проблему. В рыночных условиях проявляется жесткая конкуренция товаропроизводителей внутри страны, а также усиливаются потоки товаров, услуг и капиталов из зарубежных стран.
Поэтому нельзя принять обоснованные решения без переработки большого количества информации, характеризующей эффективность использования трудовых, материальных и денежных ресурсов. Такая задача может быть решена только с использованием ЭВМ и соответствующих экономико-математических моделей и методов. На уровне промышленных предприятий накоплен немалый опыт решения экономических задач, результаты которых успешно используются в целях планирования и управления. К ним относятся модели формирования производственной программы предприятия, оптимального использования производственных мощностей, оптимизации технологической подготовки производства (модели раскроя промышленных материалов, составления смесей) и др. В настоящее время мощности современных доступных ЭВМ и стандартное программное обеспечение позволяют реализовать эти модели на любом предприятии, фирме.
2.1 Экономико-математические модели составления производственной программы предприятия.
Рассмотрим методологические и методические вопросы составления портфеля заказов предприятия в применении к простым по экономическому содержанию моделям и методам. 2.1.1 Пример составления экономико-математической модели задачи формирования производственной программы предприятия. Постановка задачи: цех выпускает три вида изделий, производственные возможности цеха характеризуются следующими данными:
- суточный фонд времени работы оборудования 780 часов;
- суточный расход сырья 850 тонн;
- суточный расход электроэнергии 790 квт-час.
Нормы затрат производственных ресурсов на единицу различных изделий приведены в таблице 2.1: Таблица 2.1
| Ресурс | Ед. изм. | Изделия, расход ресурса на производство одного изделия | Суточный лимит (запас ресурса) | ||
| X1 | X2 | X3 | |||
| Оборудование | часы | 2 | 3 | 4 | 780 |
| Сырье | тонны | 1 | 4 | 5 | 850 |
| Электроэнергия | квт-час | 3 | 4 | 2 | 790 |
| Оптовая цена | тыс.руб | 8 | 7 | 6 | |
Составить план производства, обеспечивающий максимальный объем выпуска продукции в стоимостном выражении. Запись условия задачи в виде представленной таблицы 2.1 с объяснением данных является экономической моделью задачи. Математическая модель задачи может быть представлена в следующем виде: Пусть х1, х2 и х3 – искомые объемы выпуска 1-го, 2-го и 3-его видов изделий.
Требуется найти неотрицательные значения переменных х1, х2 и х3, обеспечивающих максимальный по стоимости выпуск продукции. 
 Совокупность выражений (2.1)÷(2.7) представляет собой математическую модель задачи.
Совокупность выражений (2.1)÷(2.7) представляет собой математическую модель задачи.
Математическая модель задачи выражений состоит из критерия оптимальности (2.1) и системы ограничений (2.2)÷(2.7). В последней можно выделить ограничение неотрицательности (2.5)÷(2.7), показывающее, какие значения могут принимать переменные., а также основные ограничения (2.2)÷(2.4), указывающие, какие преобразования можно проводить с переменными.
Система ограничений определяет множество допустимых значений переменных, из которых с помощью критерия оптимальности и отыскиваются наилучшие (по данному критерию) значения. Запишем экономико-математическую модель рассмотренной задачи в общем виде, т.е. в символах.
Введем обозначения:  индекс ресурсов (
индекс ресурсов ( = 1, 2, ….,
= 1, 2, …., );
);  индекс изделия (
индекс изделия ( = 1, 2, ….,
= 1, 2, ….,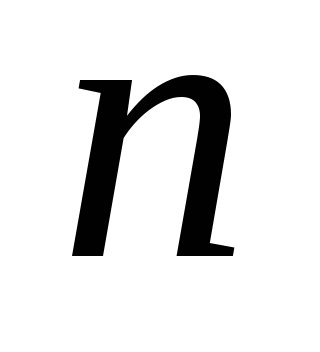 );
); 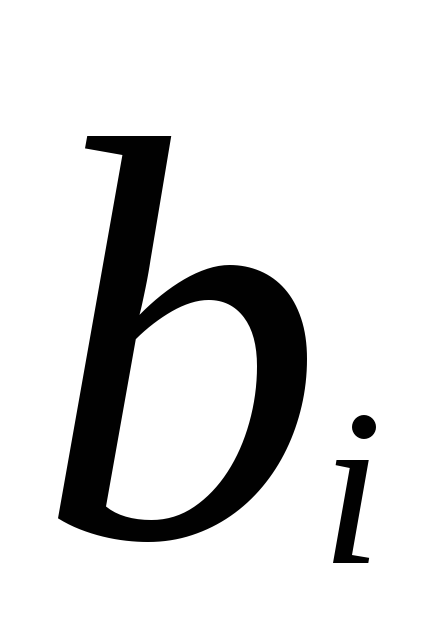 наличный объем
наличный объем  -го ресурса;
-го ресурса;  норма затрат
норма затрат  -го ресурса на производство единицы
-го ресурса на производство единицы -го изделия;
-го изделия;  оптовая цена единицы изделия
оптовая цена единицы изделия  -го вида;
-го вида;  искомый объем производства
искомый объем производства  -го изделия. В данных обозначениях задача запишется следующим образом.
-го изделия. В данных обозначениях задача запишется следующим образом.
Найти значения переменных  , максимизирующие целевую функцию вида
, максимизирующие целевую функцию вида 
 при выполнении ограничений на использование ресурсов:
при выполнении ограничений на использование ресурсов:  и неотрицательности переменных:
и неотрицательности переменных: 
 Выражение (2.8) максимизирует совокупный эффект от всего объема выпущенных изделий всех видов. Выражение (2.9) означает, что для любого из ресурсов его суммарный расход на производство изделий всех видов не превосходит всего имеющегося объема (выделенного лимита).
Выражение (2.8) максимизирует совокупный эффект от всего объема выпущенных изделий всех видов. Выражение (2.9) означает, что для любого из ресурсов его суммарный расход на производство изделий всех видов не превосходит всего имеющегося объема (выделенного лимита).
Левая часть выражения показывает используемый в оптимальном плане обьем i-го ресурса, а правая часть имеющийся обьем этого же ресурса. Выражение (2.10) означает неотрицательность выпусков изделий.
Особенность экономико-математической модели (2.8)÷(2.10) состоит в том, что она справедлива для любого количества видов продукции и ресурсов, для самых разнообразных численных значений лимитов ресурсов и норм затрат ресурсов. Коэффициенты при неизвестных в целевой функции означают эффективность от выпуска единицы продукции (прибыль, цена).
Таким образом, экономико-математическая модель (2.8)÷(2.10) соответствует любой экономической задаче по отысканию максимума эффекта от выпуска продукции при ограничениях на количество используемых ресурсов (при условии линейной зависимости эффекта и использования ресурсов от объема выпуска). Задача формирования производственной программы может быть поставлена и на минимум целевой функции.
Например, необходимо отобрать в план такие изделия, чтобы суммарные затраты на изготовление продукции были минимальными. Если принять, что  ─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:
─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:  (2.11)
(2.11)  (2.12)
(2.12)  (2.13) Для модели такого вида существует простое оптимальное решение все неизвестные равны нулю.
(2.13) Для модели такого вида существует простое оптимальное решение все неизвестные равны нулю.
Действительно, при  все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
В этой упрощенной модели не учтена цель производства получение результата в виде конечной продукции, а в процессе производства необходимо сопоставление затрат и результатов. Очевидно, необходимо ввести дополнительное ограничение, которое позволило бы не сводить к нулю затраты.
В данном случае задача должна быть поставлена следующим образом: минимизация затрат при фиксированном уровне результата. Рассмотрим экономико-математическую модель задачи на минимум затрат при фиксированных планах производства.
 (2.14)
(2.14) 
 (2.15)
(2.15)  (2.16) Но любой сверхплановый выпуск увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при
(2.16) Но любой сверхплановый выпуск увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при  , а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором
, а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором .
.
Ограничить минимум затрат снизу можно при другой постановке задачи. Пусть  цена на продукцию
цена на продукцию -го вида, а
-го вида, а план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:
план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:  (2.17)
(2.17) 
 (2.18)
(2.18)  (2.19)
(2.19)  (2.20) Постановка задачи на минимум затрат имеет смысл и в том случае, если существует несколько способов производства одноименной продукции. Например, изделия проходят обработку на токарных станках, но рабочими разной квалификации, или с использованием разных технологических способов (приспособлений). В модели
(2.20) Постановка задачи на минимум затрат имеет смысл и в том случае, если существует несколько способов производства одноименной продукции. Например, изделия проходят обработку на токарных станках, но рабочими разной квалификации, или с использованием разных технологических способов (приспособлений). В модели  (2.21)
(2.21) 
 (2.22)
(2.22)  (2.23)
(2.23)  (2.24) плановое задание по выпуску продукции
(2.24) плановое задание по выпуску продукции  осуществляется подбором разных величин
осуществляется подбором разных величин , для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
, для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
Источник: studfile.net
Математические модели бизнеса
На первых этапах развития человечества, производство было примитивным, представляло собой ремесла и земледелие. Но, промышленная революция подтолкнула людей к использованию машинных технологий, упростив и ускорив процесс производства.
Технические изменения в экономической деятельности оказали влияние на социальные изменения в обществе, спрос потребителей, принципы взаимодействия всех субъектов. В наше время предприятия является достаточно сложной организационной структурой, в которой участвует много внутренних и внешних объектов. Для более эффективного взаимодействия, руководители предприятий применяют разные инструменты для оптимизации работы.
Замечание 1
Стратегический менеджмент – один из таких инструментов. Он подразумевает формирование управленческих решений, составление планов для достижения глобальных целей. Также этот инструмент нужен для того, чтобы поддерживать конкурентоспособность на рынке.
При формировании стратегии для предприятия нужно придерживаться нескольких этапов:
- Выбор направленности работы компании;
- Выбор отрасли;
- Создание тактических задач;
- Выбор стратегии и ее утверждение;
- Реализации задуманного;
- Установление обратной связи.
Для стратегического менеджмента важна системность, комплексный подход, соблюдение выбранного направления для достижения результата. При углублённом анализе всех факторов можно рассчитать все риски и скорректировать стратегию. Обратная связь нужна для того, чтобы вовремя вносить изменения в работу предприятия.

Не нашли то, что искали?
Попробуйте обратиться за помощью к преподавателям
Тип работы
Узнать стоимость
это быстро и бесплатно
Экономическое и математическое моделирование
В экономике чаще всего используют такие методы, как:
- Сравнение (для сравнения отдельных элементов или результатов работы);
- Абстракция (для анализа поведения объекта или отдельных элементов вне системы);
- Индукция и дедукция (для рассмотрения частных и общих характеристик);
- Системный подход (для анализа объектов);
- Моделирование (для наглядности).
Часто применяют математические модели, которые состоят из разных формул и выражений, описывающих явление или объект. Экономическо-математическая модель имеет ту же основу, но направлена на решение хозяйственных задач. При создании моделей экономических процессов, проще проанализировать ситуацию и подобрать оптимальные управленческие решения.
Главная особенность экономико-математических моделей – это научная обоснованность. Благодаря им можно узнать нужные параметры и количественные данные. Теоретическая часть обосновывает научность исследования, а практическая – приближает модель к реальным показателям.
Замечание 2
При создании экономическо-математических моделей нужно придерживаться определенных этапов. Нужно указать цел исследования, определить свойства модели и факторы, определить основные параметры и возможные решения, определить неявные факторы. В конце нужно вывести функцию зависимости параметров друг от друга.
Математические модели в бизнесе
На базе стратегического планирования строятся бизнес-модели для предприятия. При подробном описании каждого события в рамках компании, можно увеличить эффективность, уменьшить расходы, сформировать полное взаимодействие всех подразделений. Чаще всего используются такие модели:
- Статистические приемы для выбора управленческих решений. Для принятия решений собирается информация об одинаковых событиях, проводится их анализ и определяется сценарий, который повторяется чаще всего;
- Теория вероятности. Благодаря этому приему можно рассчитать вероятность того или иного результата;
- Статистического-вероятностные модели. Эта модель применяется чаще остальных. В процессе работы, собираются и анализируются статические данные, на основе которых рассчитывается вероятность наступления того ил иного события.

Сложно разобраться самому?
Попробуйте обратиться за помощью к преподавателям
Источник: spravochnikvs.com
