Рассмотрим множество, состоящее из n различных элементов. Требуется выбрать из них какие-нибудь k элементов и расположить эти k элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из n элементов по k элементов (упорядоченные – следовательно, последовательности и — различные размещения).
Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество
Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество
Помощь с решением задач
Любое подмножество (неупорядоченное), состоящее из k элементов, называется сочетанием из n элементов по k элементов.
Различные сочетания отличаются друг от друга только самими входящими в них элементами, порядок их следования безразличен, т.е. по условию задачи подмножества и не различны (соединены).
Число сочетаний без повторений
Число сочетаний с повторениями
Количество способов переставить элементов в заданном множестве (количество перестановок) вычисляется по формуле
Самый БОЛЬШОЙ ОФИС для ОФИСОВ за $5 МЛН на 6,000 м2 – Деньги на Коммерческой Недвижимости @ALKANOV1
При решении простейших комбинаторных задач можно использовать следующую таблицу, определяющую число множеств, состоящих из k элементов, отбираемых из множества, содержащего n элементов
| Выбор | Неупорядоченный | Упорядоченный |
| Без повтора | ||
| С повтором |
Рассмотрим разницу между сочетаниями, размещениями с повторениями, без повторений на следующих примерах.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.1 В коробке 6 шаров, пронумерованных от 1 до 6. Из коробки вынимаются друг за другом 3 шара и в этом же порядке записывают полученные цифры. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества и – различные. Повторов в подмножестве быть не может, так как шары не возвращаются в коробку.
ПРИМЕР 13.2.2. В коробке 6 шаров пронумерованных от 1 до 6. Из коробки вынимаются 3 шара и записывают число в порядке возрастания цифр. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества и дают число 123, т.е. не являются различными.
ПРИМЕР 13.2.3. Условие задачи 2.1 (шары возвращаются в коробку)
ПРИМЕР 13.2.4. Условие задачи 2.2 (шары возвращаются в коробку)
ПРИМЕР 13.2.5. Сколько различных перестановок можно составить из букв слова «комар»?
ПРИМЕР 13.2.6. Сколько различных перестановок можно составить из букв слова «задача»?
Решение: Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть .
ПРИМЕР 13.2.7. В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?
Решение: Флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать штук.
ПРИМЕР 13.2.8. Сколькими способами можно распределить 5 учеников по 3 параллельным классам?
Решение: Составим вспомогательную таблицу
Таким образом, видно, что если для одного ученика существует 3 варианта выбора класса, то для всех 5 учеников существует способов распределения по классам.
ПРИМЕР 13.2.9. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй том не стояли рядом?
Решение: Произведем рассуждения “от обратного”. Тридцать томов на одной полке можно разместить 30! способами.
Если 1 и 2 тома должны стоять рядом, то число вариантов расстановки сокращается до , т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.
Тогда искомое число способов расстановки есть
ПРИМЕР 13.2.10. Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.
Решение: По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов — . Так как команды должны играть дважды число вариантов удваивается, т.е. .
ПРИМЕР 13.2.11. Автомобильная мастерская имеет для окраски 10 основных цветов. Сколькими способами можно окрасить автомобиль, если смешивать от 3 до 7 основных цветов?
Решение: По условию задачи отбор цветов для окраски производится без повтора и порядок отбора не важен, т.е. число вариантов зависит лишь от числа отбираемых для окраски цветов — . Поэтому общее число вариантов есть
ПРИМЕР 13.2.12. Турист прошел маршрут из пункта A в пункт B, из B в C и вернулся обратно. Сколько вариантов маршрута существует, если из пункта A в пункт B ведут 3 дороги, а из B в C — 4 и нельзя возвращаться той дорогой, по которой уже прошел?
Решение: Составим схему.
Из рисунка видно, что вариантов маршрута из А в B существует 3, и из B в C – 4, т.е. всего маршрутов .
На обратном пути вариантов маршрута из С в B существует 3 (один уже пройден), и из B в А – 2, т.е. всего возможных обратных маршрутов осталось . Тогда всего вариантов маршрута .
ПРИМЕР 13.2.13. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
Решение: Рассуждения произведем несколькими способами
I способ) Первоначально 12 учеников разбивают на 2 группы по 6 человек. Это можно сделать способами.
Затем они могут распределиться по своим рядам согласно схеме
Поэтому всего способов распределения учеников будет .
II способ) Первоначально 12 учеников запускают в класс, указывая место, где каждый должен сидеть, например “второй ряд, третье место”. Так как посадочных мест также 12, то всего вариантов распределения 12!
Варианты контрольной работы могут распределиться
“I вариант – I ряд, II вариант – II ряд”
“II вариант – I ряд, I вариант – II ряд”,
Таким образом, всего способов распределения учеников будет .
По приведенным решениям видно, что результаты решений совпадают.
ПРИМЕР 13.2.14. Сколько существует вариантов расположения шести гостей за круглым шестиместным столом?
Решение: Эта задача имеет разные решения и, соответственно разные ответы – в зависимости от того, что понимать под различным расположением гостей за столом. Поэтому исследуем возможные варианты.
Если считать, что нам важно, кто сидит на каком стуле, то это простая задача на перестановки и, следовательно, всего вариантов .
Если же важно не то, кто какой стул занял, а то, кто рядом с кем сидит, то требуется рассмотреть варианты взаимного расположения гостей. В таком случае, расположения гостей, получаемые одно из другого при повороте гостей вокруг стола, фактически являются одинаковыми (смотри рисунок).
Очевидно, что для любого расположения гостей таких одинаковых вариантов, получаемых друг из друга поворотом, — шесть. Тогда общее число вариантов уменьшается в шесть раз и их остается .
В случае же, когда нас интересует только взаимное расположение гостей, то одинаковыми можно считать и такие симметричные расположения, при которых у каждого гостя остаются те же соседи за столом, только левый и правый меняются местами (смотри рисунок).
В такой постановке вопроса общее число различных вариантов расположений гостей уменьшается вдвое и составляет 60.
Отметим, что каждое решение будет считаться правильным при соответствующей постановке задачи.
ПРИМЕР 13.2.15. Семнадцать студентов сдали экзамены по 4 предметам только на “хорошо” и “отлично”. Верно ли утверждение, что хотя бы у двух из них оценки по экзаменационным предметам совпадают?
Решение: Очевидно, что в данном случае речь идет о возможных вариантах вида
| Предмет | 1 | 2 | 3 | 4 |
| Студент 1 | 4 | 4 | 5 | 5 |
| Студент 2 | 5 | 4 | 4 | 5 |
| Студент 3 | 5 | 5 | 5 | 5 |
| … | … | … | … | … |
| Студент 17 | 4 | 4 | 5 | 4 |
Данный пример можно решить способом, изложенным в примере 13.1.8., и получить количество вариантов . Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.
По “дереву решений” видно, что 16 студентов могут сдать экзамены только на “хорошо” и “отлично” так, что их результаты будут отличаться, но если студентов 17, хотя бы одно повторение обязательно будет.
При решении задач комбинаторики используются следующие правила.
Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран nспособами, то:
Правило суммы: выбрать либо A, либо B можно m+n способами.
Правило произведения. Пара объектов (A,B) в указанном порядке может быть выбрана способами.
Примеры и задачи для самостоятельного решения
Решить комбинаторную задачу.
13.2.1.1. В группе 25 студентов. Сколькими способами можно выбрать старосту, заместителя старосты и профорга?
13.2.1.2. В группе 25 студентов. Сколькими способами можно выбрать актив группы, состоящий из старосты, заместителя старосты и профорга?
13.2.1.3. Сколькими способами можно составить список из 10 человек?
Отв.: 3628800
13.2.1.4. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?
Отв.: 126126
13.2.1.5. Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить, используя для кодировки каждой из букв: а) ровно 5 символов? б) не более пяти символов?
Отв.: а)32; б) 62
13.2.1.6. Кости для игры в домино метятся двумя цифрами. Кости симметричны, и поэтому порядок чисел не существенен. Сколько различных костей можно образовать, используя числа 0,1,2,3,4,5,6?
13.2.1.7. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти различных звуков?
Отв.: 9864000
13.2.1.8. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
13.2.1.9. В некоторых странах номера трамвайных маршрутов обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?
13.2.1.10. Команда компьютера записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное количество различных команд?
13.2.1.11. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?
Отв.: 725760
13.2.1.12. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
13.2.1.13. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?
13.2.1.14. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?
Отв.: 9000000
13.2.1.15. У одного студента есть 7 DVD дисков, а у другого – 9 дисков. Сколькими способами они могут обменять 3 диска одного на 3 диска другого?
Отв.: 105840
13.2.1.16. На вершину горы ведут 7 дорог. Сколькими способами турист может два раза подняться на гору и спуститься с нее, если по одной и той же дороге нельзя проходить дважды?
13.2.1.17. У ювелира было 9 разных драгоценных камней: сапфир, рубин, топаз и т.д. Ювелир планировал изготовить браслет для часов, однако три камня было украдено. Насколько меньше вариантов браслета он может изготовить по сравнению с первоначальными планами?
Отв.: 362160
13.2.1.18. В поезд метро на начальной станции вошли 10 пассажиров. Сколькими способами могут выйти все пассажиры на последующих 6 станциях?
Отв.: 60466176
13.2.1.19. За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать?
13.2.1.20. В классе 25 учеников. Верно ли утверждение, что, по крайней мере, у трех из них день рождения в один и тот же месяц?
13.2.1.21. На участке железной дороги расположено 25 станций с билетной кассой в каждой. Касса каждой станции продает билеты до любой другой станции, притом в обоих направлениях. Сколько различных вариантов билетов можно выдать на этом участке?
13.2.1.22. На официальном приеме 50 человек обменялись рукопожатиями. Сколько было сделано рукопожатий?
13.2.1.23. Сколько диагоналей у выпуклого двадцатиугольника?
Источник: online-matematika.ru
8 задач на логику, без которых не обходится собеседование в Google и Tesla

Пожалуй, многим из нас приходилось хотя бы однажды побывать на собеседовании. И если вместо привычных вопросов по резюме и особенностям работы соискатель слышит загадку, воспоминания точно останутся незабываемыми. А ведь именно подобная «изюминка» встречается на собеседовании таких всемирно известных корпораций, как Apple, Google, и Microsoft.
1. Загадка о двух дверях

Загадка о проблеме выбора. /Фото: tyt.by
Эту задачку можно услышать в стенах цифрового гиганта Apple. Условие звучит так:
«Шелдон Купер (персонаж популярного сериала) прошел игровой квест до последнего рубежа. Теперь перед ним — две двери, одна из которых приведет к сокровищу, а вторая — в смертельно опасный лабиринт. У каждой двери стоит стражник, оба они знают, какая из них ведет к сокровищу. Вот только лишь один из них скажет правду. Шелдон не знает, кто из них врун, а кто нет.
Прежде чем сделать выбор, можно поставить всего один вопрос и только одному стражнику.
Вопрос: Что нужно спросить Шелдону у стражника, чтобы найти путь к сокровищу?»
Ответ: Можно спросить любого, сформулировав вопрос так: «Какая дверь, по мнению другого стражника, правильная?». Если он спросит у «правдоруба», то узнает, какая дверь ведет к лабиринту, ведь врущий стражник всегда врет. Если же он спросит у лжеца, то снова узнает, какая дверь ведет к лабиринту, ведь тот соврет о двери, на которую укажет правдивый стражник.
2. Инопланетяне и шапки

Противостояние инопланетному завоеванию. /Фото: fishki.net
Еще одна загадка для соискателей вакансий в Apple. Звучит она так:
«Землю захватили инопланетяне. Они хотят уничтожить всю планету, но решили дать человечеству один шанс. Они выбрали десять самых умных людей и поместили их в абсолютно темную комнату, выстроив в ряд. На каждого надели по шляпе, шляпы всего двух цветов — белые и черные. После того, как все шляпы оказываются на головах, свет включается.
Инопланетянин спрашивает последнего человека в ряду о цвете его шляпы. Ни о чем, кроме цвета шляпы, спрашивать нельзя, как и промолчать. Если он отвечает верно, остается в живых, ошибается — погибает. Цвет шляпа посмотреть нельзя, но можно договориться об определенном принципе, по которому могут ответить все. Расположение шляп — случайное, но вам видны все шляпы впереди.
Вопрос: Что нужно отвечать, чтобы выжило как можно больше людей?»
Ответ: Первый отвечающий считает количество черных шляп перед собой, если их нечетное число, он называет «черный», если четное — «белый». Следующий, видя шляпы перед собой, может таким образом вычислить, какого цвета головной убор у него на голове (к примеру, если черных все еще нечетное количество, то очевидно, что на нем — белая), и так далее. Таким методом сохраняется 9 из 10 человек.
3. Задание с мотоциклами

Полсотни мотоциклов и бесконечная дорога впереди. /Фото: motorpage.ru
Эта задачка является частым гостем собеседований в компании Adobe:
«У вас есть пятьдесят мотоциклов полным баком, бензина в котором хватает на 100 км езды.
Вопрос: Как далеко вы сможете уехать с помощью этих пятидесяти мотоциклов (учитывая, что изначально они находятся в условно одной точке)?
Ответ: Сначала необходимо перевезти все мотоциклы на пятьдесят километров. Затем, топливо из половины мотоциклов перевивается во вторую половину. В результате мы имеем 25 мотоциклов с полным баком. Повторяйте процедуру каждый пятьдесят километров. Таким образом, можно проехать 350 км.
4. Задача о двух ведрах
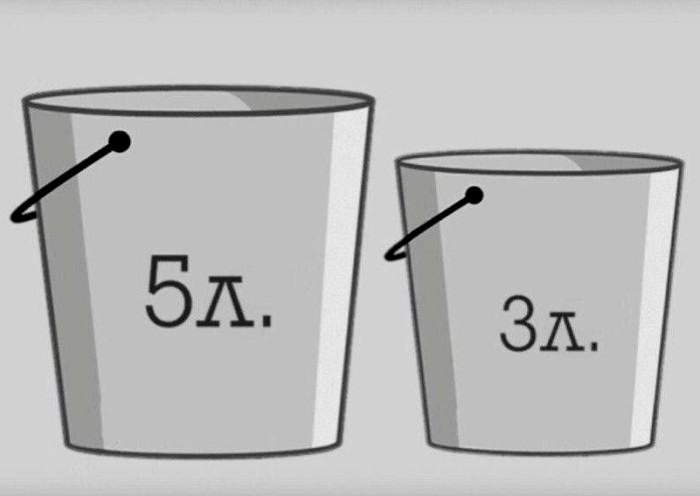
Когда нужна золотая середина, а под рукой ведра разного размера. /Фото: teletype.in
При отборе будущих сотрудников в корпорацию Microsoft используют следующую задачу:
«У вас есть бесконечный запас воды и два ведра объемом 5 литров и 3 литра соответственно.
Вопрос: Как с их помощью отмерить четыре литра?»
Ответ: Вначале наполните пятилитровое ведро и вылейте часть воды в трехлитровое. Теперь в большом ведре осталось два литра. Опустошите маленькое ведро и перелейте туда воду из большого. Снова заполните большое ведро и перелейте из него воду в меньшее. Так как в нем уже есть 2 литра, то после переливания в большом останется 4 литра.
5. Загадка о двух горящих веревках

Как с помощью веревок посчитать время. /Фото: mixstuff.ru
Необычная задачка из стен офисов Microsoft:
«У вас есть два отрезка веревки. Длина каждого из них такова, что при поджигании любого из них с одного конца он будет гореть ровно шестьдесят минут.
Вопрос: Имея только коробок спичек, как отмерить с помощью двух отрезков такой веревки 45 минут при условии, что рвать веревки нельзя?»
Ответ: Одна из веревок поджигается с двух концов, одновременно с ней поджигается вторая, но уже с одного конца. Когда первый отрезок догорит, пройдет 30 минут, от первого также останется 30-минутный отрезок. Затем поджигаем оставшуюся веревку с двух концов, и она горит еще 15 минут.
6. Задача о восьми шариках

Один размер не значит один вес. /Фото: zagadky.com
Неудивительно, что в таком информационном гиганте как Google, который способен генерировать любую информацию, есть загадки для собеседований. Условие звучит так:
«У вас имеется 8 шариков одинакового вида и размера.
Вопрос: Как найти более тяжелый шарик при условии, что использовать весы можно всего дважды?»
Ответ: Отберите шесть шариков, разделите их на группы по три шарика и поместите на весы. Те, что с более тяжелым шариком, перетянут чашу. Выберите из этой группы два любых шарика и снова взвесьте. Если тяжелый шарик среди них, вы это увидите, если они весят одинаково — тяжелым является третий шар группы. Если же более тяжелого шарика в группах по 3 шарика не оказалось, он — среди 2 оставшихся.
7. Лайфхак для собеседования от Илона Маска

Загадка-фаворит Илона Маска. /Фото: mk.ru
Оказывается, у Илона Маска есть собственная любимая загадка на случай собеседования. Условия ее таковы:
«Представьте, что вы стоите на поверхности Земли. Вы проходите одну милю на юг, одну на запад и одну на север и оказываетесь в той же точке, откуда начали движение.
Вопрос: Где вы находитесь?»
Ответ: Их два. Первый способны дать большинство инженеров — это Северный полюс. Если с Северного полюса пройти одну милю на юг, потом повернуть на запад и пройти еще одну милю, а затем сменить направление на северное, то через одну милю вы снова окажетесь на Северном полюсе, замкнув своим движением треугольник.
Второй верный ответ на загадку — вблизи Южного полюса, на одну милю севернее параллели, длина которой равна одной миле.
8. Задача-бонус

Великий учёный и сегодня поощряет активную мозговую деятельность. /Фото: facebook.com
А эту задачу мы предлагаем вас решить самостоятельно. Она интересна одной своей историей: ее предполагаемыми авторами называют не то Альберта Эйнштейна, не то Льюиса Кэрролла.
«На улице стоят пять домов.
Англичанин живет в красном доме.
У испанца есть собака.
В зеленом доме пьют кофе.
Датчанин пьет чай.
Зеленый дом стоит сразу справа от белого дома.
Тот, кто курит Old Gold, разводит улиток.
В желтом доме курят Kool.
В центральном доме пьют молоко.
Норвежец живет в первом доме.
Сосед того, кто курит Chesterfield, держит лису.
В доме по соседству с тем, в котором держат лошадь, курят Kool.
Тот, кто курит Lucky Strike, пьет апельсиновый сок.
Японец курит Parliament.
Норвежец живет рядом с синим домом.
Каждый из домов окрашен в свой цвет, в каждом доме живет представитель определенной национальности, у каждого — свой питомец, своя любимая марка сигарет и напиток.
Вопрос: Кто пьет воду? Кто держит зебру?»
Как ни крути, а и на собеседовании хотя бы первую минуту, но встречают по одежке: 5 вещей, которые просто необходимо надеть на собеседование, и 3, которые нужно «забыть» дома.
Источник: novate.ru
Решение №2638 В компании из 20 человек 15 пользуются социальной сетью «Одноклассники», а 10 – социальной сетью «ВКонтакте».
В компании из 20 человек 15 пользуются социальной сетью «Одноклассники», а 10 – социальной сетью «ВКонтакте». Выберите верные утверждения.
1) В этой компании найдётся хотя бы 5 человек, пользующихся обеими сетями.
2) Найдётся 10 человек из этой компании, которые не пользуются ни сетью «Одноклассники», ни сетью «ВКонтакте».
3) Не более 10 человек из этой компании пользуются обеими сетями.
4) В этой компании не найдётся ни одного человека, пользующегося только сетью «Одноклассники».
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Источник: Ященко ЕГЭ 2022 (30 вар).
Решение:
1) Верно , 15 пользуются «Одноклассники», 10 пользуются «ВКонтакте»: 15 + 10 = 25, а всего в компании 20 человек, значит минимум 25 – 20 = 5 человек пользуются обеими сетями.
2) Не верно , сетью «Одноклассники» пользуются 15 человек, значит тех кто не пользуется сетями максимум может быть 20 – 15 = 5.
3) Верно , наибольшее общее количество человек пользующихся каждой сетью по 10.
4) Не верно , из пункта 1) знаем, что как минимум 5 пользуются обеими сетями.
Ответ: 13.
Источник: ege314.ru
