15 января был выдан полугодовой кредит на развитие бизнеса в таблице представлен

1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?

Ответ: 4.

Комментарий.

Ответ верен. Более того «…построена математическая модель, решение сведено к исследованию этой модели…», см. критерии; в данном случае – арифметическая, числовая модель. Однако, эта модель построена неверно, т.е. она не соответствует условию. По решению видно, что сначала идет платёж долга, потом – начисление процента, а в условии – наоборот.

Оценка эксперта: 0 баллов.

Пример 2.

1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?

Ответ: 4.

Комментарий.

Здесь и ответ верен, и движение денег в целом описано верно. К сожалению, в вычислениях есть просчет в первой клетке третьей строки. Добавлен не 1%, а 10%. Эта ошибка «играет» в пользу писавшего, но вычислительная ошибка имеется.

Работает критерий на 2 балла, если в «недостаточно обосновано» включить и случай обоснования с вычислительной ошибкой.

Оценка эксперта: 2 балла.

Пример 3.

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Ответ: 22,5.

Комментарий.

Почти правильное решение. Есть один обидный (по невнимательности?) прокол: перед выплатой в июле оставшаяся половина долга также увеличивается на 5%

Оценка эксперта: 2 балла.

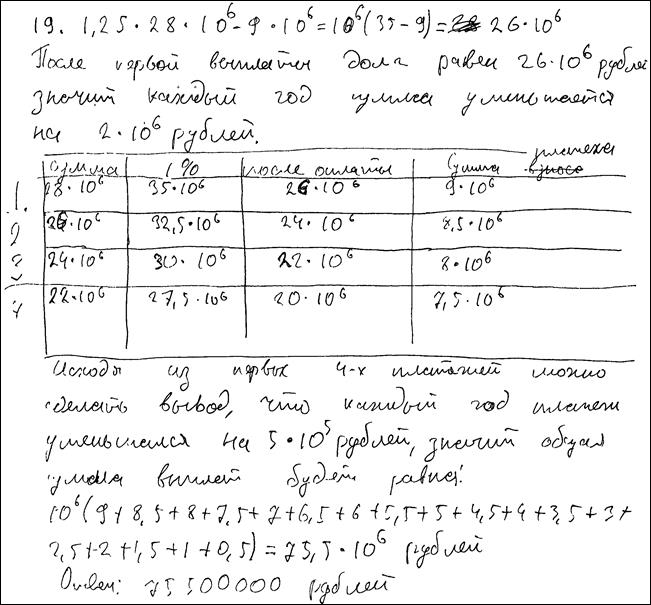
Пример 4. См. задача 3. Кредит = 28 млн рублей. Рост на 25%. Выплаты равномерные, наибольший платеж 9 млн. Чему будет равна общая сумма выплат после полного погашения кредита?

Ответ: 80,5 млн рублей.

Комментарий.

На беглый взгляд – просто вычислительная ошибка, т.е. 2 балла. Смотрим внимательнее. Первые 4 строки заполнены с пониманием дела, разве что нет обоснования того, что именно первая выплата – наибольшая. В целом, верно описана процедура движения финансов: уменьшение долга, уменьшение размеров выплат.

Но, судя по первому столбцу, строчек должно быть 14 (кредит взяли на 14 лет), а у автора, судя по последнему столбцу, их 18. К тому же, есть ошибка в подсчете: 9,5х9 явно больше 75,5.

Оценка эксперта: 1 балл.

Пример 5. См. задача 3. Кредит =9 млн. Рост на 10%. Выплаты равномерные, наибольший платеж 1,5 млн. Чему будет равна общая сумма выплат после полного погашения кредита?

Ответ: 16,2 млн рублей.

Комментарий. Полная и верная бухгалтерская выписка. Можно попробовать «придраться»: а почему именно первая выплата – наибольшая. Но вряд ли возможно снять 1 балл только за это: ведь реализуемость всех условий представлена.

Оценка эксперта: 3 балла.
Пример 6. См. задача 3. Кредит =17 млн. Рост на 10%. Выплаты равномерные, наибольший платеж 3,4 млн. Чему будет равна общая сумма выплат после полного погашения кредита?

Ответ: 26,35 млн рублей.

Комментарий. По внешнему виду – почти то же, что и в Примере 5. Но тут принципиальное непонимание условия: всё время вычитается по 3,4 млн., а в конце – получившийся остаток, меньший 3,4 млн. Скорее всего, автор «переготовился» к ЕГЭ по другой модели «экономической» задачи, с так называемыми «аннуитентными» выплатами.

Источник: megalektsii.ru

Методическая разработка «Решение экономических задач по математике, дифференциальные платежи. ЕГЭ 2020 год».

Экономические задачи «Табличное задание долга или условий начисления процентов» включены в профильный уровень ЕГЭ 2020 год. Учащиеся при подготовки могут самостоятельно рассмотреть и понять алгоритм решения данных задач.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Просмотр содержимого документа
«Методическая разработка «Решение экономических задач по математике, дифференциальные платежи. ЕГЭ 2020 год».»

Экономические задачи

«Табличное задание долга или условий начисления процентов»

Работа учитель математики

высшей квалификационной категории

МКОУ «Кумылженская СШ № 1 им. Знаменского А.Д.»

Пономарёвой Ольги Фёдоровны

1. 15 января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Долг (в % от кредита)

В конце каждого месяца, начиная с января, текущий долг увеличивается на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Пусть взятый полугодовой кредит на развитие бизнеса равен S. По условию задачи заполним таблицу:

Прошло месяцев

Долг на 15-е число

Долг в конце месяца

Общая сумма платежей составила: 0,15S+0,145S+0,14S+0,135S+0,13S+0,525S=1,225S

Общая сумма выплат больше суммы самого кредита на 1,225S ‒ 1S = 0,225S или на 22,5%.

2. Лидия положила некоторую сумму на счёт в банке на полгода. По этому вкладу установлен «плавающий» процент, то есть число начисленных процентов зависит от числа полных месяцев нахождения вклада на счёте. В таблице представлены условия начисления процентов.

Годовая ставка в %

На сколько процентов сумма на счёте Лидии при таких условиях больше суммы, положенной на счёт, если каждый месяц, за исключением последнего, после начисления процентов она добавляет на счёт такую сумму, чтобы за месяц вклад увеличился на 10% от первоначального вклада?

Решаем по простому проценту. Если первые два месяца по 6% годовых, то 6_12=0,5% в месяц, следующие два месяца по 18% годовых, то 18_12=1,5% в месяц, следующие два месяца по 12% годовых, то 12_12=1% в месяц.

Если каждый месяц, за исключением последнего, после начисления процентов Лидия добавляет на счёт такую сумму, чтобы за месяц вклад увеличился на 10% от первоначального вклада, то: пусть изначально Лидия внесла S, тогда каждый месяц прибавляется 0,1S.

Сумма на счету к началу предыдущего месяца

0,005 • 1,1S = 0,0055S

0,015 • 1,2S = 0,018S

0,015 • 1,3S = 0,0195S

0,01 • 1,4S = 0,014S

0,01 • 1,5S = 0,015S

Итого банк начислит: (0,005 + 0,0055 + 0,018 + 0,0195 + 0,014 + 0,015)S = 0,077 S

Данная сумма составит: 0,077 S : S • 100 = 7,7%

На 7,7% сумма на счёте Лидии при таких условиях больше суммы, положенной на счёт.

3. Оксана положила некоторую сумму на счёт в банке на полгода. По этому вкладу установлен «плавающий» процент, то есть число начисленных процентов зависит от числа полных месяцев нахождения вклада на счёте. В таблице представлены условия начисления процентов.

Годовая ставка в %

На сколько процентов сумма на счёте Оксаны при таких условиях больше суммы, положенной на счёт, если каждый месяц, за исключением последнего, после начисления процентов она добавляет на счёт такую сумму, чтобы за месяц вклад увеличился на 5% от первоначального вклада?

Решаем по простому проценту. Если первые два месяца по 12% годовых, то 12_12=1% в месяц, следующие два месяца по 15% годовых, то 15_12=1,25% в месяц, следующие два месяца по 18% годовых, то 18_12=1,5% в месяц.

Если каждый месяц, за исключением последнего, после начисления процентов Оксана добавляет на счёт такую сумму, чтобы за месяц вклад увеличился на 5% от первоначального вклада, то: пусть изначально Оксана внесла S, тогда каждый месяц прибавляется 0,05S.

Сумма на счету к началу предыдущего месяца

Источник: kopilkaurokov.ru

Блог Олега Кривошеина

Стихи и цветы,поздравления и сценарии. Школьная математика, подготовка к ЕГЭ и ГИА,тесты, проекты,задачи и решения. Собственные произведения и фотографии моих цветов: георгины и розы.

Страницы блога

Добро пожаловать в блог! Здесь вы можете поглубже познакомиться с математикой, порешать задания ГИА и ЕГЭ, а в перерывах почитать стихи и посмотреть чудесные цветы. Удачи Вам!

суббота, 14 апреля 2018 г.

Примеры оценивания решений задания 17

Продолжение поста Критерии оценивания заданий №17 ЕГЭ по математике
Пример 1.

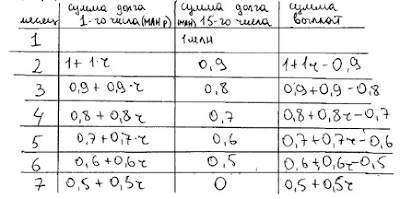
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

(в млн рублей)
Найдите наименьшее значение r , при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

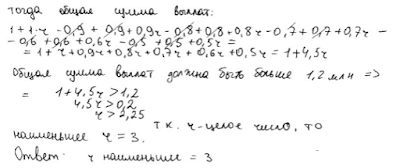
Комментарий.

Модель построена неверно. Если подставить вместо r число 3 в таблицу, то сумма долга уже на 1 число второго месяца должна составить 4 млн рублей, кроме того, еще и неравенство решено неверно.

Оценка эксперта: 0 баллов.
Пример 2.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

(в млн рублей)
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

Комментарий.

Модель построена верно. Усложняет проверку отсутствие вычислений. В таблице все результаты вычислений по формулам, записанным справа, верные. Логика решения верна.

Оценка эксперта: 3 балла.
Пример 3.

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

Источник: krivoleg.blogspot.com