Цель работы:изучение современных программных средств решения задачи линейного программирования; практическое решение задач линейного программирования графическим методом, симплекс-методом и средствами программыMicrosoftExcel; программная реализация симплекс-метода на языке программирования высокого уровня.
1. Теоретическая часть
Для решения задач линейного программирования в программе Microsoft Excel имеется надстройка Поиск решения, обращение к которой производится из меню Сервис.
Если команда Поиск решения отсутствует в меню Сервис, то требуется установить надстройку «Поиск решения». Для этого в меню Сервис выбирается команда Надстройки, которая открывает диалоговое окно, показанное на рис. 1.
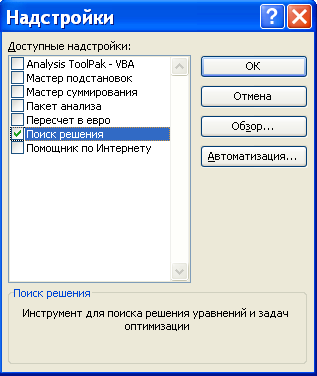
Далее в этом окне устанавливается флажок той надстройки, которую необходимо загрузить, и нажимается кнопка OK.
Покажем использование надстройки «Поиск решения» на примере решения следующей задачи.
Зачем ставить доллар в формулах excel
Постановка задачи
Предприятие изготавливает и реализует три вида продукции – P1, Р2 и Р3. Для производства продукции используются три вида ресурсов – комплектующие изделия, сырье и материалы. Запасы ресурсов и их расход на изготовление единицы продукции каждого вида приведены в табл. 1.
Расходы ресурсов на 1 ед. продукции
Прибыль от реализации единицы продукции каждого вида составляет 240, 210 и 180 денежных единиц для P1, Р2 и Р3 соответственно.
Требуется определить производственную программу предприятия таким образом, чтобы прибыль от реализации продукции была максимальной.
Математическая модель задачи
Обозначим переменными x1, x2 и x3 искомые объемы производства продукции видов P1, Р2 и Р2, а через F – прибыль предприятия. Тогда математическая постановка представленной задачи принимает следующий вид.
Определить значения переменных x1, x2 и x3, для которых достигается максимум целевой функции
F = 240 x1 + 210 х2 + 180 x3
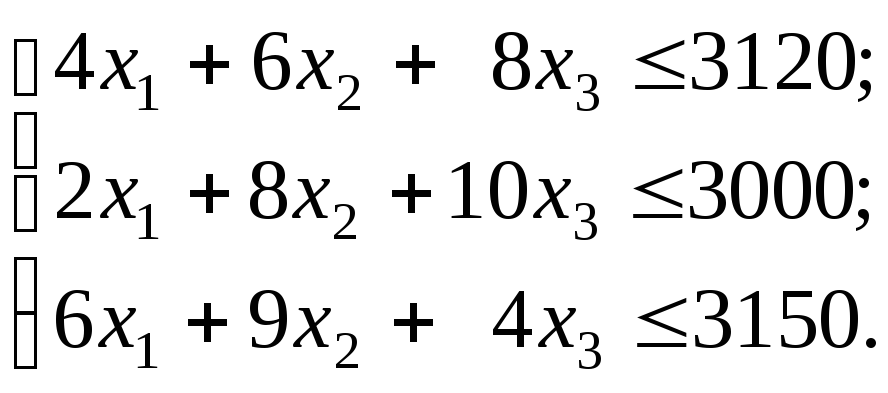

Целевая функция описывает суммарную прибыль от реализации произведенной продукции всех трех видов. Ограничения (1), (2) и (3) учитывают расход и запасы комплектующих изделий, сырья и материалов соответственно. Поскольку объемы производства продукции не могут быть отрицательными, добавляются условия
Порядок оптимального решения задачи
Примерные действия, необходимые для решения задачи линейного программирования средствами программы Excel, представим в виде последовательности шагов.
Шаг 1. Исходные данные задачи записываются на рабочем листе электронной таблицы. Один из вариантов показан на рис. 2.

Замечание. Если известно исходное допустимое базисное решение, то можно несколько ускорить процесс поиска оптимального решения. Для этого начальные значения некоторых или всех переменных могут быть заданы вручную. В данном примере для их хранения используются ячейки $B$2, $C$2 и $D$2. Если допустимое базисное решение не задано, то программа Excel автоматически определяет начальные значения переменных задачи.
ФУНКЦИЯ ВПР В EXCEL, КАК ПОДСТАВИТЬ СРАЗУ ВСЕ ЗНАЧЕНИЯ?
Шаг 2. В ячейку E3 вводится формула
для вычисления текущего значения целевой функции, которая находит сумму попарных произведений ячеек (В3:D3) с коэффициентами при переменных в выражении целевой функции на ячейки ($B$2:$D$2) с текущими значениями переменных.
Шаг 3. Чтобы задать ограничения решаемой задачи, в ячейки E5, E6 и E7 копируется формула из ячейки E3. После этого в указанных ячейках должны быть получены формулы, представленные в табл. 2.
Шаг 4. После создания таблицы с исходными данными курсор устанавливается в ячейку E3, содержащую формулу для вычисления целевой функции. Далее в меню Сервис выбирается команда Поиск решения, которая открывает диалоговое окно, приведенное на рис. 3.

В поле Установить целевую ячейку окна «Поиск решения», показанного на рис. 3, должен появиться адрес ячейки с формулой целевой функции (в данном примере это ячейка $E$3).
Затем в этом окне (рис. 3) заполняются следующие поля этого окна:
— в поле Равной переключатель вида экстремума целевой функции устанавливается в положение максимальное значение (или минимальное значение при соответствующей постановке задачи);
— в поле Изменяя ячейки указывается диапазон ячеек со значениями переменных задачи, выделяемый на рабочем листе электронной таблицы (в примере это ячейки $B$2:$D$2);
— в поле Ограничения задаются ограничения исходной задачи. Для этого курсор устанавливается в поле ввода ограничений и нажимается кнопка Добавить. В результате выводится диалоговое окно «Добавление ограничения», показанное на рис. 4.

В этом окне в поле Ссылка на ячейку вводится адрес ячейки с формулой соответствующего ограничения (например, для ограничения (1) это будет ячейка E5), а в поле Ограничение указывается предельное значение, которое может принимать выбранное ограничение (в данном примере правая часть ограничения (1) находится в ячейке G5).
Следует заметить, что заполнение полей Ссылка на ячейку и Ограничение в окне «Добавление ограничения» можно выполнить выделением соответствующих ячеек рабочего листа электронной таблицы.
Затем выбирается вид отношения, связывающего левую и правую части ограничения, что показано на рис. 5.

После нажатия кнопки Добавить в окне «Добавление ограничения» (или кнопки ОК для ввода последнего ограничения) данное ограничение попадает в список ограничений решаемой задачи. С помощью кнопок Удалить и Изменить можно удалять выделенные в списке ограничения или вносить в них исправления.
Замечание. В окне «Добавление ограничения» можно указать, что все или некоторые переменные должны принимать только целые значения (рис. 5). Это позволяет получать решения задач целочисленного линейного программирования (полностью или частично целочисленных).
Шаг 5. После заполнения всех полей окна «Поиск решения» нажимается кнопка Параметры (рис. 3), которая открывает диалоговое окно «Параметры поиска решения», показанное на рис. 6.

В этом окне требуется установить флажки Линейная модель для решения задачи линейного программирования и Неотрицательные значения, если такое условие накладываются на все переменные задачи.
Здесь (рис. 6) также можно определить параметры процесса решения: предельное время поиска решения, максимальное количество итераций, точность и т.п. Флажок Показывать результаты итераций позволяет по шагам следить за поиском решения. Флажок Автоматическое масштабирование включается в том случае, когда разброс значений переменных очень велик.
Шаг 6. Задав необходимые параметры в окне «Параметры поиска решения», следует нажать на кнопку Выполнить для поиска решения задачи (рис. 3) в окне «Поиск решения». Если решение найдено, то на экран выводится окно с соответствующим сообщением (рис. 7).
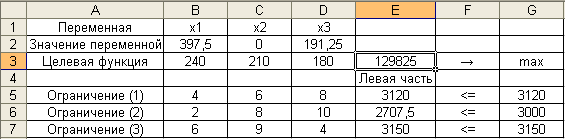
Полученные результаты отображаются на рабочем листе электронной таблицы, как это показано на рис. 8. В частности, значения переменных — в ячейках $B$2:$D$2, значение целевой функции – в ячейке E3.
Таким образом, получено оптимальное решение исходной задачи в виде вектора 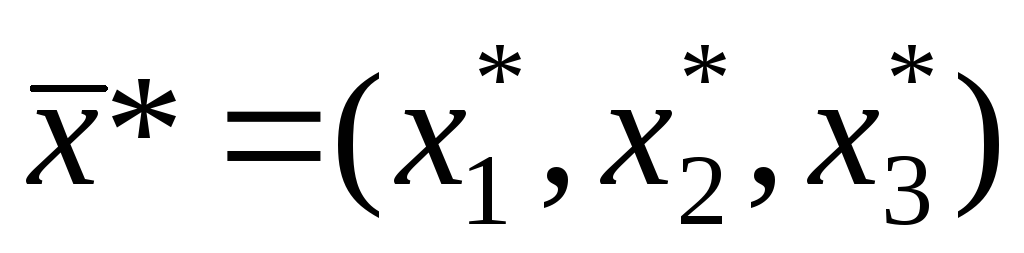 , где
, где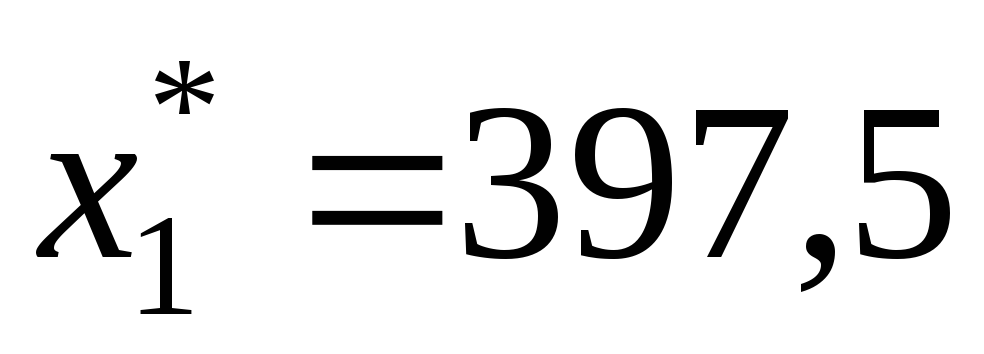 ,
, и
и , для которого значение целевой функцииF максимально и составляет F* = 129825.
, для которого значение целевой функцииF максимально и составляет F* = 129825.
Результаты решения задачи линейного программирования также можно сохранить в виде отдельных рабочих листов с именами Отчет по результатам, Отчет по устойчивости и Отчет по пределам. Для сохранения результатов в виде отчетов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов (рис. 7). В этом же окне можно отказаться от полученных решений и восстановить исходные значения переменных.
Отчет по результатам для рассмотренной задачи показан на рис. 9.
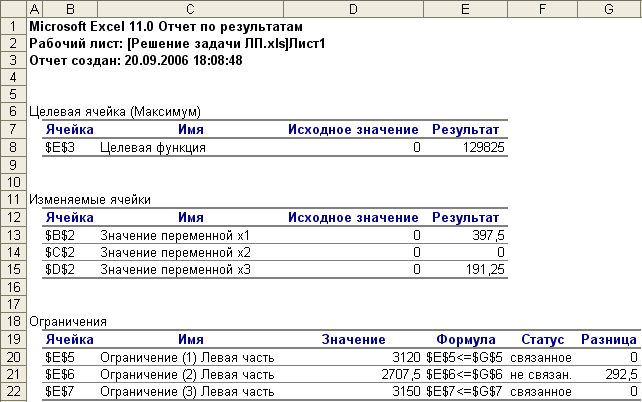
В данном отчете представлены оптимальное решение задачи линейного программирования и его расположение в области допустимых решений. В графах Результат выводятся оптимальные значения целевой функции F* и переменных задачи 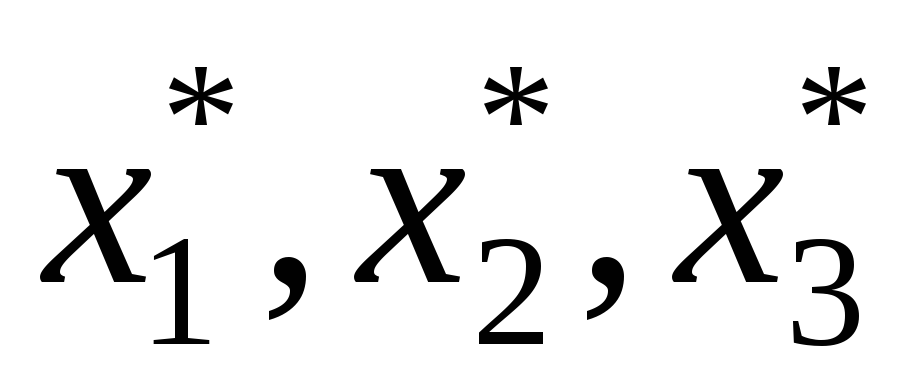 , а также их значения для исходного базисного решения, с которого начинался поиск оптимального решения (графаИсходное значение).
, а также их значения для исходного базисного решения, с которого начинался поиск оптимального решения (графаИсходное значение).
Состояние ограничений (графа Статус) характеризует расположение точки 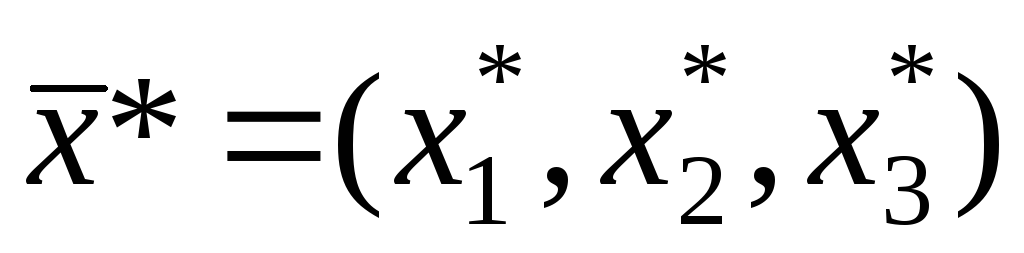 в области допустимых решений. ГрафаРазница показывает разности между значениями левых и правых частей ограничений (невязки). Для связанного ограничения невязка равна нулю, что свидетельствует о расположение точки
в области допустимых решений. ГрафаРазница показывает разности между значениями левых и правых частей ограничений (невязки). Для связанного ограничения невязка равна нулю, что свидетельствует о расположение точки  на границе области допустимых решений, которая задается этим ограничением. Если ограничение являются не связанным, то оно не влияет на оптимальное решение.
на границе области допустимых решений, которая задается этим ограничением. Если ограничение являются не связанным, то оно не влияет на оптимальное решение.
Замечание. В экономической интерпретации связанные ограничения соответствуют дефицитным ресурсам. Для не связанных ограничений графа Разница показывает оставшиеся объемы неиспользованных не дефицитных ресурсов. В рассмотренной задаче ограничения (1) и (3) соответствуют комплектующим изделиям и материалам, которые являются дефицитными ресурсами.
Ограничение (2) является не связанным, т.е. не влияет на оптимальный план производства продукции по критерию максимальной прибыли. Это означает, что второй ресурс (сырье) не использован в объеме 292,5 ед.
В отчете по устойчивости (рис. 10) приведены границы устойчивости переменных задачи (графы Допустимое увеличение и Допустимое уменьшение коэффициентов целевой функции), а также границы устойчивости теневых цен (т.е. переменных двойственной задачи), в пределах которых оптимальное решение не изменяется. Большие значения пределов (1Е+30) означают фактическое отсутствие соответствующих границ, т.е. переменная может изменяться до бесконечности.
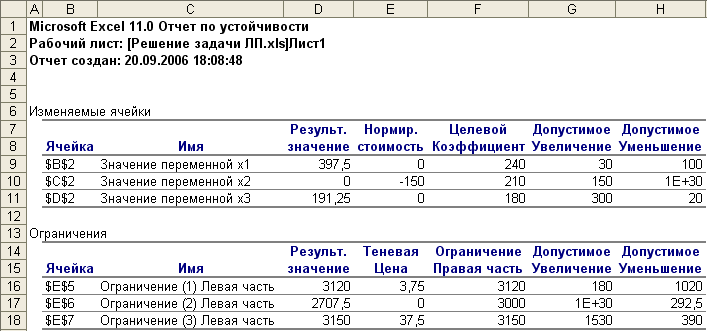
В графе Нормированная стоимость элемент во второй строке (-150) показывает, на сколько уменьшится значение функции, если в решении переменную x2 увеличить на единицу. С другой стороны, при допустимом увеличении коэффициента функции при неизвестной x2 на 150 единиц значение этой переменной не изменится, т.е. неизвестная x2 будет равна нулю, а если выйти за пределы допустимого увеличения (коэффициент при x2 увеличить более чем на 150), то неизвестная x2 в решении будет больше нуля.
В отчете по пределам (рис. 11) показаны нижние и верхние пределы возможного изменения переменных (в пределах области допустимых решений) и соответствующие значения целевой функции (графа Целевой результат) при этих изменениях. В частности, если x1 = 0, а x2 и x3 остаются без изменений, то F = 2400 + 2100 + 180191,25 = 34425; при x3 = 0 и неизменных x1 и x2 получим F = 240397,5 + 2100 + 1800 = 95400.
Источник: studfile.net
Бизнес-анализ в MS Excel

Бизнес-анализ в MS Excel (план лекций):
1. Итоговые таблицы. Сводные таблицы;
2. Финансовые функции и таблицы данных;
3. Решение оптимизационных задач. Использование
инструмента «Поиск решения»;
4. Проверка различных возможностей с помощью
сценариев;
5. Сортировка данных. Фильтрация данных;
6. Создание макросов.
7/15/2018, слайд 2
3. ИТ в экономике
2.1.
Решение
оптимизационных
задач.
Использование инструмента «Поиск решения»
7/15/2018, слайд 3
4. Решение оптимизационных задач
«Поиск решения» – это надстройка для Microsoft Excel,
которую можно использовать для анализ «что если».
С ее помощью можно найти оптимальное значение
(максимум или минимум) формулы, содержащейся в одной
ячейке, называемой целевой, с учетом ограничений на
значения в других ячейках с формулами на листе.
Надстройка «Поиск решения» работает с группой ячеек,
называемых ячейками переменных решения или просто
ячейками переменных, которые используются при расчете
формул в целевых ячейках и ячейках ограничения.
7/15/2018, слайд 4
5. Решение оптимизационных задач
Надстройка «Поиск решения» изменяет значения в
ячейках переменных решения согласно пределам ячеек
ограничения и выводит нужный результат в целевой
ячейке.
Таким образом, с помощью надстройки «Поиск
решения»
можно
определить
максимальное
или
минимальное значение одной ячейки, изменяя другие
ячейки.
Например, вы можете изменить планируемый бюджет на
рекламу и посмотреть, как изменится планируемая сумма
прибыли.
7/15/2018, слайд 5
6. Решение оптимизационных задач
Так как «Поиск решения» – это программная
надстройка для Microsoft Office Excel, ее нужно сначала
загрузить в Excel.
Кнопка Office – Параметры Excel – Надстройки –
Поиск решения – Перейти – Поиск решения – ОК
7/15/2018, слайд 6
7. Решение оптимизационных задач
Поиск решения – Данные – Поиск решения
7/15/2018, слайд 7
8. Решение оптимизационных задач
Задача (практическая работа 3):
Фирма производит две модели А и В сборных книжных полок. Их
производство ограничено наличием сырья (высококачественных досок) и
временем машинной обработки.
Для каждого изделия модели А требуется 3 м2 досок, а для изделия модели
В – 4 м2. Фирма может получать от своих поставщиков до 1700 м2 досок в
неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а
для изделия модели В – 30 мин. В неделю можно использовать 160 ч
машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю,
если каждое изделие модели А приносит 2 долл. прибыли, а каждое изделие
модели В – 4 долл. прибыли.
7/15/2018, слайд 8
9. Решение оптимизационных задач
Математическая модель
Обозначим:
x – количество изделий модели А, выпускаемых в течение
недели,
y – количество изделий модели В.
Прибыль от этих изделий равна 2x+4y долл. Эту
прибыль нужно максимизировать.
Функция, для которой ищется экстремум (максимум или
минимум), носит название целевой функции.
7/15/2018, слайд 9
10. Решение оптимизационных задач
Математическая модель
Беспредельному
увеличению
количества
изделий
препятствуют ограничения.
Ограничено количество материала для полок:
3x+4y 1700.
Ограничено машинное время на изготовление полок (на
изделие А уходит 0,2 часа, на изделие В – 0,5 часа):
0,2x+0,5y 160
Кроме того, количество изделий – неотрицательное и
целое число, поэтому: x 0, y 0 и x, y — целые.
7/15/2018, слайд 10
11. Решение оптимизационных задач
Математическая модель
Формально задача оптимизации записывается так:
2 x 4 y max
3 x 4 y 1700
0,2 x 0,5 y 160
x 0, y 0
x, y целые
7/15/2018, слайд 11
12. Решение оптимизационных задач
Решение задачи в MS Excel
7/15/2018, слайд 12
13. Решение оптимизационных задач
Решение задачи в MS Excel
7/15/2018, слайд 13
14. Решение оптимизационных задач
Решение задачи в MS Excel
7/15/2018, слайд 14
15. Решение оптимизационных задач
Решение задачи в MS Excel
Вид таблицы меняется: в ячейках Е2 и Е3 появляются оптимальные
значения: изделие А нужно выпускать в количестве 300 штук в неделю, а
изделие В – 200 штук. Соответственно пересчитываются все формулы. Целевая
функция достигает значения 1400.
7/15/2018, слайд 15
16. Решение оптимизационных задач
Задача (практическая работа 3):
Фабрика выпускает два типа красок – для внутренних и наружных работ. Для
производства красок используется три исходных продукта – А, В и С. Объем емкостей
для хранения суточных запасов этих продуктов равен соответственно 4, 6 и 8 тонн.
Расходы продуктов приведены в таблице:
Исходный продукт
А
В
С
Расход исходных продуктов
(в тоннах) на единицу краски
Краска внутр.
Краска наружн.
1
1,3
1,5
1
2
2,1
Максимально
возможный запас
4
6
8
Изучение рынка показало, что суточный спрос на краску Квн никогда не
превышает спрос на краску Кнаруж более чем на 1,5 тонны. Кроме того,
исследования показали, что спрос на краску Кнаруж никогда не превышает 2,4 тонн
в сутки. Продажные цены для красок (за тонну): Кнаруж= 4500 руб., Квн= 4100 руб.
Какое количество краски каждого вида должна производить фабрика, чтобы
доход от реализации был максимальным?
7/15/2018, слайд 16
17. Решение оптимизационных задач
Математическая модель
Цель – получение максимальной прибыли.
Обозначим:
Хнаруж – суточный объем производства краски Кнаруж и
Хвн – суточный объем производства краски Квн.
Суммарная суточная прибыль от производства красок:
S 4500 * xнаруж 4100 * xвн
Таким образом, необходимо определить среди всех
допустимых значений Хнаруж и Хвн те, которые
максимизируют суммарную прибыль, т.е. целевую функцию.
S.
7/15/2018, слайд 17
18. Решение оптимизационных задач
Ограничения:
1. Объем
производства
красок
не
может
быть
xнаруж , xв н 0
отрицательным:
2. Расход исходного продукта для производства красок не
может превосходить максимально возможный запас:
1* xв н 1,3 * xнар 4
1,5 * xв н 1* xнар 6
2 * xв н 2,1* xнар 8
3. Ограничения на величину спроса на краски имеют вид:
xвн xнар 1,5
xнар 2,4
7/15/2018, слайд 18
19. Решение оптимизационных задач
Решение задачи в MS Excel
7/15/2018, слайд 19
20. Решение оптимизационных задач
Решение задачи в MS Excel
Доход от производства краски будет максимальным, если
в день производится 2,4 тонны краски для внутренних работ
и 1,23 тонны краски для наружных работ.
7/15/2018, слайд 20
21. Решение оптимизационных задач
Задача (практическая работа 3):
Фирма по производству моющих средств рекламирует свою продукцию в
Интернете, по телевидению, на радио и в печатных изданиях. Затраты на рекламу
ограничены 10000$ ежемесячно. При этом один блок рекламы по телевидению стоит
в 10 раз дороже, чем по радио, в 5 раз дороже, чем в печатных изданиях и в 50 раз
дороже рекламы по Интернету. При этом исследования показали, что эффективность
рекламы по Интернету в 3 раза выше, чем в печатных изданиях и в 2 раза
эффективнее, чем по радио. Рекламировать товар необходимо во всех источниках
средств массовой информации. Определите ежемесячное оптимальное распределение
вложений в рекламу.
7/15/2018, слайд 21
22. ИТ в экономике
2.2. Проверка различных возможностей с помощью
сценариев
7/15/2018, слайд 22
23. Проверка различных возможностей с помощью сценариев
Сценарий – это набор значений, которые Excel сохраняет
и может автоматически подставлять на листе.
Можно создать и сохранить различные группы
значений в виде сценариев, а затем переключаться на
любой из них, чтобы просматривать различные результаты.
После подготовки всех нужных сценариев можно создать
сводный отчет, в который включаются данные из всех
сценариев.
7/15/2018, слайд 23
24. Проверка различных возможностей с помощью сценариев
Задача (практическая работа 4):
Построить модель прогноза продаж на несколько лет.
Особое
внимание следует
обратить
на
адресацию ячеек
7/15/2018, слайд 24
25. Проверка различных возможностей с помощью сценариев
Использование сценариев:
Данные – Анализ «что если» – Диспетчер сценариев
7/15/2018, слайд 25
26. Проверка различных возможностей с помощью сценариев
Предположим, необходимо создать три сценария для
приведенной модели: наилучший прогноз, наилучший
результат, наихудший результат. Эти оценки дадут
общую картину возможностей в будущем.
Рассмотрим наихудший результат:
12% для Продаж,
14% для Стоимости проданных товаров,
18% для Общих и административных расходов,
20% для Маркетинга.
7/15/2018, слайд 26
27. Проверка различных возможностей с помощью сценариев
На вкладке Данные выберите команду Анализ «что если»
– Диспетчер сценариев.
Появится диалоговое окно Диспетчер сценариев:
7/15/2018, слайд 27
28. Проверка различных возможностей с помощью сценариев
Для создания дополнительных сценариев нажмите кнопку
Добавить и повторите действия.
Создайте сценарий Наилучшая оценка (15% для
Продаж, 15% для Стоимости проданных товаров, 12% для
Общих и административных расходов и 17 % для
Маркетинга) и Наилучший результат (20% для Продаж,
18% для Стоимости проданных товаров, 18% для Общих и
административных расходов и 19 % для Маркетинга).
В окне Диспетчера сценариев будут перечислены три
сценария.
7/15/2018, слайд 28
29. Проверка различных возможностей с помощью сценариев
Просмотр сценария
Выберите название сценария, который необходимо
просмотреть: Наилучший результат.
Нажмите кнопку Вывести. На экране изменятся значения
столбца $D$15:$D$18 и пересчитанная исходная таблица.
7/15/2018, слайд 29
30. Проверка различных возможностей с помощью сценариев
Создание итогового отчета по сценариям
На вкладке Данные выберите команду Анализ «что если»
– Диспетчер сценариев. Нажмите кнопку Отчет. Появится
диалоговое окно Отчет по сценарию. Установите
переключатель в положение Структура.
7/15/2018, слайд 30
31. Проверка различных возможностей с помощью сценариев
Создание отчета по сценариям в виде сводной таблицы
На вкладке Данные выберите команду Анализ «что если»
– Диспетчер сценариев. Нажмите кнопку Отчет. Появится
диалоговое окно Отчет по сценарию. Установите
переключатель в положение Сводная таблица.
7/15/2018, слайд 31
32. ИТ в экономике
2.3. Фильтрация данных
7/15/2018, слайд 32
33. Фильтрация данных
Фильтрация данных – вывод на экран только тех
записей (строк), которые отвечают определенному критерию
(условию).
Виды фильтрации:
• автофильтр;
• расширенный фильтр.
После фильтрации данных в диапазоне ячеек или
таблице можно применить фильтр повторно для получения
последних данных или очистить фильтр для вывода всех
данных.
7/15/2018, слайд 33
34. Фильтрация данных
Автофильтр: Данные – Фильтр
Возможен отбор по нескольким
столбцам.
Несколько
фильтров
можно
применять одновременно.
Фильтры
действуют
по
дополнительному принципу, т. е.
каждый новый фильтр накладывается
на фильтр, примененный до него, и в
еще большей степени ограничивает
подмножество данных.
7/15/2018, слайд 34
35. Фильтрация данных
Фильтрация данных в таблице
1. Выделите данные, которые нужно отфильтровать. Для
лучшего результата столбцы должны включать заголовки.
2. Щелкните стрелку рядом с заголовком столбца и
выберите пункт Текстовые фильтры или Числовые
фильтры.
3. Выберите один из операторов сравнения.
4. В поле Пользовательский автофильтр введите или
выберите критерии для фильтрации данных.
7/15/2018, слайд 35
36. ИТ в экономике
2.4. Создание макросов
7/15/2018, слайд 36
37. Создание макросов
Макрос – это набор инструкций, которые программа
выполняет по команде запуска.
Инструкции
могут
соответствовать
простым
нажатиям клавиш или сложным наборам команд меню.
Макросы обычно создаются при необходимости в
регулярном
выполнении
операций,
которые
повторяются в одном и том же порядке.
Они записываются на языке программирования Visual
Basic для приложений (for Applications).
7/15/2018, слайд 37
38. Создание макросов
Visual Basic for Applications (VBA) –
это визуальный объектно-ориентированный язык
макропрограммирования высокого уровня, встроенный
во все программы пакета Microsoft Office.
Для создания программ на языке VBA используется
редактор Visual Basic (VBE Visual Basic Editor).
7/15/2018, слайд 38
39. Создание макросов
Выделяют три основные разновидности макросов:
Командные макросы. Основным предназначение
таких макросов является изменение внешнего вида окна
или объекта.
Пользовательские функции – эти макросы работают
аналогичным образом, как встроенные функции Excel.
Макрофункции, представляющие собой сочетание
командных макросов и пользовательских функций.
7/15/2018, слайд 39
40. Создание макросов
Способы создания макросов:
Встроенное
средство
автоматической
макросов – макрорекордер;
Окно редактора Visual Basic.
записи
Обычно при создании сложных макросов объединяют
два этих способа в один.
7/15/2018, слайд 40
41. Создание макросов
В Excel макрос можно сохранить:
в текущем документе;
в новой рабочей книге, чтобы иметь возможность
использовать его из других рабочих книг;
в личной книге макросов.
7/15/2018, слайд 41
42. Создание макросов
Прежде чем создавать макрос надо продумать, какие
действия он должен выполнять и настроить приложение таким
образом, чтобы можно было беспрепятственно выполнить
команды, подлежащие записи. Если этого не сделать, то операции
подготовки к записи макроса также будут записаны в текст
макроса, и в результате этого он будет работать не верно.
Чтобы работать с макросами необходимо в MS Excel добавить
вкладку «Разработчик» (Office – Параметры Excel – Основные
– «Разработчик»).
7/15/2018, слайд 42
43. Создание макросов
Чтобы создать макрос через макрорекордер:
Запустить встроенное средство автоматической записи
макроса: «Разработчик – Код – Запись макроса». Откроется
диалоговое окно «Запись макроса».
Ввести имя макроса и краткое его описание.
Указать место, где будет сохранён макрос.
Задать комбинацию клавиш для вызова макроса.
Щёлкнуть на кнопке ОК, и начнётся запись макроса.
Выполнить действия, которые следует включить в макрос.
После выполнения всех шагов по вводу макроса щёлкнуть на
кнопке «Остановить запись».
7/15/2018, слайд 43
44. Создание макросов
Важно!
При
записи
фиксируются
лишь
выполняемые операции, но не затраченное время,
поэтому торопиться нет необходимости (иначе, ошибка,
так и операции по её исправлению будут воспроизведены
при запуске макроса).
При необходимости отформатировать текст с
помощью макроса параметры форматирования следует
выбирать в соответствующем диалоговом окне, через
меню. На вкладках кнопками пользоваться не стоит,
поскольку они работают как переключатели и результаты
в этом случае будут непредсказуемы.
7/15/2018, слайд 44
45. Создание макросов
Для запуска макроса:
Вызвать команду «Разработчик – Код – Макросы»;
Выбрать в списке нужный макрос;
Щёлкнуть на кнопке «Выполнить».
Удаление макросов (двумя способами):
Переписать макрос заново под тем же именем, если
не устраивает работа первоначального макроса;
Вызвать команду «Разработчик – Код – Макросы –
выбрать необходимый макрос и щёлкнуть на кнопке
Удалить».
7/15/2018, слайд 45
46. Создание макросов
Задача (практическая работа 6):
Создать макросы для построения сводных таблиц.
Назначить их элементу управления Список.
7/15/2018, слайд 46
47. Создание макросов
Для таблицы на рабочем листе Отправленная_кор необходимо:
1. составить ежедневный отчет о весе посылок для каждого
направления, используя сводную таблицу; сводную таблицу
расположить на листе Сводная_таблица; создать макрос
Вес_корр.
2. создать макрос, который удаляет сводную таблицу любого
размера (начиная с первой ячейки расположения сводной
таблицы).
3. составить отчет о стоимости корреспонденции для каждого
направления, используя сводную таблицу; сводную таблицу
расположить на листе Сводная_таблица; создать макрос
Стоимость_корр.
7/15/2018, слайд 47
48. Создание макросов
Назначить макросы Удалить_св_табл, Вес_корр
Стоимость_корр элементу управления «Список».
и
7/15/2018, слайд 48
Источник: ppt-online.org
Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.
Основные параметры поиска решений
Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.
Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:
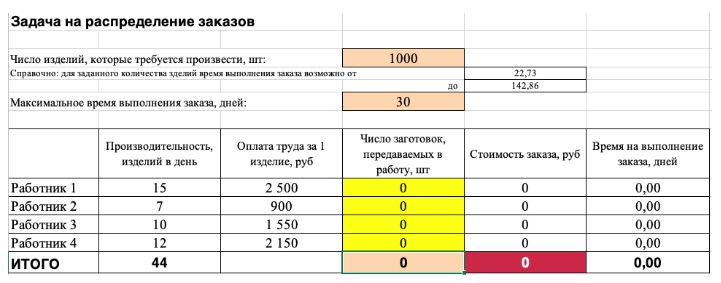
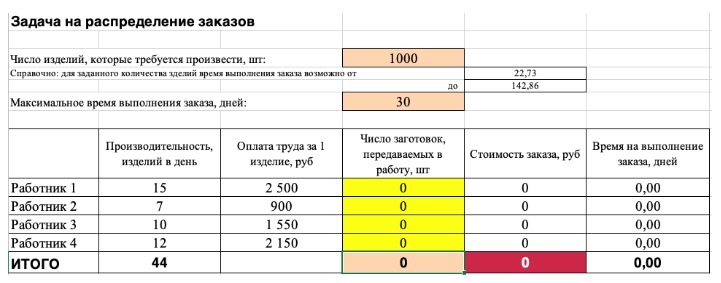
Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).
Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.
Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.
Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.
Пример использования поиска решений
Теперь перейдем к самой функции.
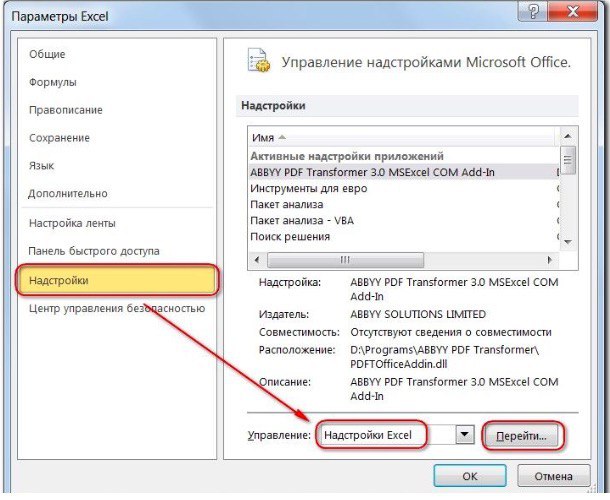
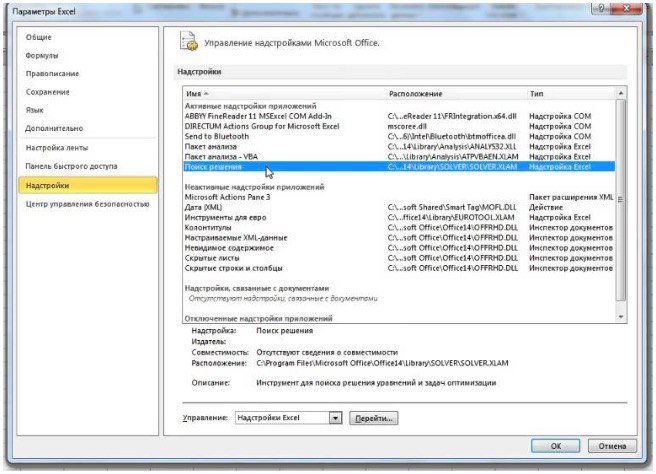
1) Чтобы включить «Поиск решений», выполните следующие шаги:
- нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
- в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
- в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.
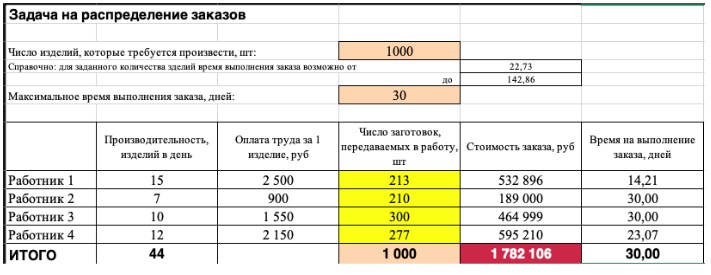
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым — изменяемые ячейки.
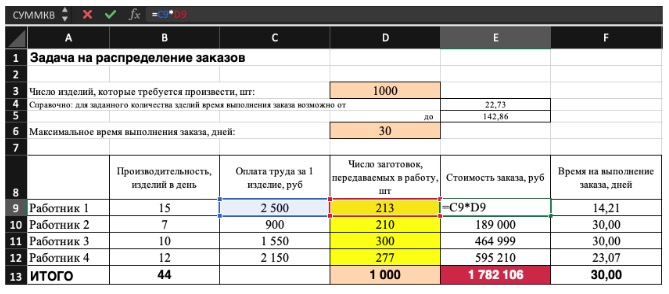
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».
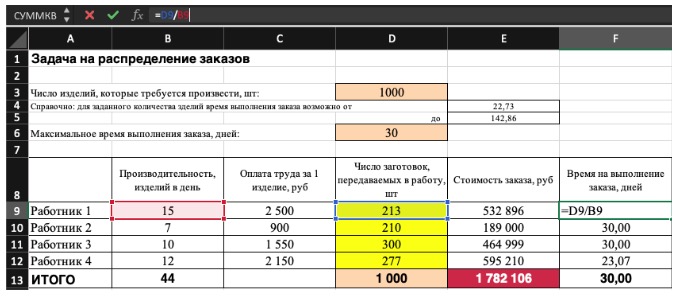
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).
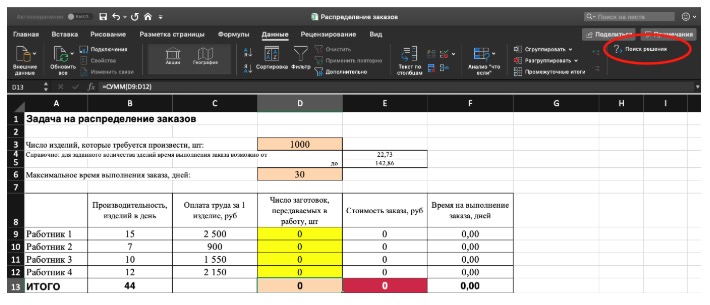
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».
Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.
В нашем примере следующие ограничения:
- общее количество изделий 1000 штук ($D$13 = $D$3);
- число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
- количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).
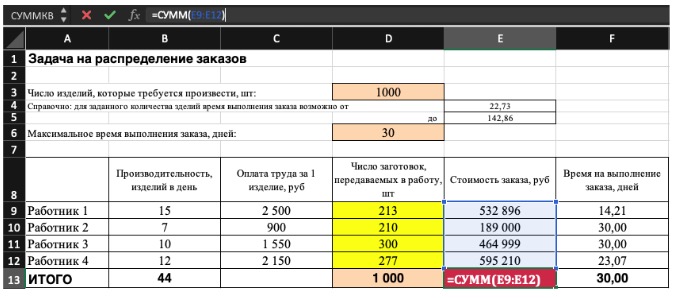
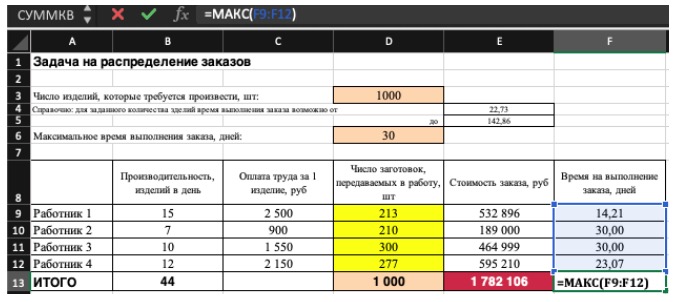
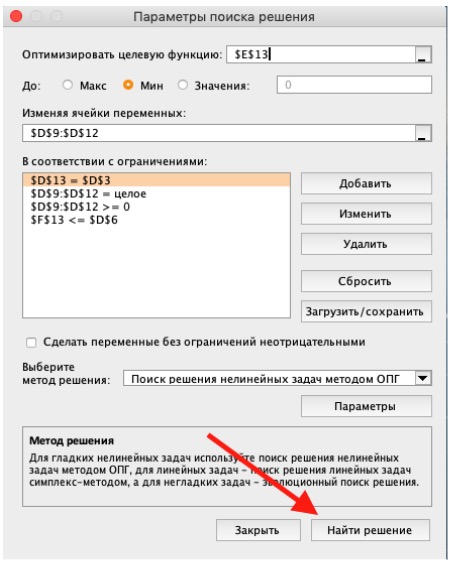
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.
Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!
Теги
Получите карьерную поддержку
Если вы не знаете, с чего начать карьеру, зашли в тупик или считаете, что совершили какие-то ошибки, спросите совета у специалистов. Заполните заявку и консультанты Changellenge >> окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.
Подписаться на карьерную рассылку
Подписывайтесь на рассылку и получайте карьерные советы — от выбора индустрии и компании до лайфхаков по самоорганизации и развитию коммуникативных навыков.

Стажёр менеджер продукта (Логистика, Отдел продуктовых менеджеров департамента логистика)
Инженер по радиоизмерениям

Менеджер-стажер по работе с клиентами

Стажер-консультант по управлению персоналом
Business Development Manager

Стажер отдела аудиторских услуг

Стажер группы невыездного аудита

Стажер отдела по работе с клиентами
Источник: changellenge.com
