

Уставный капитал акционерного общества составляет 60млн.руб. и выпущено 300 обыкновенных акций. Определить номинальную стоимость 1 акции.
60млн.руб./300=200 000 руб
Из зарегистрированных акционерным обществом 30000 обыкновенных акций 29000 продано акционерам. В последующем общество выкупило у владельцев 2500 акций. По итогам года собрание акционеров приняло решение распределить 605млн.руб. чистой прибыли в качестве дивидендов. Определить сумму дивиденда на каждую акцию, находящуюся в обращении.
На основании приведенных данных рассчитать стоимость чистых активов и сделать выводы.
Основные средства – 1500 тыс. руб.; дебиторская задолженность – 920 тыс. руб.; кредиторская задолженность – 860 тыс. руб.; краткосрочные обязательства – 480 тыс. руб.; долгосрочные финансовые вложения – 520 тыс. руб.; нематериальные активы – 1200 тыс. руб., основные средства, переданные в безвозмездное пользование благотворительным фондам – 740 тыс. руб., размер уставного фонда открытого акционерного общества – 14 000 тыс. руб..
Экономические задачи в ЕГЭ 2022 .Вебинар | Математика
Величина чистых активов:
1500 + 920 – 860 – 480 + 520 + 1200 – 740 = 2 060 тыс. руб.
Вывод: в соответствии с Гражданским кодексом Республики Беларусь (ст. 99) стоимость чистых активов предприятия меньше величины его уставного фонда, следовательно оно должно объявить о своей ликвидации.
Определите количество акций акционерного общества, которые оно должно выпустить в обмен на выпускаемые им акции фирмы (т.е. мерджера поглощения). Если рыночная стоимость акций акционерного общества 50уе, рыночная цена акций фирмы 10уе, надбавка включаемая в цену акции фирмы и выплачиваемая акционерным обществом акционерам фирмы, исчисляемая от рыночной цены акций фирмы 15%, общее количество акций фирмы на рынке 200тыс.шт.
Меновое соотношение акций с учетом премии акционерам фирмы Мс ф = 10*1,15/50=0,23
Потребное количество акций акционерного общества Ка = 0,23*200000=46000шт.
Т.о., для проведения мерджера поглощения акционерному обществу достаточно выпустить 46000шт. акций, чтобы выкупить акции выкупаемой фирмы.
Общество с дополнительной ответственностью создано 4-мя учредителями, которые сформировали уставный фонд предприятия в следующих пропорциях: 1 учредитель – 25%; 2 учредитель – 25%; 3 учредитель – 40%; 4 учредитель – 10%.
К концу первого года функционирования уставный фонд был сформирован в полном объеме в соответствии с законодательством. Через три года третий учредитель подал заявление о выходе из состава учредителей с пропорциональным перераспределением его доли между оставшимися участниками. На момент подачи заявления уставный фонд составлял 5 тыс. евро за счет прибыли предприятия.
Определить долю третьего учредителя и размер выплат, которые должны произвести оставшиеся учредители.
Урок 28. Экономика. Решение экономических задач.
1. Доля третьего учредителя на момент выхода:
5 тыс. евро * 0,4 = 2 тыс. евро.
2. Перераспределение долей оставшихся учредителей:
1 учредитель: 0,25 * 100% / (0,25 + 0,25 + 0,10) = 41,7%;
2 учредитель: 0,25 * 100% / (0,25 + 0,25 + 0,10) = 41,7%;
4 учредитель: 0,10 * 100% / (0,25 + 0,25 + 0,10) = 16,6%
3. Выплаты оставшихся учредителей:
1 учредитель: 2 тыс. евро * 41,7% = 834 евро;
2 учредитель: 2 тыс. евро * 41,7 = 834 евро;
4 учредитель: 2 тыс. евро * 16,6% = 332 евро.
Задача 6
Стоимость основных средств предприятия на 1 января планируемого года 120 млн. руб. Планируется ввод в эксплуатацию основных средств – 15 млн. руб. Выбытие основных средств определено на 6 млн. руб. Ввод предусмотрен 1 марта, выбытие – 25 ноября.
Определить среднегодовую величину основных средств в плановом периоде, коэффициенты обновления и выбытия.
Решение:
1. 
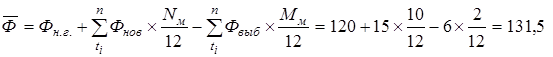 (млн. руб.);
(млн. руб.);
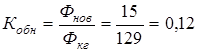
2. ;
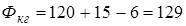
3. (млн. руб.);
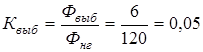
4. .
Задача 7
Стоимость оборудования цеха 15000 млн. руб. С 1 марта введено в эксплуатацию оборудование стоимостью 45,6 млн. руб., с 1 июля выбыло оборудование стоимостью 20,4 млн. руб.
Размер выпуска продукции 800 тонн, цена 1 тонны 30 тыс. руб. Производственная мощность – 1000 тонн.
Определить величину фондоотдачи оборудования и коэффициент интенсивного использования оборудования.
Решение:
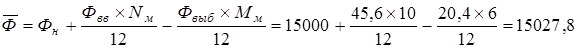
1. (млн. руб.);
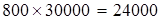
2.Вф в денежном выражении: (млн. руб.);
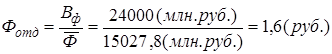
3. ;
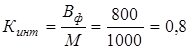
4. .
Задача 8
Чистый вес детали (изделия), изготовленный из стали — 96 кг, норма расхода стали 108 кг. Выпуск 3000 изделий в год. Поставки стали осуществляются один раз в квартал. Транспортный запас – два дня.
Определить величину производственного запаса и коэффициент использования стали.
Решение:
s Определяем производственный запас (Нпр.з)
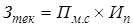
Неизвестное значение Пм.с –среднесуточная потребность стали
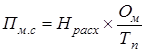
;
где Ом- количество изготавливаемых изделий
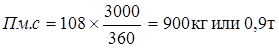
;

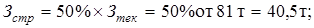

Дн – количество дней транспортного запаса:
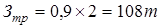
s Определяем коэффициент использования стали (Ки)
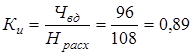
,
где Чвд – чистый вес детали.
Задача 9
В первом квартале предприятие реализовало продукции на 250 млн. руб., среднеквартальные остатки составили 25 млн. руб. Во втором квартале объем реализации продукции увеличился на 10%, а время одного оборота оборотных средств будет сокращено на один день.
s коэффициент оборачиваемости оборотных средств и время одного оборота в днях в первом квартале;
s коэффициент оборотных средств и их абсолютную величину во втором квартале;
s высвобождение оборонных средств в результате сокращения продолжительности одного оборота оборотных средств.
Решение:
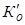
1)Коэффициент оборачиваемости ( ) оборотных средств в первом квартале рассчитает по формуле:
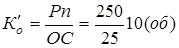
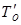
2)Время одного оборота в первом квартале определим по формуле ( ):
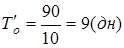
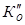
3)Коэффициент оборачиваемости оборотных средств во втором квартале рассчитаем по формуле ( ):
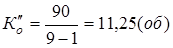
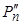
4)Рассчитаем объем реализации продукции во втором квартале ( ):
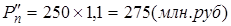
5)Определим абсолютную величину потребности в оборотных средствах во втором квартале:
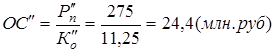
Высвобождение оборотных средств в результате сокращения продолжительности одного оборота определяем по формуле:
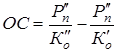
,
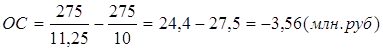
Задача 10
Рассчитать минимальное, но достаточное число рабочих на взаимосвязанных производственных участках цеха, если на первом трудоемкость работ на месяц составляет 4 569 нормо-часов, на втором – 5 860 нормо-часов и третьем – 2 513 норма-часов. Плановое выполнение норм выработки соответственно 118, 124 и 111%, фонд рабочего времени одного рабочего 168 часов в месяц.
Решение
Расчет численности по каждому участку производится по формуле:
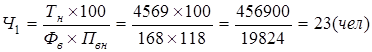
;
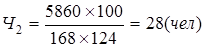
;
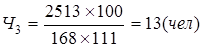
;
Задача 11
Рассчитать профессионально-квалификационный состав бригады и минимальную, но достаточную для выполнения задания численность рабочих в бригаде с учетом совмещения профессий, если нормированная трудоемкость отдельных видов профессий на месяц составляет: слесарно-сборочных по V разряду – 390, по IV разряду – 580, по III разряду – 290 и по II разряду – 483 норма-часов; электросварочных, соответственно, по V и III – 386 и 190 норма-часов. В месяц каждый рабочий отрабатывает 21 день по 8 часов при среднем выполнении норм на 115%.
Решение:
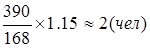
s численность слесарей V разряда составит
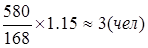
s численность слесарей IV разряда —

s численность слесарей III разряда —
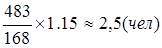
s численность слесарей II разряда —
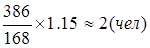
s электросварщиков V разряда —

s электросварщиков III разряда —
При совмещении функций слесаря II разряда (0,5 ставки) со слесарем III разряда общая численность бригады составит 10 человек.
Задача 12
Промышленное предприятие осваивает новое изделие. Планируется выпуск Q =25 тыс. изделий в год. Предполагаемая длительность выпуска этого изделия не более Т=6 лет, после чего изделие морально устареет, и предприятие будет вынуждено снять его с производства. Рыночная цена на это изделие, по какой реально продать всю продукцию Ц (без НДС)=6 тыс.руб.
Периоду выпуска продукции будет предшествовать период освоения производства Тнач.=1 год.
Планируемые затраты предприятия:
- Единовременные инвестиции в размере I 0=50 млн. руб. в самом начале реализации проекта;
- С этого же момента пойдут затраты предприятия на данный инвестиционный проект (включая все налоги и отчисления без НДС), т.е. постоянные ежегодные в размере Зпост.=20 млн. руб. в год;
- С началом выпуска изделия предполагаются переменные затраты в размере З var =2 тыс. руб. на одно изделие.
Определить! Будет ли выгоден проект, если цена капитала (кредитная ставка) равна 30% в год.
Решение:
Представим денежные потоки ( CF ), которые возникают при осуществлении данного проекта по выпуску нового изделия в графической форме. При этом единовременные затраты ( I 0) будут производиться в начале периода освоения продукции в точке отсчета. Постоянные затраты (Зпост.) также будут осуществляться в начале каждого года реализации проекта, а переменные (Зпер.
), связанные с выпуском продукции найдут свое место по окончании каждого года. По окончании каждого года выпуска продукции денежный поток (выручка) от реализации продукции составит: Вреал.= 25∙10 3 ∙6∙10 3 =150∙10 6 руб.в год. При условии, что ежегодная величина переменных затрат Зпер.=З var ∙ Q =2∙10 3 ∙25∙10 3 =50∙10 6 руб.в год график распределения денежных потоков будет выглядеть следующим образом.
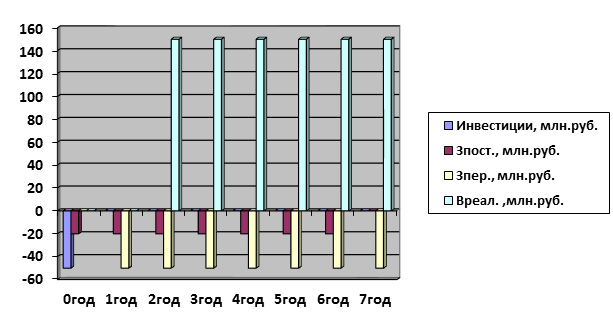
Рисунок 1 График распределения денежных потоков
Для определения выгодности реализации проекта достаточно определить показатель чистой текущей стоимости (ЧТС) проекта при ставке капитала в 30% годовых. Приведем расчет проекта с использованием универсальной табличной формы (Таблица 1). Это один из возможных способов определения показателя ЧТС.
Источник: znanio.ru
Задача с решением по экономике. Формулы по экономике для решения задач



Сегодня мы научимся решать различные задачи по экономике из разных отраслей. Материал будет полезен как тем, кто только начал изучать экономику (и даже тем, кто просто ею интересуется), так и людям, которые уже умеют решать задачи и делают это хорошо. Ведь тренировок много не бывает, а повторение — мать учения. Но перед тем, как показать, как решается та или иная задача по экономике, расскажем как всё начиналось.

История
Существует целая наука, которая называется «История экономики». Она изучает, как со временем менялись хозяйственные отношения между людьми и как эта наука стала такой, какой мы видим её сейчас. Если задуматься, то становится очевидным, что экономическая наука издревле окружает нас.
Например, даже в первобытном обществе существовал так называемый «натуральный обмен» — то есть люди меняли свои вещи на другие без использования денег. Постепенно появляется денежный эквивалент, роль которого исполняет золото. До сих пор запасы многих стран оцениваются в золотом эквиваленте.
Сначала золоту и другим драгоценным металлам придавали форму слитков, но затем в Древней Греции и Древнем Риме начали чеканиться монеты. Монеты долгое время подразделялись на золотые, серебряные и бронзовые. В конце концов мы пришли к той валюте, что видим сейчас.
Виды задач
Сейчас мы разберём виды, а затем примеры и решение задач по экономике, с ответами на которые вы можете ознакомиться в конце статьи. Для начала разберёмся, какие виды задач бывают. Их различают по отраслям, в каждой из которых свои формулы для вычисления. Различают экономику предприятия, экономику труда, экономическую статистику, макро- и микроэкономику. Поговорим немного обо всех этих отраслях.
Для начала разберём такую отрасль, как экономика организации. Задачи с решениями вы можете найти ниже.
Экономика предприятия
Этот раздел тесно связан с макро- и микроэкономикой. Экономика предприятия изучает его структуру, особенности производственного цикла, формирование основных средств и оборотных фондов, разрабатывает стратегию производства и в целом организует управление организацией. Основной целью этой сферы является достижение максимальной прибыли при минимальных расходах, а также оптимизация деятельности производства. Экономика предприятия изучает также деятельность компании и положение её на рынке, анализирует способы увеличения и стабилизации прибыли. Это следует помнить при решении задач на данную тему.
На самом деле нет ничего сложного в том, чтобы понять, как работает экономика организации. Задачи с решениями, кстати, вы можете найти немного ниже.

Экономика труда
Можно сказать, что эта сфера является подразделом предыдущей, однако это не совсем так. Экономика труда анализирует рынок труда, занимается изучением взаимодействия работников и набором персонала. Это тоже, несомненно, важная часть науки, которую необходимо изучать. Экономика труда играет ключевую роль в управлении предприятием. Ведь без сотрудников не может быть производства товара.
Экономическая статистика
Этот раздел занимается исследованием статистических данных экономических процессов. В теоретической части статистика опирается на экономическую теорию и анализирует процессы в какой-либо области с помощью её законов. Она тесно связана с экономическим анализом и социально-демографической статистикой.

Макроэкономика
Предметом исследования макроэкономики являются крупные экономические проблемы и события. Она создана для анализа и выявления закономерностей в таких показателях, как общий национальный доход, уровень цен и занятости. Фактически, она объединяет в себе более мелкие процессы и рассматривает их в общем. Поэтому в некоторых подразделах для решения задач можно применять макроэкономический подход.

Микроэкономика
Микроэкономический анализ можно рассмотреть как инструмент, который позволяет объяснить, как принимаются управленческие экономические решения на низшем уровне. Если макроэкономика рассматривает решения на высшем уровне, скажем, на уровне государства, то микроэкономика позволяет провести анализ на уровне конкретного предприятия.

Формулы по экономике
Для решения задач нам понадобятся некоторые теоретические знания и формулы. Мы можем разделить их по отраслям применения, и начнём с экономики предприятия. Начнём с показателя рентабельности. Он показывает, как относятся между собой прибыль предприятия и среднегодовая стоимость основных средств. Математически это можно выразить так: R=П/Ссг.
Ответ мы получаем в долях единицы, а если хотим получить процент рентабельности, нужно домножить получившуюся величину на 100%. Также рассматривают такие показатели, как фондоотдача (Фотд), Фондоёмкость (Фёмк), и Фондовооружённость (Фвоор). Их вычисление тоже не составляет труда: Фотд=N/Ссг , где N — объём реализованной продукции; Фёмк=1/Фотд; Фвоор=Ссг/Чраб, где «Чраб» — численность рабочих (среднесписочная).
Во многих формулах неизменно фигурирует Ссг — среднегодовая стоимость оборотных средств. Как её рассчитать? Существует очень простая формула: Ссг = Сп + Свв*ЧМ/12 — Сл*(12-М)/12.
Разберём, что означает каждая конкретная величина. «Сп» — это первоначальная стоимость оборотных средств, «Свв» — стоимость введённых средств, «ЧМ» — число месяцев функционирования введённых основных средств в течение года, «Сл» — ликвидационная стоимость. Можно также воспользоваться упрощённой формулой без учёта месяца ввода основных средств: Ссг=(Снг-Скг)/2. Здесь Снг — не Содружество независимых государств, а стоимость основных средств на начало года, а скг — соответственно, на конец года.
Также нам пригодится расчёт годовой суммы амортизации. Она рассчитывается по формуле: A=Сперв*Наморт/100. Норму амортизации также можно рассчитать по двум формулам: Наморт = (Пст — Лст) : (Ап · Пст), где Пст — первоначальная стоимость основных средств, Лст — ликвидационная стоимость, Ап — амортизационный период. Другая формула вычисляется с помощью срока службы объекта основных средств: Наморт = (1/Т)*100%.
Ещё рассмотрим формулы, которые пригодятся нам для решения задач по экономике труда. Формула для определения численности трудоспособного населения на конец какого либо периода (возьмём, к примеру, год) выглядит так: Чконец = Чначало + Ч1 -Ч2 — Ч3.
Здесь Чначало — численность трудящихся на начало года; Ч1 — число людей, вступивших в трудоспособный возраст; Ч2 — количество населения, умершего за период; Ч3 — численность выбывшего из трудоспособного возраста населения. Существует также формула годовой выработки работника: Вгод.раб.= Вчас.раб.*t*T*Ув.раб. , где Вчас.раб.
— выработка работника в час (денежная ед./чел-час); t — продолжительность рабочего дня (в часах); T — число дней в рабочем году; Ув.раб. — удельный вес рабочих в общей численности работающих.
Примеры задач
Рассмотрим задачи по экономике предприятия с решениями. Итак, задача номер 1: Определить среднегодовую стоимость основных средств с помощью предоставленных данных. Данные для решения:
Стоимость на начало года: 15 000 тыс. рублей.
Стоимость введённых ОС: март — 200 тыс. рублей.
июнь — 150 тыс. рублей.
август — 250 тыс. рублей.
Стоимость выбывших ОС: февраль — 100 тыс. рублей.
октябрь — 300 тыс. рублей.
Решение: формулы по экономике для решения задач нам здесь пригодились. Рассчитываем Ссг: (Снг-Скг)/2. Снг= 15 000 тыс. рублей; Скг= 15 000 + 200 + 150 + 250 — 100 — 300 = 15 200 тыс. рублей.
Тогда Ссг = (15000+15200)/2= 15 100 тыс. рублей. Однако мы получили не очень точный результат, так как ввод-вывод ОС был в течение года неравномерным. Попробуем расчитать Ссг по первой формуле: Ссг=Сп + Свв*ЧМ/12 — Сл*(12-М)/12 = 15 000 + (200*9/12 + 150*6/12 + 250*4/12) — (100*10/12 + 300*2/12) = 15 175 тыс. рублей.
Перейдём к другому заданию. Ниже представлена задача с решением по экономике предприятия, и она посвящена расчёту амортизации.
Задача №2:
Изначальная стоимость некоторых объектов на 1 января была равна 160 тыс. руб., а время фактической эксплуатации – 3 года.
Требуется рассчитать остаточную стоимость и коэффициент износа на эту же дату, при условии, что амортизация будет начисляться линейным способом. Срок службы объектов основных средств считать равным 10 годам.
Коэффициент износа — сумма амортизации за всё время (то есть 3 года). Итак, рассчитаем амортизацию линейным способом: А=Сперв*Наморт/100. Находим норму амортизации: Наморт= (1/Т)*100% = (1/10)*100% = 10%. Тогда А=160*10/100 = 16 тыс. рублей. Так как считаем сумму амортизации за каждый год одинаковой, то коэффициент износа за три года равен: И=3*16= 48 тыс. рублей.
Экономика труда: задачи с решениями
Перейдём к другому разделу. Мы уже рассмотрели задачи по экономике предприятия, с решениями которых вы могли ознакомиться выше. А теперь пришла пора для труда. И первая задача с решением по экономике, которую мы разберём, будет касаться численности трудоспособного населения.
Вычислить численность трудоспособного населения на конец года, если за текущий год имеются данные:
- число населения трудоспособного возраста в начале года – 60 млн. чел.;
- численность погибших людей в трудоспособном возрасте – 0,25 млн. чел.;
- количество молодых людей, достигших в текущем году трудоспособного возраста – 2,5 млн. чел.;
- численность лиц, ушедших на пенсию в текущем году – 1,5 млн. чел.
Решение. Итак, применим формулу, которую мы описали выше — Чконец = Чначало + Ч1 -Ч2 — Ч3 = 60 + 2,5 — 0,25 — 1,5 = 60,75 млн. человек.
В общем-то это вся задача с решением по экономике труда. Теперь разберём задачу с годовой выработкой.
Задача №2: Определить годовую выработку работника.
| Показатель | Базисный период | Отчётный период |
| Валовая продукция, тыс. ден. един. | 3800 | 3890 |
| Численность работающих, чел. | 580 | 582 |
| Удельный вес рабочих в численности работающих | 82,4 | 82,0 |
| Количество отработанных тысяч чел-дней | 117 | 114,6 |
| Количество отработанных тысяч чел-часов | 908,6 | 882,4 |
Выше мы обсуждали формулу для решения этой задачи. Теперь пора её применить: Вгод.раб.= Вчас.раб.*t*T*Ув.раб.
Найдём по порядку все величины. Выработка рабочего за час равна отношению выпущенной валовой продукции к количеству отработанных человеко-часов, т.е. Вчас.раб. = 3800/908,6 = 4,2. Чтобы узнать среднее время рабочего дня, нам нужно разделить количество отработанных человеко-часов на число человеко-дней.
Тогда t = 908,6/117=7,8 часов. Теперь осталось найти коэффициент Т, который означает продолжительность рабочего года и вычисляется как отношение отработанных тысяч чел-дней к числу рабочих. Чтобы узнать количество «трудяг», нам необходимо умножить их удельный вес на общую численность персонала. После этого нетрудно записать формулу: Т = 117*1000/(580*0,824) = 244,8 дня.
Сейчас нам просто нужно подставить все значения в формулу. Получаем: Вгод.раб.= 4,2*7,8*244,8*0,824 = 6608,2 ден.един./чел.

Что ещё?
Многие зададутся вопросом: разве это всё многообразие экономических задач? Вот так вот скучно? На самом деле нет. Просто в большинстве случаев затруднения вызывают именно эти разделы экономической науки: экономика производства, решение задач по которой мы рассмотрели в начале, а также экономика труда.
Существует очень много других отраслей, однако как таковых сложных формул там нет, и очень часто можно даже логически применить тот или иной математический закон. Однако каждому будет полезно прочитать задачи по экономике с решением. Для студентов это особенно актуально, так как возможность посмотреть решение существенно облегчает понимание задачи и лучше доносит до человека её суть.
Что ещё можно почитать или порешать на досуге для лучшего понимания темы? Рекомендуем порешать задачи из сборника Ревенко Н. Ф. по экономике предприятия. А также неплохо было бы прочесть более специализированные книги на какую-либо конкретную тематику.

Заключение
Экономика — очень древняя и важная наука, и на протяжении многих веков она шла нога в ногу с математикой. Её законы позволяли предугадывать кризисы, изменение обстановки в стране и тому подобное. Если человек обладает экономическим знанием, он вряд ли пропадёт в период кризиса или локальной финансовой катастрофы.
Если совершенствовать свои знания, они наверняка принесут пользу в жизни и помогут в повышении финансового благополучия. Конечно, мы рассмотрели лишь примеры решения задач по экономике, и это не значит, что реальные задачи будут выглядеть именно так. В жизни всё, как правило, сложнее и запутаннее. Поэтому, если вы хотите всегда быть на высоте, то задача с решением по экономике вам поможет не так сильно. Гораздо важнее проявить смекалку.
Источник: fb.ru
Как решать экономические задачи — алгоритм решения экономических задач егэ по математике профильный уровень

Математика
Автор Ольга Андрющенко На чтение 12 мин Просмотров 40.3к. Опубликовано 7 февраля, 2019
Для решения таких задач необходимо понимать алгоритм решения экономических задач
За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.
Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.
Можно выделить несколько блоков заданий:
1. Вклады и кредиты
2. Акции и другие ценные бумаги
3. Методы оптимальных решений
Рассмотрим каждый из вышеперечисленных блоков.
Вклады и кредиты
Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.
Формула выглядит следующим образом:
где FV – будущая сумма.
PV – текущая сумма.
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента.
Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:
,
FV – будущая сумма
PV – текущая сумма
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента
m – количество начислений в год (например, m=4, если начисления ежеквартальные).
Давайте отработаем эту формулу на подготовительной задаче.
Задача 1
Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?
Решение:
Рассчитаем по формуле сложного процента сумму через год:
![]()
Теперь сумму через 2 года:
![]()
Теперь сумму через 3 года:
![]()
Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения /неравенства.
Задача 2
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.
Решение:
Пусть искомая сумма составит a млн рублей.
Составим таблицу, чтобы упорядочить данные и построить математическую модель.

По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
14,641 + 2,31a ≥ 28
a ≥
Наименьшее целое число, при котором знак неравенства выполняется, это число 6.
Значит, искомая сумма — 6 млн рублей.
Ответ: 6 млн рублей.
Акции и другие ценные бумаги
Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.
Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.
Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.
Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.
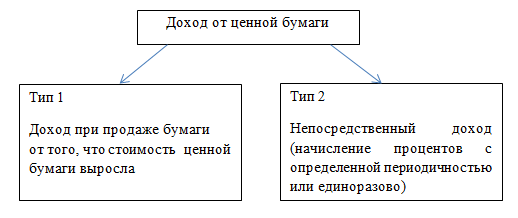
Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.
Задача 3.
Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.
К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:
Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.
Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.
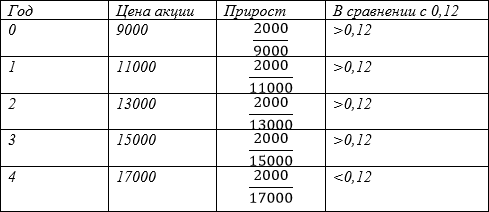
Либо можем составить уравнение, которое объединит все строчки нашей таблицы:

По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.
Методы оптимальных решений
Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.
Основные типы заданий в этом блоке:
1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;
2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);
3. Транспортная задача.
Разберём несколько задач с основными методами решения.
Задача.
У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.
Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?
Решение:
Имеем 2 поля с различными характеристиками.
В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.
Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:
10·500· 9000= 45000000 рублей
Ситуация с первым полем не так очевидна.
Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).
Поэтому необходимо сравнить соотношения этих величин:
Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.
Доход с первого поля:
10 · 500 ·7000 = 35000000 рублей
Суммарный доход составит:
35000000 рублей + 45000000 рублей = 80000000 рублей
Ответ: 80000000 рублей
Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.
Задача.
На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.
Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?
Решение:
Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.
Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.
Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.
На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.
Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:
![]()
Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:
1. Найти производную функции;
2. Приравнять производную к 0, получить точки, подозрительные на экстремум;
3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.
Проведём такую последовательность действий с нашей производственной функцией.

-
 Приведём к общему знаменателю.
Приведём к общему знаменателю.  Приравняем числитель к 0. Возведём в квадрат. Получили единственную точку экстремума.
Приравняем числитель к 0. Возведём в квадрат. Получили единственную точку экстремума. - Проверим, является ли она точкой максимума.
 Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.
Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.  Ответ: 600 кг
Ответ: 600 кг
Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.
Самое главное – внимательно прочитать и понять условие.
Примеры решения задач
Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.
![]()
Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму
Воспользуемся этой формулой, считаяS0= 100 000, r = 11 , m = 30 (так как в ноябре 30 дней).
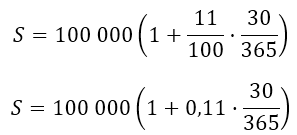
Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.
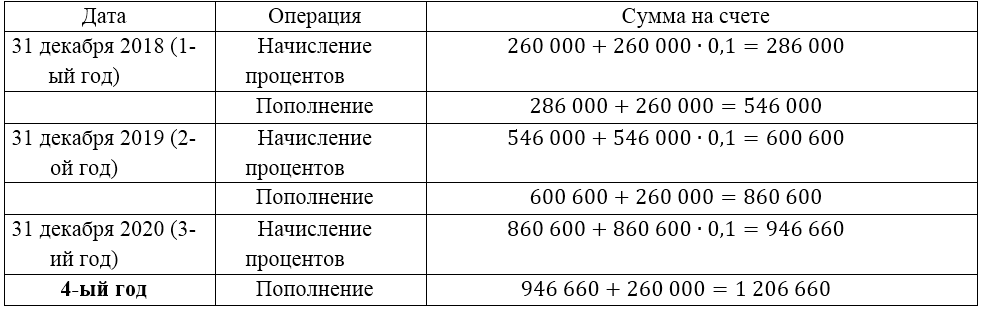
Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?
Решение:
Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.
Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».
Решение:
![]()
Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на
умножается на коэффициент 1,1.
Тогда по вкладу «А» после первого года сумма станет равна ;
после второго года: 1,21S;
после третьего года: 1,331S.
По вкладу «Б» после первого года сумма станет равна1,11S;
после второго года 1,2321S.
Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна
, где r— натуральное число,
коэффициент повышения в третий год.
По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:
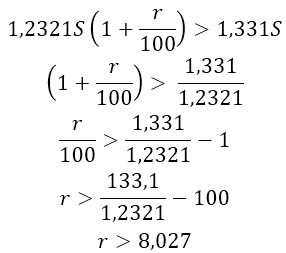
Так как r— натуральное число, то наименьший процент равен 9%.
Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%.
В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?
Решение.
Во второй год цена ценной бумаги составит: (7+2) тысячи рублей
В третий год (7+2)+2= 7+2∙2 тысячи рублей
В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей
![]()
.
Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.
![]()
10% от цены бумаги на
Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.
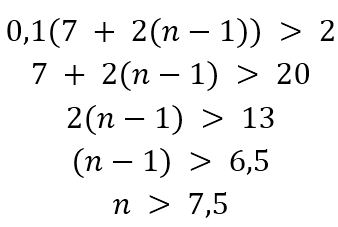
Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.
Задача 5.
Пенсионный фонд владеет ценными бумагами, которые стоят t 2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?
Решение:

Ряд активности металлов
Акции компании — дивиденды, виды, права
Щелочные металлы список и свойства
Город федерального значения Москва — история и факты
Как найти процент от числа
Источник: novstudent.ru

 Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.
Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.