Использование математической оптимизации (далее МО ) предоставляет компаниям и медиа значительные преимущества при развертывании рекламных и маркетинговых кампаний. МО предоставляет организациям возможность использовать постоянно растущие объемы данных для принятия миллионов автоматизированных решений, максимизируя при этом окупаемость инвестиций, одновременно расширяя и улучшая отношения с клиентами, предоставляя нужным людям нужные сообщения в нужное время.
Решаемые задачи
— Максимизация эффективности стратегий автоматического назначения ставок для ресурсов (Google Ads, Yahoo Ads, Yandex.Direct др.)
— Максимизация ROI планируемых маркетинговых / рекламных акций;
— Максимизация эффективности политической агитации;
— Позиционирование и вывод нового продукта на рынок;
— Повышение эффективности системы взаимодействия с клиентами, разработка оптимальных расписаний взаимодействия с пользователями;
— Расширенный анализ поведения пользователей;
Оптимизация бизнес-процессов
— Разработка комплексных маркетинговых акций;
— Разработка стратегии Кросс-продаж;
Проекты
Преимущества использования Математической оптимизации
Решаемые задачи
Проекты
Преимущества использования Математической оптимизации
Решаемые задачи
Проекты
Преимущества использования Математической оптимизации
Решаемые задачи
Решаемые задачи
- Сокращение сроков строительства за счет совмещения работ на отдельных участках;
- Максимизация загрузки имеющихся ресурсов и оборудования;
- Экономическое обоснование использования технологических новаций;
- Минимизация себестоимости работ.
- Расчёт оптимального уровня цены продажи м.кв. помещений, с учетом сезонной и ценовой эластичности спроса;
- Разработка комплексного маркетингового плана. Бюджетирование;
- Разработка и обоснование плана ежемесячных продаж;
- Разработка плана размещения свободных оборотных средств в финансовые инструменты;
- Максимизация прибыли продаж.
Проекты

ПОДБЕРЕМ ДЛЯ ВАС РЕШЕНИЕ
Оставьте контактные данные и мы свяжемся с вами
5 УСЛОВИЙ, ПРИ НАЛИЧИИ КОТОРЫХ ВНЕДРЕНИЕ МАТЕМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ЭКОНОМИЧЕСКИ ЦЕЛЕСООБРАЗНО
Стоимость оптимизируемого бизнес-процесса
> 30 000$ в год
Стейкхолдеры:
Собственники, менеджеры
высшего и среднего звена
Повторяемость оптимизируемого бизнес-процесса
Стейкхолдеры:
Собственники, менеджеры
высшего и среднего звена
Сложность принятия решения, в т.ч. ввиду наличия больших данных
Стейкхолдеры:
Собственники, менеджеры
высшего и среднего звена
Противоречивость последствий принимаемых решений
Стейкхолдеры:
Собственники, менеджеры
Оптимизация бизнес-процессов. С чего начинать? Главные этапы автоматизации //16+
высшего и среднего звена
Высокая конкурентная среда
Стейкхолдеры:
Собственники, менеджеры
высшего и среднего звена
Что мы предлагаем?
Разработка моделей математической оптимизации
Внедрение готовых отраслевых решений
Сопровождение моделей оптимизации
Продажа ПО для математической оптимизации: AMPL и Solvers
Часто задаваемые вопросы
Математическая оптимизация (далее МО), также известна как экономико-математическое моделирование, и/или математическое программирование (берет свой отсчет с работ советского академика (1939 год), лауреата Нобелевской премии (1975) Л. В. Канторовича) – это представление свойств реального объекта или процесса в виде математических формул, уравнений, неравенств, с целью определения max/min-мального возможного значения результатов их деятельности в условиях действующих ограничений. МО – это процесс выбора наилучшего значения (по выбранному критерию) из некоторого набора доступных альтернатив. Необходимость решения задач математической оптимизации возникает всякий раз, когда имеются альтернативные варианты использования имеющихся ресурсов.
Например: представим, что у нас имеются средства, которые мы хотим направить на рекламу. В этом случае нам понадобится проанализировать имеющиеся виды рекламных носителей (печатные, цифровые, радио) их условия/требования к размещаемым материалам, структуру и численный состав целевой аудитории, показатель конверсий и т.д. После чего мы сможем определить наилучший для нас вариант (с точки зрения критерия эффективности) вложения наших средств.
Таким образом, вышеописанный процесс:
– расчет имеющихся вариантов;
– сравнение между собой полученных результатов;
– выбор наилучшего результата
и есть задача математической оптимизации (в самом общем ее виде).
Проблемы оптимизации возникают во всех точных дисциплинах, от информатики и инженерии до исследования операций, экономики и медицины.
Более 80% компаний из списка Fortune 500 используют математическую оптимизацию в различных сферах своей деятельности, получая от этого максимально эффективные бизнес-решения, реализация которых позволяет зарабатывать и экономить десятки и сотни миллионов долларов.
— Превращает бизнес-задачу в математическую модель, а затем находит для нее наилучшее решение, представляя подробный план действий по его достижению.
— Используется в качестве средств стратегического планирования, что бы предвидеть будущее, исследовать альтернативы, разработать несколько планов на случай различного развития событий.
— Предоставляет бизнесу четкий ответ на вопрос: «Что нужно сделать для увеличения эффективности/прибыльности ?»
— Существенно преобразовала такие отрасли как: авиация, логистика, финансы, энергетика, телекоммуникации, предоставив компаниям возможность решать их сложнейшие задачи и принимать оптимальные решения, максимально повышающие их операционную эффективность.
Приложения математической оптимизации состоят из двух основных компонентов: математической модели и решателя.
Математическая модель представляет собой подробное математическое описание бизнес-задачи, которая включает в себя корпоративные бизнес-правила, бизнес-цели и бизнес-логику принимаемых решений. Такой подход позволяет относительно быстро и без существенных затрат исследовать свойства и прогнозировать поведение и состояние исследуемого направления в интересующих нас условиях.
Математическая оптимизация имеет в своем распоряжении большой набор инструментов и практик для описания финансово-экономических характеристик рассматриваемых объектов (процессов) и их отношений с внешней средой и внутренними элементами.
Решатель – это набор алгоритмов искусственного интеллекта, который решает математическую модель. Для большинства пользователей решатель работает как «черный ящик». Пользователи используют его результаты, но мало понимают его внутреннюю работу. Да это по сути и не нужно. Внутри «черного ящика» находится коллекция самых сложных и современных (результат более чем 70 летнего труда) математических алгоритмов.
Архитектура приложений математической оптимизации имеет гибкую структуру и может быть реализована в одном из следующих вариантов:
Источник: www.solverytic.com
Какие существуют методы оптимизации? Методы оптимизации управленческих решений
Наиболее приемлемый вариант решения, которое принимается на управленческом уровне относительно любого вопроса, принято считать оптимальным, а сам процесс его поиска – оптимизацией.
Взаимозависимость и сложность организационных, социально-экономических, технических и иных аспектов управления производством в настоящее время сводится к принятию управленческого решения, которое затрагивает большое количество разного рода факторов, тесно переплетающихся друг с другом, ввиду чего становится невозможным произвести анализ каждого отдельно с использованием традиционных аналитических методов.
Большинство факторов выступают определяющими в процессе принятия решения, и они (по своей сути) не поддаются какой-либо количественной характеристике. Также существуют и такие, которые практически неизменны. В связи с этим возникла необходимость в разработке особых методов, способных обеспечить выбор важных управленческих решений в рамках сложных организационных, экономических, технических задач (экспертные оценки, исследование операций и методы оптимизации и др.).
Методы, направленные на исследование операций, применяются в целях поиска оптимальных решений в таких областях управления, как организация процессов производства и перевозок, планирование крупномасштабного производства, материальное и техническое снабжение.
Методы оптимизации решений заключаются в исследовании посредством сравнения числовых оценок ряда факторов, анализ которых традиционными методами осуществить нельзя. Оптимальное решение – наилучшее среди возможных вариантов относительно экономической системы, а наиболее приемлемое в отношении отдельно взятых элементов системы – субоптимальное.
Сущность методов исследования операций
Как уже было упомянуто ранее, они формируют методы оптимизации управленческих решений. Их основа – математические (детерминированные), вероятностные модели, представляющие исследуемый процесс, вид деятельности или систему. Данного рода модели представляют количественную характеристику соответствующей проблемы. Они служат базой для принятия важного управленческого решения в процессе поиска оптимально приемлемого варианта.
Перечень вопросов, которые играют существенную роль для непосредственных руководителей производства и которые разрешаются в ходе использования рассматриваемых методов:
- степень обоснованности выбранных вариантов решений;
- насколько они лучше альтернативных;
- степень учета определяющих факторов;
- каков критерий оптимальности выбранных решений.
Данные методы оптимизации решений (управленческих) нацелены на поиск оптимальных решений для как можно большего количества фирм, компаний либо их подразделений. Они основаны на существующих достижениях статистических, математических и экономических дисциплин (теории игр, массового обслуживания, графиков, оптимального программирования, математической статистики).

Методы экспертных оценок
Данные методы оптимизации управленческих решений применяются, когда задача частично либо полностью не подвержена формализации, а также ее решение не может быть найдено посредством математических методов.
Экспертиза – это исследование сложных особых вопросов на этапе выработки определенного управленческого решения соответствующими лицами, которые владеют специальным багажом знаний и внушительным опытом, для получения выводов, рекомендаций, мнений, оценок. В процессе экспертного исследования применяются новейшие достижения и науки, и техники в рамках специализации эксперта.
Рассматриваемые методы оптимизации ряда управленческих решений (экспертных оценок) эффективны в решении нижеперечисленных управленческих задач в сфере производства:
- Изучение сложных процессов, явлений, ситуаций, систем, которые характеризуются неформализованными, качественными характеристиками.
- Ранжирование и определение согласно заданному критерию существенных факторов, выступающих определяющими относительно функционирования и развития производственной системы.
- Рассматриваемые методы оптимизации особо эффективны в области прогнозирования тенденций развития системы производства, а также ее взаимодействия с внешней средой.
- Повышение надежности экспертной оценки преимущественно целевых функций, которые имеют количественный и качественный характер, посредством усреднения мнений квалифицированных специалистов.
И это лишь некоторые методы оптимизации ряда управленческих решений (экспертной оценки).

Классификация рассматриваемых методов
Методы решения задач оптимизации, исходя из числа параметров, можно подразделить на:
- Методы оптимизации одномерной.
- Методы оптимизации многомерной.
Их еще называют «численные методы оптимизации». Если быть точным, это алгоритмы ее поиска.
В рамках применения производных методы бывают:
- прямые методы оптимизации (нулевого порядка);
- градиентные методы (1-го порядка);
- методы 2-го порядка и др.
Большая часть методов многомерной оптимизации приближена к задаче второй группы методов (одномерной оптимизации).

Методы одномерной оптимизации
Любые численные методы оптимизации основаны на приближенном либо точном вычислении таких ее характеристик, как значения целевой функции и функций, которые задают допустимое множество, их производные. Так, для каждой отдельной задачи вопрос тносительно выбора характеристик для вычисления может быть решен в зависимости от существующих свойств рассматриваемой функции, имеющихся возможностей и ограничений в хранении и обработке информации.
Существуют следующие методы решения задач оптимизации (одномерной):
- метод Фибоначчи;
- дихотомии;
- золотого сечения;
- удвоения шага.

Метод Фибоначчи
Для начала необходимо установить координаты т. x на промежутке [a; b] в качестве числа, равного отношению разницы (x — a) к разнице (b — a). Следовательно, a имеет относительно промежутка [a; b] координату 0, а b – 1, средняя точка – ½.
Если допустить, что F0 и F1 между собой равны и принимают значение 1, F2 будет равно 2, F3 – 3, …, то Fn = Fn-1 + Fn-2. Итак, Fn – числа Фибоначчи, а поиск Фибоначчи – это оптимальная стратегия так называемого последовательного поиска максимума ввиду того, что она довольно тесно связана с ними.
В рамках оптимальной стратегии принято выбирать xn – 1 = Fn–2 : Fn, xn = Fn–1 : Fn. При любом из двух интервалов ([0; xn] либо [xn–1; 1]), каждый из которых может выступать в качестве суженного интервала неопределенности, точка (унаследованная) относительно нового интервала будет иметь либо координаты [Fn–3: Fn–1], либо [Fn–2 : Fn-1]. Далее, в качестве xn – 2 принимается точка, которая имеет относительно нового промежутка одну из представленных координат. Если использовать F(xn — 2), значение функции, которое унаследовано от прежнего промежутка, становится возможным сокращение интервала неопределенности и передача в наследство одного значения функции.
На финишном шаге получится прейти к такому интервалу неопределенности, как [a; b], при этом средняя точка унаследована от предыдущего шага. В качестве x1 устанавливается точка, которая имеет относительную координату ½+ε, а окончательный интервал неопределенности будет [0, ½+ε] или [½, 1] по отношению к [a; b].
На 1-м шаге длина данного интервала сократилась до Fn–1 : Fn (с единицы). На финишных шагах сокращение длин соответствующих интервалов представляется числами Fn–2 : Fn–1, Fn–3 : Fn–2, …, F2 : F3, F1 : F2 (1 + 2ε). Итак, длина такого интервала, как окончательный вариант примет значение (1 + 2ε) : Fn.
Если пренебречь ε, то асимптотически 1 : Fn будет равно rn, при этом n→∞, а r = (√5 – 1) : 2, что приблизительно равно 0,6180.
Стоит отметить, что асимптотически для значительных n каждый последующий шаг поиска Фибоначчи существенно сужает рассматриваемый интервал с вышеуказанном коэффициентом. Данный результат требуется сравнить с 0,5 (коэффициент сужения интервала неопределенности в рамках метода бисекции для поиска нуля функции).
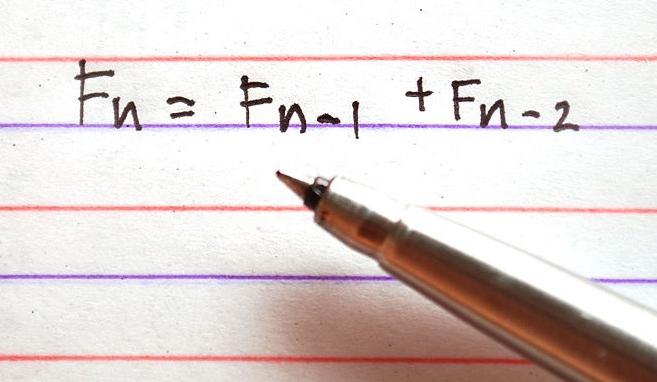
Метод дихотомии
Если представить некую целевую функцию, то для начала потребуется найти ее экстремум на промежутке (a; b). Для этого ось абсцисс делится на четыре эквивалентные части, затем необходимо определить значение рассматриваемой функции в 5 точках. Далее выбирается минимум среди них. Экстремум функции должен лежать в пределах промежутка (a’; b’), который прилегает к точке минимума.
Границы поиска сужаются в 2 раза. А если минимум расположен в т. a либо b, то он сужается во все четыре раза. Новый интервал также разделяется на четыре равных отрезка. В связи с тем, что значения данной функции в трех точках были определены на предыдущем этапе, далее требуется вычислить целевую функцию в двух точках.
Метод золотого сечения
Для существенных значений n координаты таких точек, как xn и xn–1 приближены к 1 – r, равное 0,3820, а r ≈ 0,6180. Толчок с данных значений весьма близок к искомой оптимальной стратегии.
Если предположить, что F(0,3820) > F(0,6180), то тогда очерчивается интервал [0;0,6180]. Однако ввиду того, что 0,6180 * 0,6180 ≈ 0,3820 ≈ xn-1, то в данной точке F уже известна. Следовательно, на каждом этапе, начиная со 2-го, необходимо только одно вычисление целевой функции, при этом каждый шаг сокращает длину рассматриваемого интервала с коэффициентом 0,6180.
В отличие от поиска Фибоначчи, в данном методе не требуется фиксация числа n еще до начала поиска.
«Золотое сечение» участка (a; b) – сечение, при котором отношение его r длины к более крупной части (a; c) идентично отношению большей части r к меньшей, то есть (a; с) к (c; b). Нетрудно догадаться, что r определяется по вышерассмотренной формуле. Следовательно, при существенных n метод Фибоначчи переходит в данный.
Метод удвоения шага
Суть – поиск направления убывания целевой функции, движение в данном направлении в случае удачного поиска с постепенно возрастающим шагом.
Сначала определяем начальную координату M0 функции F(M), минимальное значение шага h0, направление поиска. Затем определяем функцию в т. M0. Далее совершаем шаг и находим значение данной функции в данной точке.
В случае если функция меньше значения, которое было на предыдущем шаге, следует произвести следующий шаг в том же направлении, предварительно увеличив его в 2 раза. При ее значении, которое больше предыдущего, потребуется поменять направление поиска, а затем начать двигаться в выбранном направлении с шагом h0. Представленный алгоритм можно модифицировать.
Методы многомерной оптимизации
Вышеупомянутый метод нулевого порядка не берет в расчет производные минимизированной функции, ввиду чего их использование может быть эффективно в случае возникновения каких-либо трудностей с вычислением производных.
Группу методов 1-го порядка еще называют градиентными, потому что для установления направления поиска применяют градиент данной функции – вектор, составляющими которого выступают частные производные минимизированной функции по соответствующим оптимизированным параметрам.
В группе методов 2-го порядка применяются 2 производные (их использование достаточно ограничено ввиду наличия трудностей в их вычислении).
Перечень методов безусловной оптимизации
При использовании многомерного поиска без применения производных методы безусловной оптимизации следующие:
- Хука и Дживса (осуществление 2 видов поиска – по образцу и исследующий);
- минимизации по правильному симплексу (поиск точки минимума соответствующей функции посредством сравнения на каждой отдельной итерации ее значений в вершинах симплекса);
- циклического координатного спуска (использование в качестве ориентиров поиска координатных векторов);
- Розенброка (основан на применении одномерной минимизации);
- минимизации по деформированному симплексу (модификация метода минимизации по правильному симплексу: добавление процедуры сжатия, растяжения).
В ситуации использования производных в процессе многомерного поиска выделяют метод наискорейшего спуска (наиболее фундаментальная процедура минимизации дифференцируемой функции с несколькими переменными).
Также выделяют еще такие методы, которые используют сопряженные направления (Метод Дэвидона-Флетчера-Пауэлла). Его суть – преставление направлений поиска как Dj*grad(f(y)).
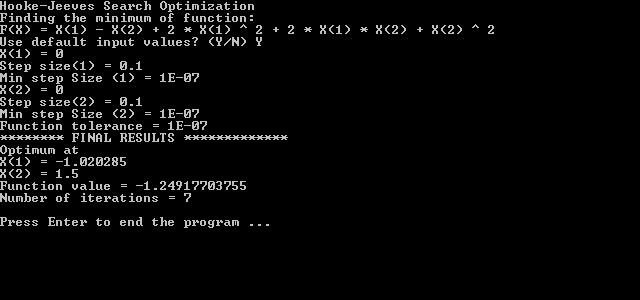
Классификация математических методов оптимизации
Условно, исходя из размерности функций (целевых), они бывают:
- с 1 переменной;
- многомерные.
В зависимости от функции (линейная или нелинейная) существует большое количество математических методов, направленных на поиск экстремума для решения поставленной задачи.
По критерию применения производных математические методы оптимизации подразделяются на:
- методы вычисления 1 производной целевой функции;
- многомерные (1-я производная–векторная величина–градиент).
Исходя из эффективности вычисления, существуют:
- методы быстрого вычисления экстремума;
- упрощенного вычисления.
Это условная классификация рассматриваемых методов.
Оптимизация бизнес-процессов
Методы здесь могут использоваться различные, в зависимости от решаемых проблем. Принято выделять следующие методы оптимизации процессов бизнеса:
- исключения (уменьшение уровней существующего процесса, ликвидация причин помех и входного контроля, сокращение транспортных путей);
- упрощения (облегченное прохождение заказа, снижение комплексности продуктовой структуры, распределение работ);
- стандартизации (использование специальных программ, методов, технологий и т. д.);
- ускорения (параллельный инжиниринг, стимуляция, оперативное проектирование опытных образцов, автоматизация);
- изменение (перемены в области сырья, технологий, методов работ, кадрового расположения, рабочих систем, объема заказа, порядка обработки);
- обеспечения взаимодействия (в отношении организационных единиц, персонала, рабочей системы);
- выделения и включения (относительно необходимых процессов, комплектующих).
Налоговая оптимизация: методы
Российское законодательство предоставляет налогоплательщику весьма богатые возможности сокращения размеров налогов, ввиду чего принято выделять такие способы, направленные на их минимизацию, как общие (классические) и специальные.
Общие методы налоговой оптимизации следующие:
- проработка учетной политики компании с максимально возможным применением предоставленных российским законодательством возможностей (порядок списания МБП, выбор метода расчета выручки от реализации товара и др.);
- оптимизация посредством договора (заключение льготированных сделок, четкое и грамотное использование формулировок и т. п.);
- применение разного рода льгот, налоговых освобождений.

Вторую группу методов также могут использовать все фирмы, однако они все же имеют достаточно узкую область применения. Специальные методы оптимизации налогов следующие:
- замены отношений (операция, которая предусматривает обременительное налогообложение, замещается другой, которая позволяет достичь аналогичную цель, но при этом использовать льготный порядок налогового обложения).
- разделения отношений (замена лишь части хозяйственной операции);
- отсрочки налогового платежа (перенесение момента появления объекта налогообложения на другой календарный период);
- прямого сокращения объекта налогового обложения (избавление от многих налогооблагаемых операций либо имущества без оказания негативного влияния на основную хозяйственную деятельность компании).
Источник: www.syl.ru
Введение в математическую оптимизацию на примере компании Recruit. Часть 1

Прим. переводчика : Ранее на хабре не было переводов статей с японского языка. Мы решили исправить это досадное упущение и начать переводить их ещё и с этого языка. Данный материал будет пробой пера.
Эта серия статей о том, что такое математическая оптимизация и как она может быть применена в бизнесе через представление примеров применения в компании Recruit. В первой статье представлен обзор математической оптимизации, четыре примера применения в Recruit, процедура применения к реальным случаям, отличия от машинного обучения и как использовать её иначе.
Другие части доступны здесь:
- Введение в математическую оптимизацию на примере компании Recruit. Часть 2
- Введение в математическую оптимизацию на примере компании Recruit. Часть 3
В последние годы использование данных в бизнесе стало обычным делом для многих компаний. Многие читатели слышали об историях успеха, связанных, в частности, с использованием машинного обучения. С другой стороны, мало кто знает о реальности математической оптимизации — ещё одной техники использования данных, хотя она и достигает немалых результатов в различных областях.
