1 Челябинский институт (филиал) Российский государственный экономический университет им. Г.В. Плеханова
Применение моделирования экономических процессов обусловлено целью воссоздания многочисленных связей, существующих в экономике, и установления степени влияния внутренних и внешних факторов на результаты производственно-хозяйственной деятельности, а также решения конкретных экономических задач. Данная статья является иллюстрацией навыка формулирования экономико-математических задач, их решения и далее проведения анализа на фактическом материале.
Использование экономико-математической модели для текущего планирования развития производства и планирования на перспективу позволяет определить его основные параметры. Разрабатываемая модель применима при анализе образовавшейся структуры производства. С ее помощью возможно выявление наиболее целесообразных путей расходования ресурсов и наращивания объемов выпускаемой продукции при опоре на достоверные данные. Разработанная экономико-математическая модель оптимизации для организаций обосновывает изменения в структуре производства, что направлено на получение максимальной прибыли с полным использованием ресурсного потенциала.
Математические модели. Стохастические модели

оптимизация
экономико-математическое моделирование
прогнозирование производства продукции
1. Электронный учебник по статистике StatSoft. [Электронный ресурс]. – Электрон. дан. – Режим доступа: www.StatSoft.ru/ home/ textbook.
2. Жуковская В. М., Мучник И. Б. Факторный анализ в социально- экономических исследованиях. – М.: Статистика, 1976. – С. 37–78
3. Иберла К. Факторный анализ: пер. с нем. – М.: Статистика, 1980. – С. 85–110.
4. Лоули Д., Максвелл А. Факторный анализ как статистический метод: пер. с англ. – М.: Мир, 1967. – С. 72–130.
5. Окунь Я. Факторный анализ: пер. с польск. – М.: Статистика, 1974. – С. 42–75.
6. Бююль А., Цефель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей: пер. с нем. – СПб.: ДиаСофтЮП. 2001. – С. 40–55.
7. Маркин Б.Г. Анализ качественных признаков и структур. – М.: Статистика, 1980. – С. 124–155.
8. Колемаев В.А., Калинина В.Н. Теория вероятностен и математическая статистика: учебник. – М.: ЮНИТИ-ДАНА, 2003. – С. 74–85.
9. Сошникова Л.А., Тамашевич В., Уебе Г., Шефер М. Многомерный статистический анализ в экономике: учеб. пособие. – М.: ЮНИТИ-ДАНА. 1999. – С. 174–178.
10. Попов, Э.В. Статистические и динамические экспертные системы / Э.В. Попов, И.Б. Фоминых, Е.Б. Кисель, М.Д.
Шапот. – М.Финансы и статистика, 1996. – С. 36–57.
Составление прогнозов развития производства продукции представляет собой актуальную задачу на местном, региональном, федеральном уровнях, для отдельных организаций. В силу ряда микро- и макроэкономических причин на современном этапе экономических реформ сделать это довольно трудно. В настоящее время не существует общепризнанных методов, которые позволяют прогнозировать развитие производства продукции в организациях на перспективу с удовлетворительной достоверностью. Также необходимо отметить, что укрепление экономической свободы участников воспроизводственного процесса на уровне регионов обуславливает вероятностный образ экономических процессов, происходящих в различных отраслях, и заставляет применять сценарный подход и многовариантные альтернативные пути поиска решений.
Бизнес это математические модели
Для решения данной проблемы предлагается использовать методы экономико-математического моделирования и многомерного статистического анализа – один из главных инструментов прогрессирования хозяйственного механизма, структурного преобразования регионального рынка и прогнозирования динамики производства и реализации продукции. Изменения, происходящие в современной экономике, приводят к составлению новых и совершенствованию разработанных систем экономико-математического моделирования. Все это позволяет выявить скрытые резервы экономического роста организаций на уровне региона.
Разновидностью экономико-математических моделей является оптимизационная модель. Ее использование позволяет подвергнуть анализу динамику развития организаций региона и воспользоваться большими массивами реальной информации.
В данной статье предлагается построенная на ряде ограничений (что соответствует определенному использованию производственных ресурсов) модель оптимизации производства сельскохозяйственной продукции, которая позволит предприятию повысить рентабельность своего производства [1].
В настоящий момент финансово-экономическое состояние сельскохозяйственных организаций различных формообразований остается достаточно сложным. Отрицательное воздействие на финансово-экономическое состояние сельскохозяйственных организаций оказывают следующие факторы:
– увеличение физического и морального износа основных производственных фондов;
– снижение урожайности сельскохозяйственных культур как печальное следствие уменьшения минеральных удобрений из-за отсутствия денег;
– падение объемов производства сельскохозяйственной организации и сбыта ее различных видов продукции;
– низкие объемы инвестиций в инфраструктуру производственного и социального назначения;
– недостаточная обеспеченность специалистами и отсутствие квалификации задействованных производственных рабочих;
– снижение технической оснащенности сельхозтоваропроизводителей [9].
Итоговая цель создания модели заключается в формировании эффективных предпосылок интенсивного развития сельскохозяйственного производства и получения наибольшей прибыли, что является важным показателем эффективности финансово-экономической деятельности. Это обеспечивается рациональным использованием возможных производственных ресурсов и способствует повышению рентабельности хозяйственной деятельности сельскохозяйственных организаций в современных условиях. [8].
Решение разработанной экономико-математической модели проводится в несколько этапов (рисунок).
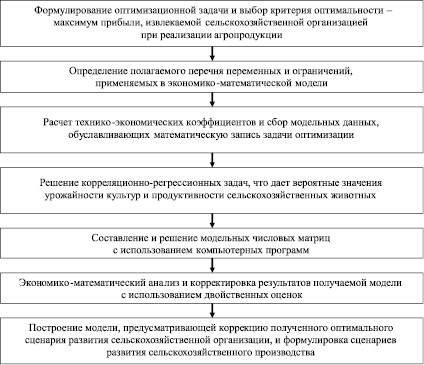
Этапы разработки экономико-математической модели по оптимизации производства продукции
Предполагается деление входной информации на следующие группы:
1. Производственные расходы (трудовые, на образование страхового фонда, на корма, на материальные затраты в расчете на единицу произведенной сельскохозяйственной продукции).
2. Результаты переменных (данные урожайности сельскохозяйственных культур и продуктивности животных – уровни выхода товарной и валовой продукции, кормовых единиц и протеина).
3. Земельные ресурсы, объемы в соответствии с производством, использованием и реализацией сельскохозяйственной продукции.
Разработанные модели оптимизации позволяют свести до возможного минимума недостаток ресурсов, имеющийся в сельскохозяйственных организациях, главным образом за счет рационального использования трудовых, земельных, финансовых, технических и других n-ресурсов, удобрений и кормов. Поставленная задача достигается через критерий оптимизации анализируемой системы [10].
Исследование модели на множества появляющихся в процессе решения других вариантов развития сельскохозяйственного производства позволяет изучить и обнаружить наилучший вариант в соответствии с согласованным критерием оптимизации. Отобранный критерий, согласно установленной задаче, отвечает требованию обеспечения выполнения обязательств по поставкам продукции в соответствии с договорами и в государственные фонды. Тем самым учитывается круг интересов и заказчика продукции, и ее производителей [3].
При построении оптимизационной модели необходимо учитывать следующие основные переменные: поголовье скота по видам, площади кормовых угодий, посевные площади сельскохозяйственных культур. Помимо основных, в модели включаются и вспомогательные переменные, которые отражают величины производства и реализации продаваемой продукции растениеводческой и животноводческой отраслей, оптимальную организацию рационов корма животных, объемы производства и расходования кормов [5].
В модель также вводятся ограничения:
– гарантированное производство основных видов товарной продукции для государственных фондов и обязательное выполнение в соответствии с договорами о поставках сельскохозяйственной продукции;
– величина земельных ресурсов, поголовья скота;
– производство и использование кормов;
– производство и реализация сельскохозяйственной продукции;
В рамках существующих границ региона исследования применяются изменения базовых параметров составленных моделей, которые в свою очередь опираются на фактические размеры отраслей растениеводства и животноводства.
Использование многофакторного анализа корреляционно-регрессионного типа для расчета порядка модельных коэффициентов осуществляется по нескольким производственным функциям с целью выбора наилучших прогнозируемых вероятных уровней показателей всходов сельскохозяйственных культур и продуктивности животных с экстраполяцией данных динамических рядов.
Рассчитывается предлагаемый оптимальный баланс в экономико-математических моделях производства и потребления кормов. Моделирование кормовой базы предполагает, что для каждого вида сельскохозяйственных животных корма должны быть агрегированы в соответствии с группой детализации отдельных видов кормов [4].
Составленные экономико-математические модели являются статически значимыми. Оптимизационную задачу структуры сельскохозяйственного производства для каждой организации региона можно представить следующим образом:
где Z – целевая функция, выраженная в максимизации прибыли; X – совокупность выручки от реализации сельскохозяйственной продукции; Y – совокупность производственных затрат на продукцию.
На основе составления модели решаемой задачи при экономико-математическом моделировании предполагается использование методов математической формализации условий и требований, предъявляемых к производству сельскохозяйственной продукции.
При решении задачи и выбора наилучшего варианта развития и размещения производства необходимо использовать систему ограничений сельскохозяйственной продукции, которая включает пределы снизу и сверху. Это позволит обеспечить достижение планируемых темпов прироста при правильной организации сельскохозяйственной продукции не только по количественным, но и качественным техническим и экономическим показателям [6].
Построение оптимизационной задачи включает следующие ограничения:
1. По использованию кормовых угодий и пашни:
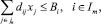
где j – порядковый номер переменной (j = 1, 2, …, n); i – порядковый номер ограничений (i = 1, 2, …, m); dij – затраты i-го n-ресурса на единицу измерения j-й отрасли; xj – аргумент, обозначающий размер j-й отрасли; Вi – ограничивающий размер угодий сельскохозяйственного назначения i-го вида; Jn – множество переменных в соответствии с сельскохозяйственными культурами и угодьями; Im – множество ограничений в соответствии с использованием пашни и кормовых угодий.
2. По соотношению посевных площадей и сельскохозяйственных культур:
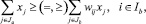
где wij – компонента пропорциональности между отдельными сельскохозяйственными культурами; Ja – множество переменных в соответствии с использованием сельскохозяйственных культур в севооборотах; Ib – множество ограничений в соответствии с севооборотными требованиями.
3. По группам кормов:
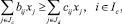
где bij – выход i-го вида кормовых единиц в расчете для единицы измерения j-й растениеводческой отрасли; cij – необходимость i-го вида одной головы j-го вида скота в группе кормов; Jc – множество переменных в соответствии с кормопроизводством; Jd – множество переменных в соответствии с животноводческой отраслью; Ic – множество ограничений в соответствии с кормовым балансом.
4. По производству и использованию сельскохозяйственной продукции:
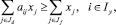
где aij – выход продукции i-го вида в расчете для единицы измерения j-й отрасли; Jd – множество переменных в соответствии с видами отраслей животноводства; Jf – множество переменных в соответствии с видами реализуемой продукции; Iy – множество ограничений в соответствии с производством и с использованием продукции.
5. По гарантированному объему производства сельскохозяйственной продукции:
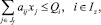
где Qi – гарантируемый объем производства продукции; Iz – множество ограничений в соответствии с гарантированным производством продукции.
6. По определению совокупной выручки:
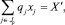
где qj – выход товарной продукции в денежном выражении для единицы j-й отрасли; Jp – множество переменных в соответствии с суммированием выручки от реализации продукции.
6. По определению производственных затрат:
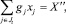
где gj – затраты материальных средств в денежном выражении для единицы j-й отрасли; Jt – множество переменных в соответствии с суммированием себестоимости сельскохозяйственной продукции.
7. Критерий неотрицательности переменных:
Любое накладываемое ограничение соответствует использованию производственных ресурсов, что в свою очередь позволяет обеспечить балансовую увязку количества n-ресурсов с их наличием в сельскохозяйственной организации.
Степень развития производственного, n-ресурсного потенциалов для каждой сельскохозяйственной организации определяется совокупностью переменных. Единицами измерения переменных в модели являются не только натуральные показатели (гектары, центнеры), но и стоимостные показатели.
Также при построении оптимизационных моделей необходимо учитывать, что все функционирующие в административных границах сельскохозяйственные организации имеют заданные почвенно-климатические условия и, соответственно, для них должны быть определены равные экономические обстоятельства. Также нужно обратить внимание на то, что при построении для отдельной сельскохозяйственной организации моделей производства присущи альтернативность развития при одинаковом начальном объеме вовлеченных ресурсов.
В итоге решения оптимизационной задачи предполагается полный учет и колебаний урожайности культур, и продуктивности животных, и всех производных от экономических показателей (производительности труда, себестоимости и цены реализации производимой продукции).
Для ориентации на максимально возможный уровень эффективности при определении перспектив развития сельскохозяйственных организаций необходимо учитывать реальные результаты и задействованные производственные n-ресурсы. Следовательно, имеется неодинаковость в модельных вариантах, что предполагает внесение коррекции уровней урожайности культур и продуктивности сельскохозяйственных животных, денежных расходов и цен реализации сельскохозяйственной продукции с учетом официального уровня инфляции [1].
Также в итоге получаемые оптимизационные модели позволяют обнаружить наиболее оптимальные величины производства различных видов сельскохозяйственной продукции и их комбинацию между собой. Для каждой сельскохозяйственной организации в процессе проведения расчетов определяются:
– размеры и состав отраслей сельскохозяйственного производства и их рациональное соответствие в общем количестве;
– распределение с учетом требований севооборота основных сельскохозяйственных культур;
– поголовье скота, обеспеченного полноценными кормами и помещениями содержания, объемы кормового производства и его использования, оптимальные рационы в кормлении животных;
– величины производства продукции отраслей растениеводства и животноводства и ее реализации;
– основные результативные показатели финансово-экономической деятельности [2].
Установление двойственных оценок для производства сельскохозяйственной продукции и для использования производственных ресурсов сопровождается решением главной задачи.
Таким образом, построение моделей, предложенных в исследовании, позволяет выявить вариант, оптимальный для сочетания структур сельскохозяйственного производства, и на этой базе размеры объемов производства продукции для сельскохозяйственных организаций в перспективе. Исполнение рассчитанных оптимальных вариантов на практике, как следствие, приведет к стабильному увеличению прибыли, обеспечению рентабельной работой сельскохозяйственных товаропроизводителей, которую можно направить на расширение и развитие производства и на удовлетворение социальных потребностей.
Практическое осуществление составленных моделей, в соответствии с предварительными оценками, позволит уменьшить расходы на производство сельскохозяйственной продукции и, соответственно, улучшить финансовый результат как показатель успешного ведения аграрными организациями хозяйственно-производственной деятельности.
Также применение результатов моделирования поможет выделить те приоритетные перспективы деятельности сельскохозяйственных организаций, которые следует развивать с учетом имеющихся климатических условий, культурных и национальных традиций сельского населения и его производственной квалификации.
Рецензенты:
Коледин С.В., д.э.н., профессор, заведующий кафедрой «Экономика АПК», филиал, Уральский государственный экономический университет, г. Челябинск;
Пряхин Г.Б., д.э.н., профессор кафедры «Экономика и управление», ФГБОУ ВПО «Уральский государственный университет физической культуры», г. Челябинск.
Работа поступила в редакцию 12.11.2014.
Источник: fundamental-research.ru
Математическое моделирование развития малого бизнеса в регионах России тема диссертации и автореферата по ВАК РФ 08.00.13, кандидат экономических наук Абдуллаев, Габид Шаванович
Оглавление диссертации кандидат экономических наук Абдуллаев, Габид Шаванович
Глава 1. Становление и развитие малых предприятий в регионах России
1.1. Проблемы развития малого бизнеса и пути их решения
1.2. Малые предприятия Республики Дагестан: анализ состояния и пути развития
1.3. Анализ существующих подходов к исследованию функционирования и развития малого предпринимательства
Глава 2. Экономико-математическое моделирование конъюнктуры рынка труда малого бизнеса
2.1. Механизм формирования спроса и предложения труда в сегменте малого предпринимательства
2.2. Спецификация макроэкономической модели рынка труда как системы одновременных эконометрических уравнений
2.3. Эконометрические методы идентификации параметров модели и особенности их применения на панельных данных
Глава 3. Эконометрический анализ развития малого бизнеса в регионах России в условиях трансформирующейся экономики
3.1. Статистический анализ динамики развития малого предпринимательства
3.2. Методология формирования исходных данных и описательная статистика
3.3. Идентификация параметров модели спроса и предложения труда и экономический анализ результатов расчетов
3.4. Оценка связей и зависимостей в малом бизнесе методами эко-нометрического моделирования
Рекомендованный список диссертаций по специальности «Математические и инструментальные методы экономики», 08.00.13 шифр ВАК
Малое предпринимательство трансформируемой России: региональные факторы активизации 2011 год, доктор экономических наук Басарева, Вера Гаврииловна
Математическое моделирование региональной дифференциации инновационной деятельности 2010 год, кандидат экономических наук Дегтярева, Анастасия Александровна
Многоуровневые модели зависимости экономического роста от инвестиций: эконометрический подход 2007 год, кандидат экономических наук Гафарова, Елена Аркадьевна
Влияние малого предпринимательства на состояние и динамику локальных рынков труда в российской экономике 2015 год, кандидат наук Саляхов, Эльдар Фанильевич
Статистическое исследование предложения труда женщин и уровня рождаемости в Российской Федерации 2008 год, кандидат экономических наук Родионова, Лилия Анатольевна
Введение диссертации (часть автореферата) на тему «Математическое моделирование развития малого бизнеса в регионах России»
Актуальность темы исследования. Опыт развитых стран показывает, что малые предприятия играют одну из ключевых ролей в экономике этих стран, выполняя ряд важнейших социально-экономических функций, таких как обеспечение занятости, формирование конкурентной среды, поддержание инновационной активности, смягчение социального неравенства, внедрение новых технологий. Доля малого бизнеса в ВВП развитых стран составляет 50% и выше.
Малый бизнес представляет достаточно крупный сектор российской экономики. Однако, несмотря на государственную поддержку, его развитие в последние годы тормозится: резкий подъем начала 90-х годов развития малого бизнеса сменился к концу столетия стагнацией. Доля его в ВВП страны в 2002 г. составила всего 12% (на уровне регионов этот показатель варьирует от 0,5% до 25%).
По нашему мнению стагнация развития малого бизнеса в России является результатом дифференциации процесса образования МП в регионах и объясняется неодинаковыми условиями создания собственного бизнеса. Детерминантами таких различий являются региональные риски, в том числе связанные с неоднородностью целей региональных органов власти и управления, отсутствием заметных преимуществ в занятости на МП, дифференциация населения в результате реформ.
При разработке мероприятий государственной поддержки малого бизнеса необходимо учитывать факторы, оказывающие существенное влияние на процесс возникновения новых малых предприятий. Также при формировании региональных программ развития малого бизнеса надо учитывать склонность населения к предпринимательству.
Существуют различные экономико-математические методы и модели исследования развития малого бизнеса в России. Они позволяют выявить особенности функционирования этого сегмента экономики и предсказывать его динамику в будущем при изменении каких-либо параметров. Однако большинство известных методов и моделей не всегда позволяют определить причины возникновения зависимостей, не дают возможности находить управленческие воздействия, которые бы обеспечивали наиболее эффективное развитие динамических процессов, дать рекомендацииi по обоснованию оптимальных стратегий4 развития предпринимательства.
Указанные нерешенные задачи и определяют актуальность и практическую значимость диссертационного исследования.
Степень разработанности проблемы. Проблемам развития малого бизнеса, вопросам маркетинговой, финансовой, хозяйственной и инвестиционной деятельности, институциональным особенностям развития, формам государственной финансовой его поддержки посвящены научно-исследовательские работы как российских, так и зарубежных ученых, в частности: Бабаевой JI.B., Блиновой Т.А., Данилиной Я.В., Ивановой Н.Ю., Норта Д., Радаева В.В., Рыбиной М.Н., Шахбанова Р.Б., Aslund А., Backberg Е., Baumol W.J., Brown D., DeJong D., Earl J., Johnson S., Kihlstrom R., Laffont J.J., Mason C.M., Reynolds, P.O., Storey D. и др.
В работах Айвазяна С.А., Басаревой В.Г., Егоровой Н.Е., Клейнера Г.Б., Колесниковой JI.A., Журавской Е.В., Лапиной Г.П., Майна Е.Р., Маренного М.А., Мхитаряна B.C., Орлова А.И., Попова В.М., Сонина K.A., Хачатряна С.Р., Amin А., Baumol W., Berkowitz D., Sakova Z. и др. освещены вопросы экономико-математического моделирования малого бизнеса на уровне отдельных предприятий, модели исследования операций^ прогнозирования развития, финансово-инвестиционного состояния деятельности субъектов малого бизнеса, региональных рисков, инвестиционной привлекательности и инвестиционного потенциала, сравнительного анализа внешней среды развития малого бизнеса.
Однако выполненные исследования либо относятся к начальному периоду развития предпринимательства в России, либо используют в качестве статистической базы только пространственные данные или только временные ряды.
На основании обзора и анализа известных исследований можно заключить, что вопросы построения эконометрических моделей для изучения проблем дифференциации регионов по предпринимательской активности и определения факторов, влияющих на эту активность в конце 90-х начале 2000-х гг. остается малоисследованной.
Объектом исследования является сектор малого предпринимательства в экономике России и, в частности, республике Дагестан.
Предмет исследования — динамические процессы функционирования сферы малого бизнеса и, в частности, рынка труда.
Цель и задачи исследования. Целью исследования является разработка эконометрических моделей для анализа факторов, влияющих на предпринимательскую активность на макро и мезо уровнях, выявления региональных различий в уровне развития малого бизнеса, а так же отраслевых различий в республике Дагестан.
Для достижения цели в работе были поставлены и решены следующие задачи: раскрыть экономическую сущность малого предпринимательства, определить основные направления деятельности малых предприятий и обобщить формы создания малых предприятий, выявить существенные факторы и сдерживающие ограничения развития малого бизнеса в России; разработать модель относительного спроса-предложения агрегированного сегмента малого предпринимательства в разрезе регионов и построить состоятельные и эффективные оценки ее параметров на панельных данных;
-выполнить эконометрический анализ динамики развития малого предпринимательства по регионам России по наиболее важным показателям и выявить факторы, определяющие дифференциацию регионов по уровню развития малого предпринимательства,^
-построить одно- и многофакторные эконометрические модели, характеризующие связи и зависимости между показателями развития малого бизнеса в разрезе регионов страны, с помощью которых дать оценку особенностей различных групп регионов.
-оценить динамику структурных изменений в отраслях малых предприятий республики Дагестан.
Теоретическая и методологическая основа исследования. Теоретическую основу диссертационной работы составили исследования российских и зарубежных ученых в области формирования механизмов развития малого бизнеса в современных российских условиях. Методологической основой исследования является системный подход к процессам формирования и развития малого бизнеса, методы математической статистики и эконометрики, математического моделирования экономических систем.
Инструментарно-методический аппарат исследования. Для решения поставленных в диссертационной работе задач использовались инструментальные программные средства: Microsoft Excel 2000, Stata 7.0, SAS.
Работа выполнена в рамках пунктов 1.4 «Разработка и исследование моделей и математических методов анализа микроэкономических процессов и систем: отраслей народного хозяйства, фирм и предприятий, домашних хозяйств, рынков, механизмов формирования спроса и потребления .» и 1.8 «Математическое моделирование экономической конъюнктуры, деловой активности, определение трендов, циклов и тенденций развития» паспорта специальности 08.00.13 — математические и инструментальные методы экономики.
Информационно-эмпирическая база диссертационного исследования. При проведении исследования использованы статистические данные Госкомстата РФ по регионам Российской Федерации 1997-2002 гг., а так же данные государственного комитета по статистике республики Дагестан, индексы «Эксперт-РА» по оценке инвестиционного климата в регионах, индексы концентрации (Герфиндаля-Хиршмана) по выпуску и занятости, данные ЦЭФИР о концентрации выпуска и занятости в регионах РФ.
Научная новизна результатов исследования: для республики Дагестан проведен анализ показателей эффективности деятельности предприятий сферы малого бизнеса на основе анализа главных компонент и многомерной средней и выявлены отрасли с высоким потенциалом развития; разработана оригинальная, эконометрическая модель относительного спроса и предложения труда агрегированного сегмента малого предпринимательства в разрезе регионов, которая представляет собой систему одновременных уравнений, проведено оценивание этой системы различными методами (двухшаговый метод наименьших квадратов, трехшаговый метод наименьших квадратов и др.) на базе сформированных панельных данных по регионам России; на основе анализа результатов разработанных эконометрических моделей сделаны выводы о значимости институциональных факторов для развития предпринимательства в регионах России, наряду с факторами риска, предпринимательским и трудовым потенциалом населения, а также дан анализ региональных фиксированных эффектов спроса/предложения, временного эффекта и эффекта региональных особенностей субъектов Южного Федерального округа; разработаны одно- и многофакторные эконометрические модели, характеризующие связи и зависимости между технико-экономическими показателями развития малого бизнеса в разрезе регионов страны (объем выпуска продукции, численности занятых, объем инвестиций и др.), с помощью которых дана оценка особенностей различных групп регионов
Практическая значимость полученных результатов заключается в возможности применения разработанных моделей и рекомендаций при планировании и прогнозировании развития малого бизнеса с учетом региональных особенностей. Результаты исследования приняты для практического использования Комитетом Правительства Республики Дагестан по поддержке и развитию малого предпринимательства и потребительского рынка й Отделом потребительского рынка и развитию предпринимательства Администрации Госсовета и Правительства Республики Дагестан и подтверждены документами о внедрении.
Материалы диссертации использованы в преподавательской деятельности соискателя на экономических факультетах Дагестанского государственного университета при чтении курсов лекций по дисциплинам эконометрика, экономико-математические методы и модели, а также при разработке учебно-методических материалов к этим курсам.
Основные положения и результаты, выносимые на защиту:
1. Система мероприятий по под держке бизнеса в России и причин неприспособленности системы государственной поддержки малого предпринимательства, призванной обеспечить: оптимизацию нормативно-правовых основ регулирования малого предпринимательства со стороны государства, развитие системы финансовой поддержки малого предпринимательства, лизинг оборудования для восполнения нехватки высокотехнологичных основных фондов;
2. Система показателей относительной отраслевой доходности предприятий сферы малого бизнеса, сконструированная на основе анализа главных компонент и многомерной средней и позволяющая определить отрасли с высоким потенциалом развития;
3. Эконометрическая модель относительного спроса и предложения агрегированного сегмента малого предпринимательства в разрезе регионов России и результаты ее оценки;
4. Результаты эконометрического анализа о значимости институциональных факторов для развития предпринимательства в России, наряду с факторами риска, предпринимательским и трудовым потенциалом населения, региональных фиксированных эффектов спроса/предложения и временного эффекта;
5. Оценка региональных особенностей субъектов Южного Федерального округа в формировании сегмента малого бизнеса методами экономико-математического моделирования.
Внедрение и апробация результатов работы. Основные положения и результаты диссертационного исследования представлялись, обсуждались и получили положительную оценку на ХХ1Х-ХХХ1 Международных конференциях «Информационные технологии в науке, образовании, телекоммуникации, бизнесе 1Т+8Е» (Украина, Ялта-Гурзуф, 2002-2004); III Международной научно-практической конференции «Проблемы регионального управления, экономики, права и инновационных процессов в образовании» (Таганрог, 2003); I Международной научной конференции «Функционально-дифференциальные уравнения и их приложения» (Махачкала, 2003); IV Межвузовских научных чтениях «Математические и статистические методы в экономике и естествознании» (РГЭУ «РИНХ», Ростов-на-Дону, 2003); II- IV Региональных научно-практических конференциях «Компьютерные технологии в науке, экономике, образовании» (Махачкала, 2001-2003).
Публикации. Основные результаты диссертационного исследования опубликованы в 14 научных работах, в которых автору принадлежит 4,6 п.л.
Структура и объем работы. Диссертационная работа состоит из введения, трех глав, заключения, библиографии и 11 приложений. Текст занимает 130 страниц. Библиографический список литературы включает 123 источника.
Источник: www.dissercat.com
Экономико-математические методы и модели и их классификация
Экономико-математическое моделирование служит для того, чтобы описывать системные социально-экономические процессы в виде экономико-математических моделей. Опираясь на определения метода моделирования и модели, можно сделать вывод, что экономико-математические методы – это своеобразный инструмент, а экономико-математические модели – это специфический продукт процесса экономико-математического моделирования.
Классификация экономико-математических методов
Говоря об экономико-математических методах, стоит отметить, что для них характерна своя классификация. Эти методы являются комплексом экономико-математических дисциплин, которые представляют собой сплав экономики, математики и кибернетики. В силу этих обстоятельств классификация экономико-математических методов сводится к классификации научных дисциплин, из которых она состоит. Однако стоит отметить, что общая классификация этих дисциплин не выработана окончательно до настоящего момента. Максимально приближённо можно выделить следующие разделы:
- Экономическая кибернетика.
- Математическая статистика.
- Математическая экономика.
- Методы принятия оптимальных решений.
- Методы и дисциплины.
- Методы экспериментального изучения экономических явлений.
Экономическая кибернетика
Экономическая кибернетика занимается системным анализом экономики, теории экономической информации и теорией управляющих систем.
Математическая статистика
Математическая статистика изучает экономические приложения данной дисциплины, которые представлены в виде выборочного метода, дисперсионного анализа, корреляционного анализа, регрессионного анализа, многомерного статистического анализа, факторного анализа, теории индексов и др.
Математическая экономика занимается исследованием вопросов, касающихся количественной стороны эконометрики. Здесь теория экономического роста, а также теория производственных функций и межотраслевые балансы. Кроме этого национальные счета, анализ спроса и предложения, региональный и пространственный анализ и др.
Методы принятия оптимальных решений
Методы принятия оптимальных решений в первую очередь касаются исследований и операций в экономике. Это самый объёмный раздел, который состоит из дисциплин и методов. Сюда входит оптимальное математическое программирование, сетевые методы планирования и управления, программно-целевые методы планирования и управления и многое другое. Одновременно с тем, оптимальное математическое программирование включает в себя линейное программирование, дискретно программирование, дробно-линейное программирование, стохастическое программирование, геометрическое программирование и др.
Методы и дисциплины
Методы и дисциплины здесь подразумеваются как для отдельной, так и для планируемой экономики с единым центром, а также для рыночной или, конкурентной. Первые – это теория наилучшей работы экономики, лучшее планирование, теория оптимального ценообразования, модели материально-технического снабжения и др. Вторые – методы, которые дают возможность разрабатывать модели незамещенной конкуренции, модели капиталистического цикла, модели монополии, модели индикаторного планированы, модели теории фирмы и др. Большинство из методов, которые были разработаны для централизованно планируемой экономики, могут эффективно применяться и при экономико-математическом моделировании в условиях рыночной экономики.
Методы экспериментального изучения экономических явлений
К данным методам можно отнести математические методы анализа и планирования экономических экспериментов, в том числе методы машинной имитации, а также деловые игры. Кроме того, к ним относятся методы экспертных оценок, которые могут быть применены для оценки явлений с непосредственным измерением.
Классификация экономико-математических моделей
Сразу стоит сказать, что единой системы классификации математических моделей социально-экономических систем и процессов не существует, но чаще всего говорят о десяти признаках их классификации. Вот некоторые из них.
Согласно общего целевого назначения всякие экономико-математические модели можно поделить на теоретико-аналитические, которые применяются для исследования общих свойств и закономерностей экономических процессов, и прикладные, применение которых происходит в условиях решения конкретных экономических задач анализа, прогнозирования и управления.
В соответствии со степенью агрегирования объектов моделирования модели делятся на макроэкономические и микроэкономические. Но важно понимать, что чёткого разграничения данные модели не имеют.
Также модели делятся по конкретному предназначению, иными словами, по своей цели создания и использования. Так выделяют балансовые модели, которые отражают все требования соответствия наличия ресурсов и их применения; трендовые модели, в которых развитие моделируемой экономической системы иллюстрируется посредством тренда её основных показателей; оптимизационные модели, которые предназначены для выбора наилучшего варианта их определённого числа вариантов производства, распределения или потребления; имитационные модели, которые призваны использоваться для машинной имитации изучаемых систем или процессов.
Также модели делятся по типу информации, которая используется в ней на аналитические, построенные на априорной информации и идентифицируемые, которые строятся на апостериорной информации.
Кроме этого все модели делятся на статистические, которые не зависят от момента времени, и динамические, описывающие экономические системы в развитии.
Ещё одним критерием является учётный фактор неопределённости модели, и они разделяются на детерминированные, если для них характерен на выходе однозначный результат управляющих воздействий, и стохастические, если на конечный результат могут оказывать влияние различные случайные факторы.
Кроме этого экономико-математические модели классифицируются по характеру математических объектов, входящих в состав или, что по сути одно и то же, по типу математического аппарата, который применён в данной модели. Этот признак помогает выделить следующие модели: матричные, модели линейного и нелинейного программирования, корреляционно-регрессионные модели, модели теории массового обслуживания, модели сетевого планирования и управления, и др.
И, наконец, различают модели по тому, к какому типу в изучении социально-экономических связей они относятся. Здесь можно говорить о дескриптивных и нормативных моделях. Дескриптивные модели образуют модели, которые предназначены для описания и объяснения фактически наблюдаемых явлений или для прогноза таких явлений. В качестве примера дескриптивной модели можно выбрать балансовую или трендовую модель.
Нормативные модели изучают совершенно иное. Их интерес заключается не в исследовании того, как устроена и развивается экономическая система, а в том, как она должна быть устроена и работать в соответствии с некоторыми критериями.
Все оптимизационные модели относятся к типу нормативных, в качестве примера можно использовать нормативные модели уровня жизни.
В качестве примера можно привести модель отраслевого баланса в разрезе экономико-математической модели. Если опираться на все классификации, которые были приведены выше, то можно сделать вывод, данная классификация является прикладной и макроэкономической. Ещё одна характеристика – аналитическая модель с дескриптивной функцией, которая является детерминированной, балансовой и матричной моделью. Важно отметить, что несмотря ни на что существуют статические, и динамические модели ЭММ МОБ.
Источник: zaochnik-com.com
