Деньги, которыми вы располагаете сейчас, представляют большую ценность, чем деньги, которые у вас появятся позже. Чтобы определить эту разницу при оценке инвестиций, лучше всего подойдет показатель чистой приведенной стоимости (NVP).
Большинство людей знают, что деньги, которые у вас есть сейчас, более ценны, чем деньги, которые вы получите потом. Это связано с тем, что вы можете использовать их, чтобы заработать еще больше денег, управляя бизнесом, или купив что-то сейчас, чтобы продать это позже, или просто вкладывая деньги банк и зарабатывая проценты.
Будущие деньги также менее ценны, потому что инфляция снижает их покупательную способность. Это называется временной стоимостью денег.
Но как именно можно сравнить текущую стоимость денег со стоимостью денег в будущем?
Именно для этого финансисты рассчитывают чистую приведенную стоимость.
Что такое чистая приведенная стоимость?
Чистая приведенная стоимость или NPV (от англ. ‘Net Present Value’) представляет собой текущую стоимость денежных потоков, с учетом требуемой нормы доходности вашего проекта, по сравнению с вашими первоначальными инвестициями.
Что такое чистая приведенная стоимость (NPV)?
На практике NPV — это метод оценки доходности инвестиций или рентабельности инвестиций для проекта или капитальных расходов. Рассматривая все будущие денежные потоки, которые вы ожидаете от инвестиций, и переводя эти потоки в сегодняшнюю стоимость, вы можете решить, выгоден ли проект.
Для чего обычно компании используют NPV?
Когда менеджеру нужно сравнивать проекты и решить, какие из них следует одобрить, у него обычно есть три инструмента:
- внутренняя норма доходности (IRR),
- срок окупаемости (PP или ‘payback period’) и
- чистая приведенная стоимость (NPV).
Показатель чистой приведенной стоимости — это выбор большинства финансовых аналитиков. На это есть две причины.
- Во-первых, NPV учитывает временную стоимость денег, т.е. переводит будущие денежные потоки в сегодняшние деньги.
- Во-вторых, он дает конкретное число, которое менеджеры могут использовать, чтобы легко сравнить первоначальные денежные затраты с текущей денежной отдачей.
Показатель NPV намного превосходит метод окупаемости (PP), который также часто используется.
Привлекательность показателя PP заключается в том, что его легко вычислить и просто понять: когда вы вернете деньги, которые вы вложили? Но он не принимает во внимание то, что покупательная способность денег сегодня больше, чем покупательная способность той же суммы денег в будущем.
Это то, что делает NPV превосходным методом оценки инвестиций. К счастью, сегодня с помощью финансовых калькуляторов и электронных таблиц NPV почти так же легко вычислить, как и PP.
Менеджеры также используют NPV, чтобы решить, делать ли крупные закупки, например, оборудования или программного обеспечения. Он также используется в слияниях и поглощениях (хотя в этом сценарии NPV называется моделью дисконтированных денежных потоков).
NPV, приведенная стоимость и дисконтирование на примере
Фактически, это модель, которую использует Уоррен Баффет для оценки компаний.
Каждый раз, когда компания использует сегодняшние деньги для получения будущей прибыли, можно смело применять NPV.
Как рассчитать NPV?
Сегодня почти никто не вычисляет NPV каноническим способом. В Excel есть функция NPV, которая упрощает работу, когда вы ввели свой денежный поток расходов и доходов. (Откройте в Excel справку по функции «NPV», и вы получите мини-учебник по расчету этого показателя).
Многие финансовые калькуляторы также включают функцию NPV.
Тем не менее, даже если вы не математический ботаник, полезно понять математику этого коэффициента. Даже опытные аналитики могут не помнить или понимать математику, хотя это довольно просто.
Расчет выглядит следующим образом (см. Формулу 1):
- (CF_n) = ожидаемый чистый денежный поток за год (n).
- (N) = прогнозируемая длительность инвестиций или количество лет в рассматриваемом периоде.
- (r) = ставка дисконтирования или альтернативная стоимость капитала.
В результате мы получаем сумму текущей (приведенной) стоимости денежных потоков (положительных и отрицательных) за каждый год, дисконтированную таким образом, чтобы она отражалась в сегодняшней стоимости денег.
Чтобы сделать это вручную, вы сначала вычисляете текущую стоимость прогнозируемых денежных потоков за каждый год периода и делите его на ((1 + r)) в степени, равной количеству лет в периоде.
Таким образом, для 5-летнего денежного потока расчет для каждого года этого 5-летнего периода выглядит следующим образом:
То есть, вы рассчитываете этот показатель для каждого из этих 5 лет, а затем суммируете полученный результаты за каждый год. Это и будет текущая стоимость всех ваших прогнозируемых доходов. Затем вы вычитаете свои первоначальные инвестиции из этого числа, чтобы получить NPV.
Если NPV отрицательный, то проект нерентабелен.
В конечном итоге это приведет к утечке денежных средств из бизнеса. Однако, если показатель положительный, проект можно принять. Чем больше положительное число, тем больше выгода для компании.
Теперь вам будет интересно побольше узнать о ставке дисконтирования.
Ставка дисконтирования (от англ. ‘discount rate’) специфична для компании, поскольку она связана с тем, как компания ведет свою основную деятельность. Это норма прибыли, которую ожидают инвесторы от компании, или стоимость заимствования денег.
Если акционеры ожидают 12-процентного дохода, то это и есть ставка дисконтирования, которую компания будет использовать для расчета NPV. Если фирма выплачивает 4% по ее долгу, то она может использовать эту цифру в качестве ставки дисконтирования. Как правило, эту ставку определяет финансовый директор и его служба.
Каковы распространенные ошибки, которые делают люди при расчете NPV?
Есть две вещи, о которых следует знать при использовании NPV.
Во-первых, этот показатель трудно объяснить другим, то есть нефинансовым специалистам.
Дисконтированная стоимость будущих денежных потоков — это не та фраза, которую можно легко удалить из нефинансового языка.
Тем не менее, этот показатель стоит лишних усилий, чтобы объяснить его. Любая инвестиция, которая проходит тест NPV, увеличит акционерную стоимость, а любые инвестиции, которые не прошли этот тест, (если они будут осуществлены), непременно повредят компании и ее акционерам.
Второе, о чем должны помнить менеджеры, заключается в том, что расчет NPV основан на нескольких предположениях и оценках, а это значит, что он может быть субъективен и подвержен ошибкам. Вы можете уменьшить риски, дважды проверив свои оценки и сделав анализ чувствительности после того, как сделали свой первоначальный расчет.
Есть три узких места, где вы можете сделать ошибочные оценки, которые резко повлияют на конечные результаты вашего расчета.
- Первоначальные инвестиции.
Знаете ли вы, сколько проект или расходы будут стоить? Если вы покупаете оборудование, имеющее фиксированную цену, то риска нет.
Но если вы обновляете свою ИТ-систему и планируете затраты на персонал в зависимости от сроков и этапов проекта, а также собираетесь делать предполагаемые закупки, суммы могут быть достаточно условными. - Риски, связанные со ставкой дисконтирования.
Вы используете сегодняшнюю ставку и применяете ее к будущим доходам, поэтому есть вероятность, что в третьем году проекта процентные ставки будут увеличиваться, а стоимость ваших средств повысится.
Это будет означать, что ваши доходы за этот год будут менее ценными, чем вы изначально думали. - Прогнозируемые результаты вашего проекта.
Именно здесь финансовые аналитики часто ошибаются в оценке. Вы должны быть относительно уверены в прогнозируемых результатах вашего проекта.
Эти прогнозы, как правило, оптимистичны, потому что люди ХОТЯТ сделать проект или ХОТЯТ купить оборудование.
Источник: fin-accounting.ru
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin.
ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : » ИНФРА — М «, Издательство » ВесьМир «. Дж . Блэк .)
Примечание1 . Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется ЧПС() , то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с Приведенной стоимостью .
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет : при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи Приведенная стоимость .
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу сложных процентов .
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция ЧПС() (английский вариант — NPV()). В ее основе используется формула:
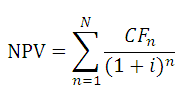
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2 . Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить: Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год) . Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
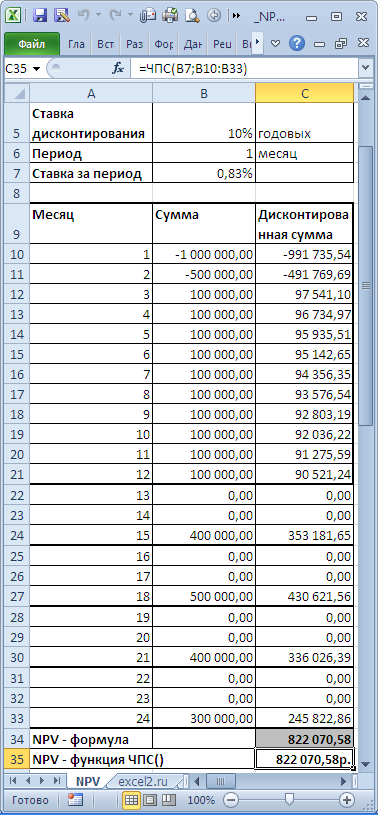
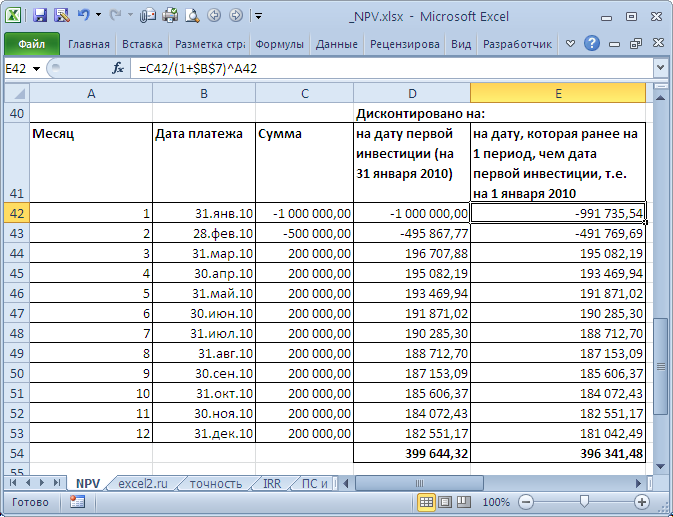
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ). Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
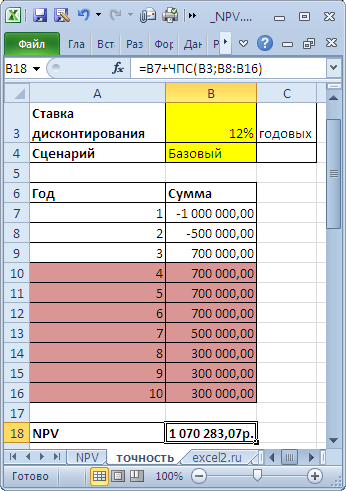
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
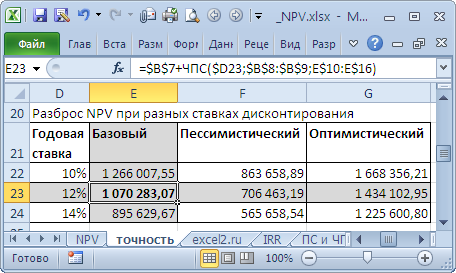
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
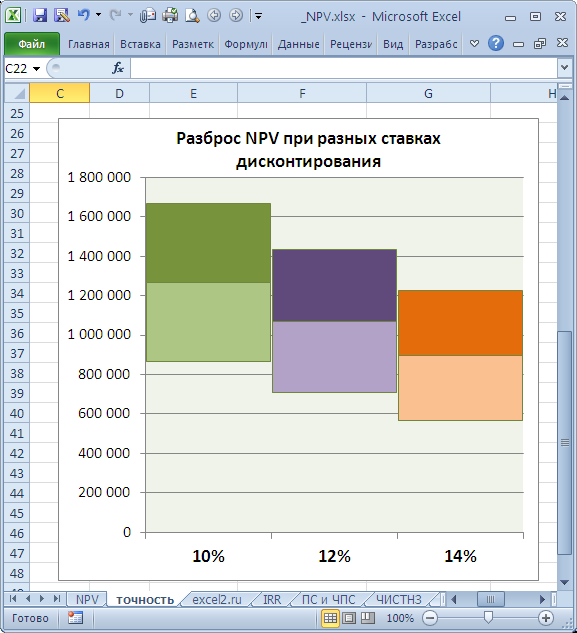
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом).
С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
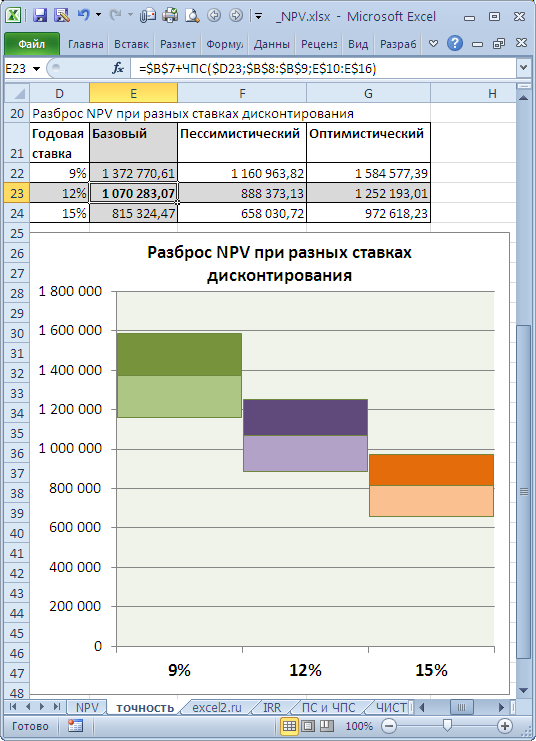
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Внутренняя ставка доходности (англ. internal rate of return , IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см. файл примера, лист IRR ).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
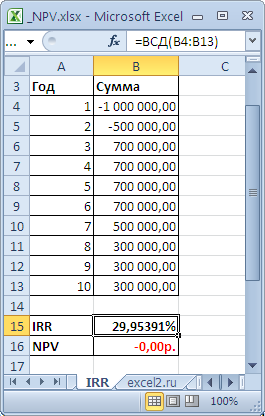
Для расчета IRR используется функция ВСД() (английский вариант – IRR()). Эта функция тесно связана с функцией ЧПС() . Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией ВСД() , всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле: =ЧПС(ВСД(B5:B14);B5:B14)
Примечание4 . IRR можно рассчитать и без функции ВСД() : достаточно иметь функцию ЧПС() . Для этого нужно использовать инструмент Подбор параметра (поле «Установить в ячейке» должно ссылаться на формулу с ЧПС() , в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).
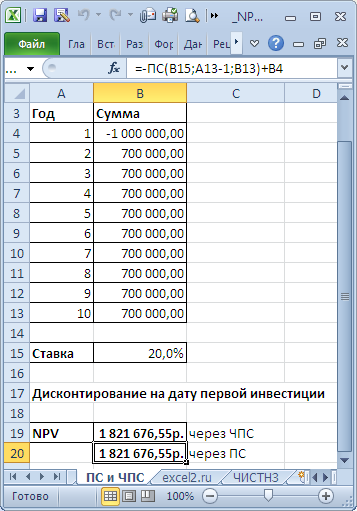
В этом случае все денежные потоки (диапазон В5:В13 , 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке В4 . Ставка дисконтирования расположена в ячейке В15 со знаком минус. В этом случае формула =B4+ЧПС(B15;B5:B13) дает тот же результат, что и = B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).
Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
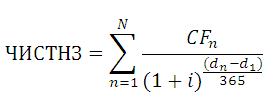
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от ЧПС() является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у ЧИСТНЗ() всегда годовая, т.к. указана база 365 дней, а не за период, как у ЧПС() . Еще отличие от ЧПС() : все денежные потоки всегда дисконтируются на дату первого платежа.
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций ЧИСТНЗ() и ЧПС() . Эти функции возвращают несколько отличающиеся результаты. Для задачи из файла примера, Лист ЧИСТНЗ разница составила порядка 1% (период = 1 месяцу).
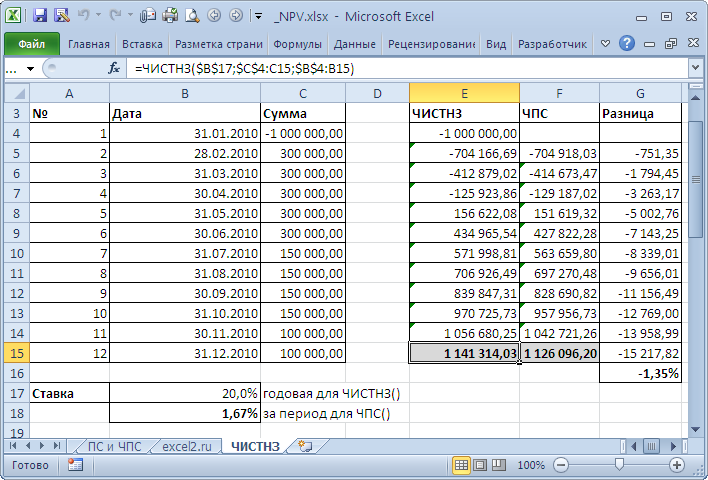
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с ЧПС() , у которой имеется родственная ей функция ВСД() , у ЧИСТНЗ() есть функция ЧИСТВНДОХ() , которая вычисляет годовую ставку дисконтирования, при которой ЧИСТНЗ() возвращает 0.
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
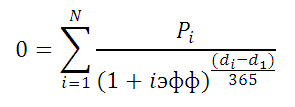
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Примечание5 . Функция ЧИСТВНДОХ() используется для расчета эффективной ставки по потребительским кредитам .
Источник: excel2.ru
Расчет NPV

NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков. Если вы хотите вложить деньги в перспективный бизнес-проект, то неплохо было бы для начала рассчитать NPV этого проекта. Алгоритм расчета такой:
- нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем;
- определить стоимость капитала (англ. Cost of Capital) для вас — это будет ставкой дисконтирования;
- продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2);
- Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта.
Если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.
Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы:
- возместить инвестированный капитал и
- обеспечить необходимый доход на этот капитал.
Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем прибыльнее является данный проект для инвестора. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.
Расчет NPV. Пример
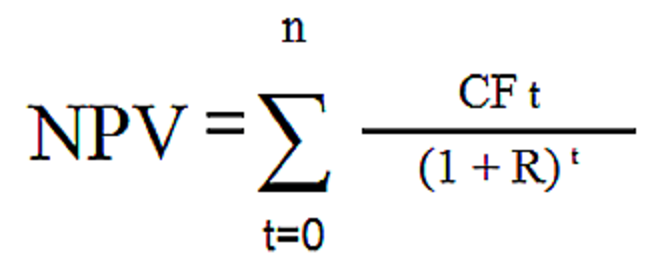
Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
где
- n, t — количество временных периодов;
- CF — денежный поток (англ. Cash Flow);
- R — стоимость капитала, она же ставка дисконтирования (англ. Rate).
На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта A и B, которые имеют следующую структуру денежных потоков на ближайшие 4 года:
Таблица 1. Денежный поток проектов A и B.
| 0 | ($10,000) | ($10,000) |
| 1 | $5,000 | $1,000 |
| 2 | $4,000 | $3,000 |
| 3 | $3,000 | $4,000 |
| 4 | $1,000 | $6,000 |
Оба проекта A и B имеют одинаковые первоначальные инвестиции в $10,000, но денежные потоки в последующие годы сильно разнятся. Проект A предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект B, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта A, но зато в последующие два года Проект B принесет больше денежных средств, чем проект A. Рассчитаем NPV инвестиционного проекта.
Для упрощения расчета предположим:
- все денежные потоки случаются в конце каждого года;
- первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас;
- стоимость капитала (ставка дисконтирования) составляет 10%.
Напомним, что для того, чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».
Применим формулу NPV для Проекта A. У нас четыре годовых периода и пять денежных потоков. Первый поток ($10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:
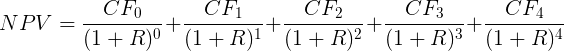
Если подставить в эту сумму данные из таблицы для Проекта A вместо CF и ставку 10% вместо R, то получим следующее выражение:
![]()
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока. В результате приведенная стоимость денежных потоков для проекта A равна $788,2. Расчет NPV для проекта A можно так же представить в виде таблицы и в виде шкалы времени:
Таблиц 2. Расчет NPV для проекта A.
| 0 | ($10,000) | 1 | 1 | ($10,000) |
| 1 | $5,000 | 1 / (1.10) 1 | 0.9091 | $4,545.5 |
| 2 | $4,000 | 1 / (1.10) 2 | 0.8264 | $3,305.8 |
| 3 | $3,000 | 1 / (1.10) 3 | 0.7513 | $2,253.9 |
| 4 | $1,000 | 1 / (1.10) 4 | 0.6830 | $683.0 |
| ИТОГО: | $3,000 | $788.2 |

Рисунок 1. Расчет NPV для проекта А.
Аналогичным образом рассчитаем NPV для проекта B.
![]()
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших ($4,000 и $6,000), но отдалённых по времени (годы 3 и 4) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта B чистая приведенная стоимость денежных потоков будет меньше, чем для проекта A. Наши расчеты NPV для проекта B дали результат — $491,5. Детальный расчет NPV для проекта B показан ниже.
Таблиц 2. Расчет NPV для проекта A.
| 0 | ($10,000) | 1 | 1 | ($10,000) |
| 1 | $1,000 | 1 / (1.10) 1 | 0.9091 | $909.1 |
| 2 | $3,000 | 1 / (1.10) 2 | 0.8264 | $2,479.2 |
| 3 | $4,000 | 1 / (1.10) 3 | 0.7513 | $3,005.2 |
| 4 | $6,000 | 1 / (1.10) 4 | 0.6830 | $4,098.0 |
| ИТОГО: | $4,000 | $491.5 |
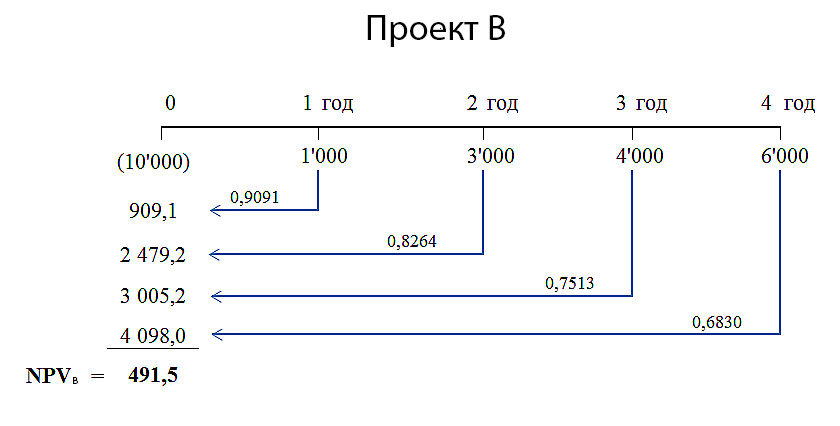
Рисунок 2. Расчет NPV для проекта B.
Вывод
Оба эти проекта можно принять, так как NPV обоих проектов больше нуля, а, значит осуществление этих проектов приведет к увеличению доходов компании-инвестора. Если эти проекты взаимоисключающие и необходимо выбрать только один из них, то предпочтительнее выглядит проект A, поскольку его NPV=$788,2, что больше NPV=$491,5 проекта B.
Тонкости расчета NPV
Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала, то вы легко сможете подставить их в формулу и рассчитать NPV. Но на практике не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.
Денежные потоки
Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.
Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.
Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.
Ставка дисконтирования
Ставка дисконтирования в формуле расчета NPV — это стоимость капитала для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы. В общем случае компания может получить финансирование из трех источников:
- взять в долг (обычно у банка);
- продать свои акции;
- использовать внутренние ресурсы (например, нераспределенную прибыль).
Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств. Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке.
Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.
Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC (Weighted Average Cost of Capital), что переводится как средневзвешенная стоимость капитала.
Зависимость NPV проекта от ставки дисконтирования
Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала. Давайте рассчитаем NPV по проектам A и B для разных ставок дисконтирования:
| 0 | $3,000 | $4,000 |
| 2 | $2,497.4 | $3,176.3 |
| 4 | $2,027.7 | $2,420.0 |
| 6 | $1,587.9 | $1,724.4 |
| 8 | $1,175.5 | $1,083.5 |
| 10 | $788.2 | $491.5 |
| 12 | $423.9 | ($55.3) |
| 14 | $80.8 | ($562.0) |
| 16 | ($242.7) | ($1,032.1) |
| 18 | ($548.3) | ($1,468.7) |
Таблица 3. Зависимость NPV от ставки дисконтирования.
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):
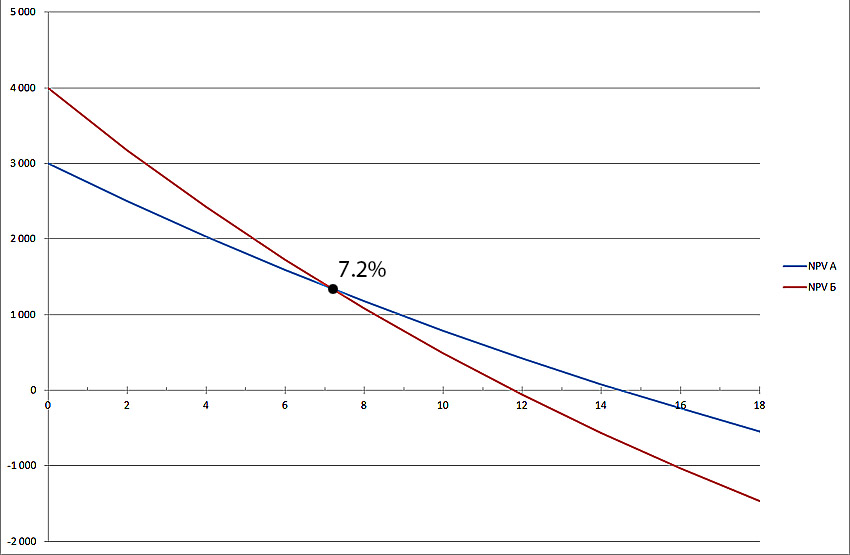
Рисунок 3. Зависимость NPV от ставки дисконтирования.
Из графика видно, что NPV проекта A превышает NPV проекта B при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.
Кроме того, из графика также видно, что проект B является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта B уменьшается быстрее по мере роста этой ставки. И это легко объяснимо. В проекте B денежные поступления в первые годы проекта невелики, со временем они увеличиваются.
Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.
Например, можно рассчитать, чему будут равны $10,000 через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения.
Таблица 4. Зависимость NPV от времени его возникновения.
| 1 | $9,524 | $9,091 | $433 | 4.5% |
| 4 | $8,227 | $6,830 | $1,397 | 17.0% |
| 10 | $6,139 | $3,855 | $2,284 | 37.2% |
В последнем столбце таблицы видно, что один и тот же денежный поток ($10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37.2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать.
Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.
Алексей Голубицкий, компания Alawar
Источник: forpm.ru
