Модель роста Гордона — простая и широко признанная модель дисконтирования дивидендов (DDM). Рассмотрим формулы, особенности, а также практические примеры расчетов и применения модели роста Гордона, — в рамках изучения инвестиций в фондовый рынок по программе CFA.
Довольно очевидная проблема, которая возникает, когда кто-то пытается применить Формулу 1 к оценке обыкновенного акционерного капитала, заключается в том, что эта формула требует, чтобы аналитик оценивал бесконечную последовательность ожидаемых дивидендов.
Чтобы упростить этот процесс, аналитики обычно делают предположения о том, как дивиденды будут расти, или изменяться со временем.
Модель постоянного роста Гордона или просто модель роста Гордона (англ. ‘Gordon constant growth model’) — это простая и широко признанная модель дисконтирования дивидендов (DDM). Эта модель предполагает, что дивиденды растут бесконечно с постоянным темпом.
Благодаря допущению о постоянном темпе роста, модель роста Гордона особенно хорошо подходит для оценки акций компаний, выплачивающих дивиденды, которые относительно нечувствительны к бизнес-циклу и находятся в стадии зрелости. Примеры таких компаний могут включать энергетическую отрасль, которую отличает медленный рост, или производство продуктов питания первой необходимости (например, хлеба).
3 1 Модель дисконтированных дивидендов видео фрагмент 1
Исторические данные о стабильном темпе роста дивидендов являются еще одним практическим критерием, если аналитик считает, что эта схема роста сохранится в будущем.
При допущении о постоянном росте Формулу 1 можно представить в виде Формулы 8, где (g) является постоянным темпом роста:
Если допустить, что требуемая ставка доходности (r) всегда превышает темп роста (g), то выражение в квадратных скобках в Формуле 8 представляет собой бесконечную геометрическую прогрессию и ее сумма сводится к:
Если мы подставим это выражение в Формулу 8, то получим модель роста Гордона, представленную Формулой 9:
Для иллюстрации этой формулы предположим, что текущие (самые последние) годовые дивиденды на акцию составляют €5.00 и ожидается, что дивиденды будут расти на 4% в год. Требуемая ставка доходности на инвестированный капитал составляет 8%.
Следовательно, оценка действительной стоимости с использованием модели роста Гордона составит:
Обратите внимание, что числителем является (D_1), а не (D_0): использование неправильного числителя является распространенной ошибкой.
Модель роста Гордона оценивает действительную стоимость как приведенную стоимость растущего перпетуитета. При темпе роста (g) равном 0, Формула 8 сводится к выражению для приведенной стоимости перпетуитета, как было показано ранее в Формуле 6.
При оценке долгосрочных темпов роста аналитики используют различные методы, в том числе прогнозирование роста дивидендов или прибыли с использованием медианного темпа роста, а также с использованием Формулы 10 для оценки устойчивого темпа роста:
( Large g = b times ROE ) (Формула 10)
- (g) = темп роста дивидендов
- (r) = коэффициент удержания прибыли = (1 — коэффициент выплаты дивидендов)
- ROE = доходность собственного (акционерного) капитала
Пример 7 иллюстрирует применение модели роста Гордона к акциям крупной промышленной производственной компании. Аналитик считает, что они продолжат свой рост с темпом, которого они достигли в предыдущие три года, и останутся стабильными в будущем.
В этом примере необходимо определить, насколько темп роста дивидендов увеличит оценку действительной стоимости. Этот вопрос связан оценкой, поскольку если темп роста высок в процентном выражении, то большая часть стоимости акций зависит от реализации оценки роста.
На этот вопрос можно ответить, вычитая из оценки действительной стоимости ( полученной с помощью Формулы 9) результат по Формуле 6, который предполагает отсутствие роста дивидендов.
Соответствующая концепция — приведенная стоимость роста возможностей (PVGO, ‘present value of growth opportunities’), обсуждается в дальнейших чтениях.
Пример (7) применения модели роста Гордона.
Компания Siemens AG работает в технологической сфере и производит капитальные продукты. Она работает в отраслях инжиниринга, производства, автоматизации, энергетики и транспортировки.
Siemens AG работает по всему миру и является одной из крупнейших компаний в своих секторах. Она также является крупным работодателем, как на внутреннем немецком рынке, так и в десятках других стран мира.
Выдержка финансовой информации о Siemens представлена в Иллюстрации 3.
Источник: fin-accounting.ru
Модель Гордона (Gordon Growth Model)
Модель постоянного роста (Dividend Discount Model, DDM) – это модель, в которой предполагается, что дивиденды будут расти от периода к периоду в одной пропорции, т.е. с одинаковым темпом роста. Данная модель широкое распространение получила под названием модель Гордона (Gordon Growth Model).
Модель названа в честь М. Дж. Гордона (M.J. Gordon), который первоначально опубликовал ее в совместном с Эли Шапиро (Eli Shapiro) исследовании: Capital Equipment Analysis: The Required Rate of Profit, Management Science, 3(1) (October 1956).
Как мы знаем, формула дисконтирования предполагает, что приведенная стоимость акции PV (определяющая ее цену в исходный момент времени) может быть представлена в виде:

М. Дж. Гордон для упрощения расчетов предположил: поскольку срок действия акции теоретически не ограничен, считаем, что поток денежных выплат представляет собой бесконечный поток дивидендов (ликвидационной суммы уже не будет, так как акция существует бесконечно долго). Кроме того Гордон предложил считать все величины ставки прироста ежегодных выплат (g) одинаковыми, т. е. дивиденды возрастают ежегодно в (1+g) раз, причем величина (g) не меняется до бесконечности. С учетом этого допущения формула примет вид [2]:
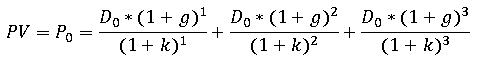
Таким образом, расчет стоимости в соответствии с моделью Гордона производится по формуле:

Кроме вышеуказанных упрощений, модель Гордона предполагает что:
- Величина k должно быть всегда больше g, в противном случае цена акции становится неопределенной. Это требование вполне логично, так как темп прироста дивидендов g может в какой-то момент превысить требуемую норму отдачи акции k. Однако это не произойдет, если полагать выбранный срок дисконтирования бесконечным, ибо в данном случае дивиденды постоянно прирастали бы более высокими темпами, чем норма отдачи акции, что невозможно.
- Предприятие должно выплачивать дивиденды регулярно, в противном случае модель Гордона неприменима. Более того, требование неизменности величины g означает, что компания направляет на выплату дивидендов всегда одну и ту же долю своего дохода.
- Требование неизменности величин k и g вплоть до бесконечности ограничивает структуру капитала предприятия: считается, что единственным источником финансирования фирмы являются ее собственные средства, а внешние источники отсутствуют. Новый капитал поступает в компанию только за счет удерживаемой доли дохода, чем выше доля дивидендов в доходе предприятия, тем ниже уровень обновления капитала.
Применение модели Гордона в оценке бизнеса
При оценке бизнеса, при прогнозировании доходов, в связи с тем, что свободный денежный поток не подается прогнозированию более чем на несколько лет вперед, введены положения о природе изменения этих денежных потоков – предполагается оценка остаточной (терминальной) стоимости
бизнеса на дату окончания явно выраженного прогнозного периода.
Согласно модели Гордона производиться капитализация годового дохода постпрогнозного периода в показатель стоимости при помощи коэффициента капитализации, рассчитанного как разница между ставкой дисконтирования и долгосрочными темпами прироста (модель Гордона используется в рамках доходного подхода).
При отсутствии темпов роста коэффициент капитализации будет равен ставке дисконтирования.
Расчет конечной стоимости в соответствии с рассматриваемой моделью производится по следующей формуле[1]:

Относительный размер терминальной стоимости увеличивается по мере уменьшений продолжительности прогнозного периода и становится весомой величиной по мере удаления горизонта прогноза. В зависимости от ставки дисконтирования для прогнозов свыше 10 лет терминальная стоимость становится гораздо менее существенным элементом.
Суть модели Гордона заключается в следующем: Стоимость компании на начало первого года постпрогнозного периода равна величине капитализированного дохода постпрогнозного периода (т.е. сумме стоимостей всех ежегодных будущих доходов в постпрогнозном периоде).
При слишком высоких темпах прироста прибыли модель Гордона использовать нельзя, так как такие показатели возможны при значительных дополнительных инвестициях, которые эта формула не учитывает.
В практическом руководстве А. Грегори [3], эта модель, будучи модифицирована для расчета капитала, принимает следующий вид:
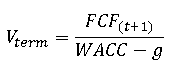
Чтобы найти текущую стоимость предприятия, надо эту терминальную стоимость дисконтировать по среднему WACC и прибавить к текущей стоимости всех показателей свободных денежных потоков за конкретный прогнозный период.
При использовании этой формулы важно понять, как используются разумные предположения о показателе g, долговременном (до бесконечности) темпе роста.
Модель Гордона может использовать историческую, текущую или прогнозируемую прибыль, и нередко последний показатель рассчитывается путем умножения прибыли, полученной в последний период, на ожидаемый долгосрочный темп роста, в этом случае формула примет вид:
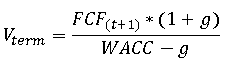
Ограничения при использовании модели Гордона:
- темпы роста дохода компании должны быть стабильны;
- темпы роста дохода не могут быть выше ставки дисконтирования;
- капитальные вложения в постпрогнозном периоде должны быть равны амортизационным отчислениям (для случая, когда в качестве дохода выступает денежный поток).
- Астраханцева И.А. Учет и анализ: Учеб.пособие / ФГБОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина. — Иваново, 2014. — 344с.
- Асаул А.Н. Основы бизнеса на рынке ценных бумаг: учебник / А.Н. Асаул, Н.А. Асаул, Р.А. Фалтинский; под ред. д-ра экон. наук, профессора А.Н. Асаула. — СПб.: АНО «ИПЭВ», 2008. — 207с.
- Грегори А. Стратегическая оценка компаний (Практическое руководство) — М.: Квинто-Консалтинг, 2003. — 224 с.
- Дворец Н.Н. Оценка стоимости предприятия (бизнеса): Учебно-методическое пособие. — М.: МАРТИТ, 2008. — 136 с.
- Каллаур Н.А. Дивиденды организации // Экономико-правовой бюллетень. 2008. №12. — 160 с.
Источник: afdanalyse.ru
Модель гордона, формула, расчёт и пример

Модель Гордона — это метод расчета внутренней стоимости акций, исключая текущие рыночные условия. Модель представляет собой метод оценки, предназначенный для определения стоимости акции на основе дивидендов, выплачиваемых акционерам, и темпов роста этих дивидендов. Также её называют: модель роста гордона, модель дисконтирования дивидендов (DDM), модель постоянных темпов роста. Калькулятор здесь.
Модель была названа в честь профессора Майрона Дж. Гордона в 1960-х годах, но Гордон был не единственным финансовым ученым, который популяризировал модель. В 1930-х годах Роберт Ф. Вайз и Джон Берр Уильямс также проделали значительную работу в этой области.
Существует две основные формы модели: стабильная модель и модель многоступенчатого роста.
Стабильная модель
Стоимость акции = D1 / (k — g)
D1 = ожидаемый годовой дивиденд на акцию в следующем году
k = ставка дисконтирования или требуемая норма прибыли
g = ожидаемый темп роста дивидендов (обратите внимание — полагается, что он будет постоянен)
Т.е. данная формула позволяет вычислять будущую стоимость акции, через дивиденд, но при условии, что темп роста дивиденда будет одинаков.
Многоступенчатая модель роста
Если ожидается, что дивиденды не будут расти с постоянной скоростью, инвестор должен оценивать дивиденды за каждый год отдельно, включая ожидаемый темп роста дивидендов за каждый год. Тем не менее, многоступенчатая модель роста предполагает, что рост дивидендов в конечном итоге становится постоянным. Ниже будет пример.
Примеры
Стабильная (устойчивая) модель Гордона
Предположим, компания XYZ намерена выплатить дивиденды в размере 1 долл. США на акцию в следующем году, и вы ожидаете, что в дальнейшем она будет увеличиваться на 5% в год. Предположим также, что требуемая норма прибыли на акции компании XYZ составляет 10%. В настоящее время акции компании XYZ торгуются по 10 долларов за акцию. То есть ещё раз:
— планируется дивиденд 1 доллар на акцию
— дивиденд будет расти на 5% в год
— норма прибыли 10%
— сейчас цена акции 10 долларов
Теперь, используя формулу выше, мы можем рассчитать, что внутренняя стоимость одной акции акций компании XYZ равна:
$1.00 / (0.10 — 0.05) = $20
Таким образом, согласно модели, акции компании XYZ стоят 20 долларов за акцию, но торгуются по 10 долларов; Модель роста Гордона предполагает, что акции недооценены.
Стабильная модель предполагает, что дивиденды растут с постоянной скоростью. Это не всегда реалистичное предположение, потому как дела в компаниях всё же меняются, сегодня у них всё чудесно и они платят хорошие дивиденды, а завтра не платят их вовсе. Поэтому данный способ, со стабильной моделью, когда дивиденд каждый год один и тот же — всё же уступает место многоступенчатой модели роста.
Многоступенчатая модель роста Гордона
Предположим, что в течение следующих нескольких лет дивиденды компании XYZ будут быстро расти, а затем будут расти стабильными темпами. Ожидается, что дивиденды в следующем году по-прежнему составят 1 доллар на акцию, но дивиденды будут увеличиваться ежегодно на 7%, затем на 10%, затем на 12%, а затем увеличиваться на 5% постоянно. Используя элементы устойчивой модели, но анализируя каждый год отдельно, мы можем рассчитать текущую справедливую стоимость акций компании XYZ.
Исходные данные:
g1 (темп роста дивидендов, год 1) = 7%
g2 (темп роста дивидендов, год 2) = 10%
g3 (темп роста дивидендов, год 3) = 12%
gn (темп роста дивидендов в последующие годы) = 5%
Поскольку мы оценили темп роста дивидендов, мы можем рассчитать фактические дивиденды за эти годы:
D2 = $1.00 * 1.07 = $1.07
D3 = $1.07 * 1.10 = $1.18
D4 = $1.18 * 1.12 = $1.32
Затем рассчитываем приведенную стоимость каждого дивиденда в течение необычного периода роста:
$1.00 / (1.10) = $0.91
$1.07 / (1.10) 2 = $0.88
$1.18 / (1.10) 3 = $0.89
$1.32 / (1.10) 4 = $0.90
Затем мы оцениваем дивиденды, возникающие в период стабильного роста, начиная с расчета дивиденда за пятый год:
D5 = $1.32 * (1.05) = $1.39
Затем мы применяем формулу модели роста Гордона со стабильным ростом к этим дивидендам, чтобы определить их стоимость на пятый год:
$1.39 / (0.10-0.05) = $27.80
Приведенная стоимость этих дивидендов за период стабильного роста рассчитывается следующим образом:
$27.80 / (1.10) 5 = $17.26
Наконец, мы можем добавить текущую стоимость будущих дивидендов компании XYZ, чтобы получить текущую внутреннюю стоимость акций компании XYZ:
$0.91 + $0.88 + $0.89 + $0.90 + $17.26 = $20.84
Многоступенчатая модель роста также указывает на то, что акции компании XYZ недооценены (внутренняя стоимость в 20,84 доллара по сравнению с торговой ценой в 10 долларов).
Аналитики часто включают предполагаемую цену и дату продажи в эти расчеты, если они знают, что не будут удерживать акции бесконечно. Также купонные выплаты могут использоваться вместо дивидендов при анализе облигаций.
Вывод
Модель роста Гордона позволяет инвесторам рассчитать стоимость акций без учета текущих рыночных условий. Это исключение позволяет инвесторам сравнивать компании в различных отраслях, и по этой причине модель Гордона является одним из наиболее широко используемых инструментов анализа и оценки акций. Тем не менее, некоторые относятся к ней скептически.
Математически, чтобы сделать модель Гордона эффективной, необходимы два обстоятельства. Во-первых, компания должна выплачивать дивиденды. Во-вторых, темп роста дивидендов (g) не может превышать требуемую норму прибыли инвестора (k). Если g больше k, результат будет отрицательным, и акции не могут иметь отрицательных значений.
Модель Гордона, особенно многоступенчатая модель роста, часто требует от пользователей делать несколько нереалистичных и сложных оценок темпов роста дивидендов (g). Важно понимать, что модель чувствительна к изменениям g и k, и многие аналитики проводят анализ чувствительности, чтобы оценить, как различные предположения меняют оценку. В соответствии с моделью Гордона, акции становятся более ценными, когда их дивиденды увеличиваются, требуемая норма прибыли инвестора уменьшается, или ожидаемая скорость роста дивидендов увеличивается. Модель роста Гордона также подразумевает, что цена акций растет с той же скоростью, что и дивиденды.
Источник: a2-finance.com
