Сложный процент иногда кажется волшебством. На самом деле это мощный инструмент выращивания капитала, а секрет — в раскрытии силы на долгих сроках. Весь процесс похож на снежный ком, который в начале процесса приходится долго катать, раздражаясь медленным процессом и малозаметным результатом. Однако со временем каждая прокрутка дает видимый результат: на большую поверхность базы снежного кома прилипает новый слой снега; на выращенную базу капитала — копейки, рубли, тысячи и миллионы. На примере конкретных кейсов, таблиц и графиков Виктория Староватова, основатель Capital Acceleration Systems, идеолог антихрупких финансовых систем, рассказывает о применении сложного процесса в обычной жизни.

Основатель Capital Acceleration Systems
Что такое сложный процент
Предположим, что вы вложили 1 000 рублей под 10% годовых. Через год эта сумма приросла на 100 рублей и составила 1 100 рублей. Вы не стали забирать процентный доход, оставив всю сумму под те же 10%. Прирост за второй год составит уже 110 рублей, а вся сумма — 1 210 рублей. Процент на процент и есть сложный процент: проценты реинвестируются и участвуют в создании новой прибыли.
Что такое сложный процент? Капитализация.
С каждым годом «снежный ком» процентов раскручивается — поговорим об этом подробнее на примере больших сумм и сроков. А пока — короткий экскурс в историю.
Немного истории
Авторство слов о том, что сложный процент является восьмым чудом света, обычно приписывают Ротшильду, Рокфеллеру или Эйнштейну, но исторического подтверждения этому нет. Впервые фраза появилась в рекламе «The Equity Savings умножить полученную сумму на тот же коэффициент для второго года и так далее до желаемого срока.
Подсчет сложного процента на калькуляторе на 5 лет
Формула сложного процента выглядит так:
SUM = X × (1 + %) n , где: SUM — конечная сумма; X — начальная сумма; % — процентная ставка, процентов годовых ÷ 100; n — количество периодов, лет (месяцев, кварталов). Пример 1 Вы положили один миллион рублей на 5 лет и ожидаете 10% годовых. Какая сумма будет у вас в конце срока? Рассчитаем по формуле сложного процента: SUM = 1 000 000 × (1 + 10 ÷ 100) 5 = 1 610 510 рублей.
Можно ли увеличить доходность?
Структура первоначального портфеля с учетом колебаний стоимости акций, облигаций, паев будет меняться со временем. Ребалансировка, то есть покупка активов, чья доля снизилась, и продажа тех, чья доля увеличилась, с целью возврата к изначальной долевой структуре повысит доходность на 1–2% годовых. Проводить ее нужно регулярно: 1–2 раза в год. Кажется, что 1–2% — это очень мало.
Но на больших сроках и суммах это дает ощутимую разницу. Вернемся к нашему примеру, но добавим ребалансировку.
Пример 2 Вы положили один миллион рублей на 5 лет и ожидаете 10% годовых. Ежегодная ребалансировка привносит еще 2%. Какая сумма будет у вас в конце срока? Рассчитаем по формуле сложного процента: SUM = 1 000 000 × (1 + (10+2) ÷ 100) 5 = 1 762 342 рублей. Дополнительные 2% за 5 лет принесли 151 832 рубля.
Сложный процент | Что такое сложные проценты простыми словами, формула и расчёт сложных процентов
Куда идти за сложным процентом: во вклады или ценные бумаги
Сложный процент хорошо работает и на доходности в 5–7% годовых — средней характеристике рублевых вкладов. А вот его эффективность на валютных вкладах приближается к нулю: текущие ставки варьируются в пределах 0,01—0,05%. Здесь мы практически умножаем ноль на ноль. Рост в рублевом эквиваленте происходит заметнее, но может растаять из-за динамики обменного курса и инфляции. У любых вкладов нет подъемной силы фондового рынка в долгосрочной перспективе.
Как внедрить сложный процент в жизнь
Таблица прогноза роста капитала на 20 лет выглядит абстрактно. Но если привязать ее к жизни конкретной семьи: разбить на пятилетки, прописать возраст родителей и детей, отметить важные вехи — в ней появится много смысла.
Станет видно, что поступление сына в вуз в 2030 году будет обеспечено капиталом конкретного размера, а капитал, выращенный к выходу на пенсию в 2040 году, позволит получать пассивный доход от инвестиций в определенном размере. В этой же таблице можно анализировать и сопоставлять несколько больших финансовых целей, двигать их по шкале времени.
Окажется, что покупку квартиры придется отложить на 3–5 лет, при этом позволить более дорогое обучение детей. Возможно, решением станет выделение дополнительных 20 тысяч рублей для ежемесячного инвестирования: тогда и престижный вуз будет по карману, и мечту о расширении не придется откладывать. Смущает долгосрочное планирование? С каждым годом прогнозы станут все более точными.
В любом случае, наличие плана с отклонениями от реальности лучше его полного отсутствия. План освещает путь к большим жизненным целям, мотивирует и позволяет не сбиться с пути. Феномен сложного процента — «добавляет ветер в паруса инвестора».
Источник: delovoymir.biz
Функция «Сложный процент FV»
В долгосрочных финансово-кредитных операциях, если сумма процентов не выплачивается сразу после их начисления, а присоединяется к первоначальной сумме (долгу), для наращения суммы ссуд применяют сложные проценты (компаудинг). Наращение по сложным процентам представляет собой последовательное реинвестирование средств, вложенных под простые проценты, на один период начисления. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. Наращенная сумма ссуды определяется по формуле

где FV — наращенная сумма ссуды через Глет; [1]
R — значение годовой ставки процента в виде десятичной дроби;
Т — срок начисления процентов в годах.
Данная функция позволяет определить будущую стоимость суммы, которой располагает инвестор для объекта бизнеса в настоящий момент времени исходя из предполагаемой годовой ставки процента (дохода), срока начисления процентов.
Выражение а = (1 + R) T называют фактором накопления единицы денежных средств, положенной на депозит, его значение зависит от величин R и Т. При увеличении годовой ставки R и периода времени Тпроисходит увеличение накоплений на одну единицу денежных средств ДС. Изменение фактора в зависимости от изменения R и Т приводит к существенному изменению фактора накопления. Например:
1) R = 15%; Т= 4 года, at = (1 + 0,15) 4 = 1,75.
В конце четвертого года накопления при годовой ставке процента 15% единица ДС будет равна 1,75 единицы ДС;
2) R = 25%, Т= 4 года, а2 = (1 + 0,25) 4 = 2,44.
В конце четвертого года накопления при годовой ставке 25% единица ДС будет равна 2,44 единицы ДС;
3) Л= 15%; Т= 5 лет, д3 = (1 + 0,15) = 2,01.
В конце пятого периода накопления при процентной годовой ставке 15% единица ДС будет равна 2,01 единицы ДС.
Если в течение года начисления процентов осуществляются несколько раз, то наращенная сумма определяется по формуле

где FV — сумма ссуды к погашению через Тлет;
S— начальная сумма ссуды;
R — годовая процентная ставка;
М — количество начислений процентов в год;
(М х Т) — число единичных периодов от момента вложения средств до момента его погашения.
Единичный период — это промежуток времени между двумя начислениями (капитализация) процентов. Величина (R : М) называется номинальной ставкой. Чем больше начислений в год, тем чаще происходит капитализация.
Пример 2. Стоимость земельного участка, на котором находится предприятие, равна 340 тыс. руб. В течение ближайших трех лет по прогнозу стоимость будет повышаться ежегодно на 15%. Определить прогнозную стоимость земельного участка через каждый год.

Через год стоимость земельного участка составит 391 тыс. руб., т.е. возрастет на 51 тыс. руб.

Через два года стоимость земельного участка составит около 450 тыс. руб. и по сравнению с первоначальной стоимостью увеличится на 109,65 тыс. руб.

Через три года стоимость земельного участка составит около 517 тыс. руб. и по сравнению с первоначальной стоимостью увеличится на 177,1 тыс. руб.
Пример 3. Банк предоставил предприятию для приобретения оборудования 300 тыс. руб. сроком на два года под 28% годовых. Проценты начисляются каждое полугодие. Определить сумму денежных средств, которую предприятие должно вернуть банку, и цену источника финансирования.
В данном примере число единичных периодов — 4(2×2), процентная ставка на полугодие (номинальная ставка) составит 14% (28% : 2). Сумма средств к погашению через два года:

На каждый рубль источников финансирования оборудования для объекта бизнеса приходилось 69 коп. финансовых издержек, в среднем на каждое полугодие — 0,1402 |(1 + 0,69) 1/4 — 1 ], или 14,02%.
Пример 4. Банк предоставил предприятию для приобретения основного средства кредит в размере 1600 тыс. руб. сроком на два года под 24% годовых, погашение кредита — каждый квартал. Определить сумму к погашению, сумму наращений на сложные проценты, цену источника финансирования.
В данном примере число единичных периодов — 8 (2 х 4), процентная ставка на квартал составляет 6% (R,„ = 24% : 4), или 0,06.
Сумма к погашению через два года:

Финансовые издержки по кредиту:

Цена источника финансирования:
Цкр = 950,16 : 1600 = 0,5939.
На каждый рубль источника финансирования объекта приходилось 59,39 коп. финансовых издержек, в среднем в квартал — 0,060004 |(1 + + 0,5939) l/s — 1], или 6%.
Чем больше начислений процентов в год, тем быстрее растет наращенная сумма.
Величина процентной ставки, которая позволяет получать такую же величину основной суммы при ежегодном начислении, называется эффективной ставкой процента. Рассмотрим ее расчет на следующем примере.
Пример 5. Инвестор поместил на депозит 500 тыс. руб. сроком на четыре года под 12% годовых. Определить накопленную сумму, если начисление процентов производится по формуле сложных процентов в конце года, в конце полугодия, в конце квартала, в конце месяца, в конце дня. Рассчитать эффективную ставку. Формулы для расчетов и результаты решения задачи представлены в табл. 3.1.
Расчет накопленной суммы денежных средств и эффективной ставки
Число начислений в год
Расчет суммы вклада через четыре года (годовая ставка R = 12%), тыс. руб.
FK, = 5x(l + R) 4 FV4 = 500 х (1 + 0,12) 4 = = 786,76
786,76 = 500 x (1 + ЛЭ|) 4 Лэ1 = (786,76 :500)’/ 4 — 1 = = 0,12, или 12%
2. Два раза (каждое полугодие)
FV4 = Sx |1 + (Л:2)| 4 * 2 FV4 = 500 х [ 1 + (0,12 : 2)| 4 * 2 = = 796,92
796,92 = 500 x (1 + Л,,) 4 R,2 = (796,92 :500) 1/4 — 1 = = 0,123599, или 12,36%
3. Четыре раза (каждый квартал)
FV4 = Sx |1 +(Л:4)| 4 ‘ 4 FV4 = 500 x [ 1 + (0,12 : 4)| 4 * 4 = = 802,35
802,35 = 500 x (1 + Л,3) 4 Л,з = (802,35 : 500) 1/4 — 1 = = 0,125508, или 12,55%
4. 12 раз (каждый месяц)
FV4 = Sx |1 +(R: 12)| 4 * 12 FV4 = 500 x [ 1 +(0,12: 12)] 4xl2 = = 806,11
806,11 =500 x(l + Л^) 4 Ryx = (806,11 : 500) l/4 — 1 = = 0,126824, или 12,68%
5. 365 раз (каждый день)
FV4 = Sx |1 + (7?: 365)| 4×365 FV4 = 500 x 11 + (0,12 : 365)| 4 * 365 = = 807,97
807,97 = 500 x (1 + Лз5) 4 Лэ5 = (807,97 : 500)’^ 4 — 1 = = 0,127473, или 12,74%
Расчетные данные показывают, что при одной и той же минимальной ставке 12% годовых увеличение числа начислений в год приводит к более быстрому увеличению первоначального вклада, следовательно, и к увеличению эффективной ставки.
При временной оценке денежных потоков используются стандартные функции сложного процента FV:
- 1) будущую стоимость аннуитета FVA
- 2) дисконтирование PV
- 3) текущую стоимость аннуитета PVA
- 4) периодический взнос в погашение кредита РМТ
- 5) периодический взнос на накопление фонда РМТФ.
Каждая из этих функций характеризует процесс изменения денежных средств, пока они остаются на депозитном счете. Начисленный процент не снимается с депозитного счета, а капитализируется. Каждая из этих функций используется при решении конкретных задач, связанных с источниками финансирования объектов бизнеса. Общая характеристика стандартных функций сложного процента представлена в табл. 3.2.
Характеристика стандартных функций сложного процента
Общая характеристика, назначение
1. Сложный процент FV; FV= G (S, R, Т, М)
Значение функции отражает процесс наращения — увеличения первоначальной суммы денег, положенной на депозит при накоплении по сложному проценту, в связи с присоединением процентов к первоначальной сумме; она позволяет решать задачи типа «Определить сумму денежных средств, которая будет выдана вкладчику банком, если на первоначальный взнос S в течение Тлет М раз в год будет начисляться годовая процентная ставка R»
2. Будущая стоимость аннуитета FVA; FVA = G2 (РМТ, R, Г, М)
Позволяет решать задачи типа «Определить размер денежных средств на счете вкладчика, если в течение Глет М раз в год вносить фиксированную сумму денежных средств (РМТ), а банк начисляет на хранящийся вклад R процентов годовых»
3. Дисконтирование — PV (реверсии); PV=G2(S, R, Т,М)
Значение показывает настоящую (приведенную) стоимость денежных средств, которые должны быть получены в будущем. Используется для решения задач типа «Определить размер денежных средств 5, который необходимо поместить на депозит сегодня, чтобы через Г лет при начислении М раз в год при годовой процентной ставке R накопить определенную сумму денежных средств PV»
- 4. Текущая стоимость аннуитета PVA PVA = G„
- (РМТ, R, Т, М)
Позволяет решать задачи типа «Определить размер денежных средств, которые необходимо поместить на депозит сегодня при годовой процентной ставке R, чтобы в течение Г лет М раз в год снимать со счета определенные равные суммы денежных средств РМТ»
Общая характеристика, назначение
5. Периодический взнос на погашение кредита РМТ РМТ= Gs (5, Л, Г, М)
Позволяет решать задачи типа «Определить равновеликий размер денежных средств, который можно снимать со счета в течение А»лет М раз в год, если известен первоначальный вклад S и процентная годовая ставка R»
6. Периодический взнос на накопление фонда РМТФ;
Источник: bstudy.net
Сложный процент, среднегодовая доходность, дисконтирование и приращение


Сложный процент, среднегодовая доходность, дисконтирование и приращение
В этой статье рассмотрим базовые понятия, которые пригодятся любому инвестору: сложный процент, среднегодовая доходность, дисконтирование и приращение. Google-таблица с формулами, используемыми в тексте, находится по ссылке.
Сложный процент – Восьмое Чудо Света
Сложные проценты — самая мощная сила в природе! Сложный процент – это Восьмое чудо света. Тот, кто понимает это — зарабатывает его, тот, кто не понимает — платит его. Альберт Эйнштейн

Альберт Эйнштейн знал силу сложных процентов
Сложный процент – эффект, когда процент в конце одного периода прибавляется к основной сумме и в следующий период процент уже начисляется на новую сумму. И такое действие может происходить на всем периоде инвестирования (прибыль реинвестируется).
Формула, если капитализация раз в год:
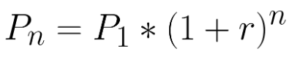
Пример: на три года инвестируем 100 000 рублей под ставку в 10% годовых. Капитализация раз в год. Проценты реинвестируются.
![]()
Формула, если капитализация несколько раз в год:
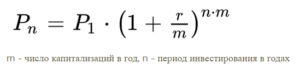
Пример: на три года инвестируем 100 000 рублей под ставку в 10% годовых, капитализация один раз в месяц. Проценты реинвестируются ежемесячно.
![]()
Сложный процент порождает иллюзию, что через 10-15-20-25-30 лет можно легко стать рантье и жить на проценты. Например, фондовый рынок дает 20% в год, у нас есть 30 лет и мы инвестируем 1 000 000 рублей. “Инвесторская сказка” может обещать следующее:
![]()
Инвестор “виртуально в будущем” с одного миллиона заработал 237 376 313 рублей.
Для среднестатистического человека это колоссальная сумма.
Что здесь не так?
Реальный сложный процент
Не так здесь то, что инфляция за это время составит тоже огромную величину. Для правильного восприятия роста благосостояния лучше считать эффекты сложного процента по реальной ставке (т.е. с учетом инфляции).
Например, если среднегодовая прогнозируемая инфляция составит 10%, то среднегодовая ожидаемая реальная доходность составит:
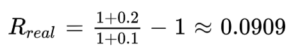
В итоге реальное благосостояние инвестора составит весомую, но не астрономическую сумму:
![]()
Инвестор становится богаче не в 237 раз, а в 13 раз! Это тоже отличный результат. К такому результату надо стремиться. В реальности очень трудно получать реальную доходность в 9% на протяжении длительного периода времени. В среднем можно получать реальную доходность от 3% до 9%.
Это не означает, что не нужно инвестировать. Это означает, что нужно смотреть правде в глаза.
Среднегодовая доходность
Для сравнения разных способов инвестиций на дистанции нам необходимо уметь считать среднегодовую доходность наших инвестиций. Формула при условии, что мы один раз инвестировали деньги и потом получили некий результат:
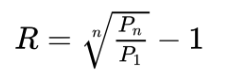
Пример: в 2014 году мы инвестировали на биржу 100 000 рублей. Через 3 года у нас на счету стало 285 000 рублей. Рассчитаем среднегодовую доходность за три года:
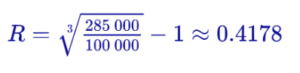
![]()
Экономический смысл: если бы выбирали между банком и биржей по доходности, то нам нужно было бы найти банк, который предлагает ставку в размере 41,78% или выше на протяжении 3 лет ежегодно.
Формула для расчета среднегодовой доходности, если нам известны результаты инвестиций по годам:
![]()
Пример: в первый год инвестор заработал 15%, во второй потерял -10% и в третий заработал 29%. Какова его среднегодовая доходность?
![]()
Несмотря на два очень удачных года среднегодовая доходность инвестора оказалась на уровне всего лишь 10,11%.
Периоды падения очень отрицательно сказываются на среднегодовой доходности!
Давайте ещё раз сделаем самопроверку и окончательно поймем экономический смысл. Посчитаем сначала с учетом ежегодной доходности по каждому году результат инвестирования:

Разница в 15 рублей получилась за счет округления 10,11%.
Плавная доходность лучше всплесков
Многие инвесторы (особенно новички) гонятся за огромными доходностями, получают их в один год и терпят “незначительные” убытки в следующий год. Давайте рассмотрим ещё один показательный случай из практики, что “медленные инвесторы” в итоге выигрывают:
Инвестор 1 получил доходность в первый год +90%, во второй год убыток в размере -21% и в третий год доходность в размере +15%.
Инвестор 2 получил доходность в первый год +21%, во второй год +32% и в третий год всего лишь +9%.
Кто заработал больше?
Среднегодовая доходность первого 19,96%.
Среднегодовая доходность второго 21,29%.
“Сверхдоходность” в 90% не спасла “быстрого” инвестора. Его итоговый результат оказался ниже, чем результат работы “плавного” инвестора.
Минусы вредны для портфеля. Если портфель упал на 20%, то ему надо заработать 25%, чтобы хотя бы восстановиться.
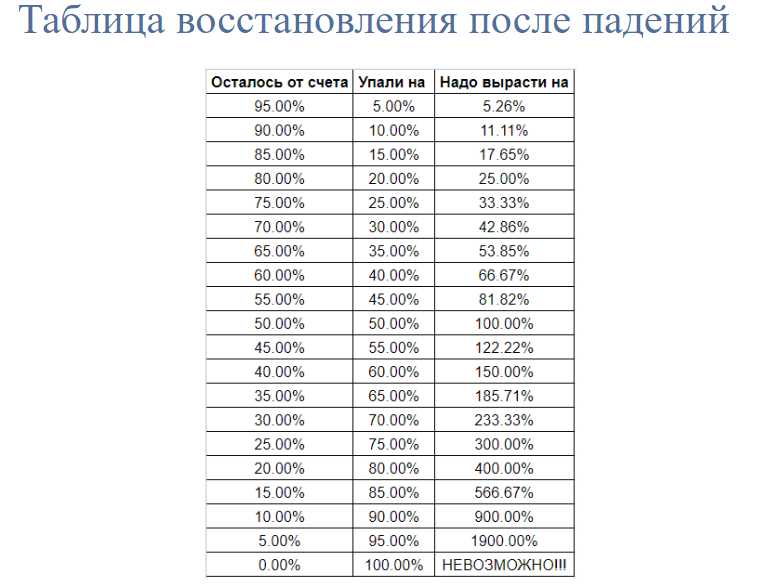
Сколько нужно зарабатывать после падений для восстановления первоначальной суммы на счете
Дисконтирование
Дисконтирование – это процесс определения текущей стоимости денег, когда известна их будущая стоимость. Дисконтирование дохода применяется для оценки будущих денежных поступлений (прибыль, проценты, дивиденды) с позиции текущего момента.
Дисконтирование выполняется путём умножения будущих денежных потоков (потоков платежей) на коэффициент дисконтирования:
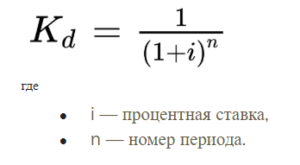
Экономический смысл дисконтирования (на примере)
Через 2 года Вам нужно будет 1 000 000 рублей, чтобы купить автомобиль. У Вас есть возможность положить деньги в банк под ставку 10%. Какой суммой денег нужно обладать сейчас, чтобы в будущем купить автомобиль?
![]()
Нам нужно будет 826 446,29 рублей, чтобы сейчас их инвестировать с доходность в 10% ежегодно и через 2 года снять 1 000 000 рублей.
826 446.29 * 1.1*1.1 = 1 000 000 рублей.
Наращение
Наращение – это процесс приведения текущей стоимости денег к будущей. Наращение позволяет получить оценку той суммы, на которую можно рассчитывать в будущем, инвестировав некоторым образом исходную сумму. Это процесс, обратный дисконтированию.
Базовая формула наращения, если ставка доходности одинакова для каждого периода:
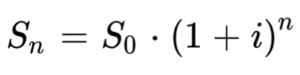
Экономический смысл наращения
Сейчас у нас есть 1 000 000 рублей. Мы хотим на 3 года его инвестировать на биржу, ожидаемая доходность инвестиций 15%. Какая сумма будет на счете через 3 года?
![]()
Наращение делают по сложному проценту. Возможно делать наращение по разным ставкам (в каждый период своя доходность).
По сути наращение и есть работа сложных процентов на будущие периоды.
Понимание силы сложных процентов позволяет более рассудительно и долгосрочно относиться к инвестициям.
Видеоверсия материала
(зарегистрируйтесь сейчас, воспользоваться можно будет позже)
Источник: www.finvavilon.ru
