Теория игр в экономике примеры в бизнесе

Здравствуйте, уважаемые читатели проекта Тюлягин! Сегодня мы рассмотрим такое понятие как теория игр. В статье кратко разбираем что это такое и в чем суть теории игр, где она применяется и как используется в экономике. Также поговорим о терминологии теории игр и таком понятии как равновесие Нэша. Кроме этого в статье также рассмотрены основные типы теории игр и примеры, включая дилемму заключенного, игру Диктатор, Ультиматум и другие.

• Что такое теория игр?
• Основы и суть теории игр

• Терминология теории игр
• Равновесие Нэша
• Влияние на экономику и бизнес

• Дилемма заключенного
• Игра Диктатор и Ультиматум
• Дилемма волонтера
• Игра Сороконожка

Что такое теория игр простыми словами

Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками. В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном процессе принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.

Ключевыми пионерами теории игр были математик Джон фон Нейман и экономист Оскар Моргенштерн в 1940-х годах. Многие считают математика Джона Нэша первым значительным продолжением работ фон Неймана и Моргенштерна.

Предполагается, что игроки в игре рациональны и будут стремиться максимизировать свои выигрыши в игре.

Основы и суть теории игр

В центре внимания теории игр находится игра, которая служит моделью интерактивной ситуации среди рациональных игроков. Ключ к теории игр состоит в том, что выигрыш одного игрока зависит от стратегии, реализованной другим игроком. Игра определяет личности, предпочтения и доступные стратегии игроков, а также то, как эти стратегии влияют на результат. В зависимости от модели могут потребоваться различные другие требования или предположения.

Теория игр имеет широкий спектр приложений, включая психологию, эволюционную биологию, войну, политику, экономику и бизнес. Несмотря на многочисленные достижения, теория игр по-прежнему остается молодой и развивающейся наукой.

Согласно теории игр, действия и выбор всех участников влияют на результат каждого.

Терминология теории игр

Каждый раз, когда у нас возникает ситуация с двумя или более игроками, которая связана с известными выплатами или поддающимися количественной оценке последствиями, мы можем использовать теорию игр, чтобы определить наиболее вероятные результаты. Начнем с определения нескольких терминов, обычно используемых при изучении теории игр:

• Игра: любое стечение обстоятельств, результат которого зависит от действий двух или более лиц, принимающих решения (игроков).
• Игроки: лицо, принимающее стратегические решения в контексте игры.
• Стратегия: полный план действий, который будет выполнять игрок с учетом набора обстоятельств, которые могут возникнуть в игре.
• Отдача: Выплата, которую получает игрок за достижение определенного результата. (Выплата может быть в любой форме количественно, из долларов в полезности.)
• Информационный набор: информация, доступная в определенный момент в игре (термин «информационный набор» чаще всего применяется, когда игра имеет последовательный компонент).
• Равновесие: момент в игре, когда оба игрока приняли свои решения и достигнут результат.

Равновесие Нэша

Равновесие Нэша — это результат, который, будучи достигнутым, означает, что ни один игрок не может увеличить выигрыш, изменив решения в одностороннем порядке. Равновесие также можно рассматривать как результат «без сожалений» в том смысле, что после того, как решение принято, игрок не будет сожалеть о решениях с учетом последствий.

Равновесие по Нэшу в большинстве случаев достигается со временем. Однако, как только равновесие Нэша достигнуто, отклонения от него не будет. После того, как мы узнаем, как найти равновесие по Нэшу, посмотрим, как одностороннее движение повлияет на ситуацию. Есть ли в этом смысл? Так не должно быть, и именно поэтому равновесие по Нэшу описывается как результат «без сожалений».

Как правило, в игре может быть более одного равновесия.

Однако это обычно происходит в играх с более сложными элементами, чем два выбора двух игроков. В одновременных играх, которые повторяются во времени, одно из этих множественных равновесий достигается после некоторых проб и ошибок. Этот сценарий различных вариантов выбора сверхурочно до достижения равновесия наиболее часто разыгрывается в деловом мире, когда две фирмы определяют цены на взаимозаменяемые продукты, такие как авиабилеты или безалкогольные напитки.

Влияние на экономику и бизнес

Теория игр произвела революцию в экономике, решив важнейшие проблемы предшествующих математических экономических моделей. Например, неоклассическая экономика изо всех сил пыталась понять ожидания предпринимателей и не могла справиться с несовершенной конкуренцией. Теория игр отвлекла внимание от устойчивого равновесия на рыночный процесс.

В бизнесе теория игр полезна для моделирования конкурирующего поведения экономических агентов. У предприятий часто есть несколько стратегических вариантов, которые влияют на их способность реализовать экономическую выгоду. Например, предприятия могут столкнуться с дилеммами, например: отказаться от существующих продуктов или разработать новые, снизить цены по сравнению с конкурентами или использовать новые маркетинговые стратегии. Экономисты часто используют теорию игр, чтобы понять поведение олигополистических фирм. Это помогает предсказать вероятные результаты, когда фирмы будут проявлять определенное поведение, например, сговор.

Двадцать теоретиков игр были удостоены Нобелевской премии по экономическим наукам за их вклад в эту дисциплину.

Типы теории игр

Хотя существует много типов теорий игр (например, симметричные / асимметричные, одновременные / последовательные и др.), наиболее распространенными являются теории кооперативных и некооперативных игр. Теория кооперативных игр изучает, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней задается вопрос, как формируются группы и как они распределяют выигрыш между игроками.

Теория некооперативных игр изучает, как рациональные экономические агенты взаимодействуют друг с другом для достижения своих собственных целей. Наиболее распространенной некооперативной игрой является стратегическая игра, в которой перечислены только доступные стратегии и результаты, являющиеся результатом комбинации вариантов выбора. Упрощенный пример реальной некооперативной игры — «Камень-ножницы-бумага».

Примеры теории игр

Теория игр анализирует несколько «игр». Ниже мы кратко опишем некоторые из них.

Дилемма заключенного

Дилемма Заключенного является наиболее известным примером теории игр. Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы их осудить. Однако, чтобы получить признание, чиновники выводят заключенных из одиночных камер и допросят каждого в отдельных камерах. Ни у одного из заключенных нет средств общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде квадрата 2 x 2.

1. Если оба признаются, каждый из них получит пятилетний тюремный срок.
2. Если заключенный 1 признается, а заключенный 2 — нет, то заключенный 1 получит три года, а заключенный 2 — девять лет.
3. Если заключенный 2 признается, а заключенный 1 — нет, то заключенный 1 получит 10 лет, а заключенный 2 — два года.
4. Если ни один из них не признается, каждый отсидит по два года тюрьмы.

Самая выгодная стратегия — не признаться. Однако ни один из них не осведомлен о стратегии другого, и без уверенности в том, что один из них не признается, оба, скорее всего, признаются и будут приговорены к пяти годам тюремного заключения. Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для всех вместе.

Выражение «зуб за зуб» (или «око за око») было определено как оптимальная стратегия для решения дилеммы заключенного. Стратегия «зуб за зуб» была введена Анатолем Рапопортом, который разработал стратегию, в которой каждый участник повторяющейся дилеммы заключенного следует курсом действий, совместимым с предыдущим ходом своего оппонента. Например, если его спровоцировать, игрок впоследствии ответит ответным ударом, если не спровоцировать, игрок сотрудничает.

Игра Диктатор и Ультиматум

Это простая игра, в которой игрок A должен решить, как разделить денежный приз с игроком B, который не участвует в принятии решения с игроком A. Хотя сама по себе эта стратегия не является теорией игр, она дает некоторые интересные сведения о поведении людей. Эксперименты показывают, что около 50% держат все деньги при себе, 5% делят их поровну, а остальные 45% дают другому участнику меньшую долю.

Игра в диктатора тесно связана с игрой в ультиматум, в которой Игроку А дается определенная сумма денег, часть которой должна быть отдана Игроку Б, который может принять или отклонить данную сумму. Загвоздка в том, что если второй игрок отклоняет предложенную сумму, ни A, ни B ничего не получают. Игры Диктатор и Ультиматум преподают важные уроки для таких вопросов, как благотворительность и филантропия.

Дилемма волонтера

В дилемме волонтера кто-то должен взять на себя рутинную работу или работу для общего блага. Наихудший возможный исход будет реализован, если никто не станет добровольцем. Например, рассмотрим компанию, в которой широко распространено мошенничество в области бухгалтерского учета, хотя высшее руководство об этом не подозревает. Некоторые младшие сотрудники бухгалтерии знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.

Признание разоблачителем также может иметь определенные последствия в будущем. Но если никто не станет добровольцем, крупномасштабное мошенничество может привести к банкротству компании и потере всех рабочих мест.

Игра Сороконожка

Игра «Сороконожка» — это обширная игра в теории игр, в которой два игрока поочередно получают шанс получить большую долю из медленно увеличивающегося денежного фонда. Игра устроена так, что если игрок передает тайник своему противнику, который затем забирает тайник, игрок получает меньшую сумму, чем если бы он взял банк.

Игра с сороконожкой завершается, как только игрок берет тайник, причем этот игрок получает большую часть, а другой игрок — меньшую часть. В игре заранее определено общее количество раундов, которое заранее известно каждому игроку.

Ограничения теории игр

Самая большая проблема теории игр состоит в том, что, как и большинство других экономических моделей, она основана на предположении, что люди являются рациональными субъектами, корыстолюбивы и стремятся максимизировать полезность. Конечно, мы социальные существа, которые действительно сотрудничают и заботятся о благополучии других, часто за свой счет. Теория игр не может объяснить тот факт, что в некоторых ситуациях мы можем попасть в равновесие по Нэшу, а в других случаях — нет, в зависимости от социального контекста и игроков.

Резюме

В какие «игры» играют в теории игр?

Это называется теорией игр, поскольку теория пытается понять стратегические действия двух или более «игроков» в данной ситуации, содержащей установленные правила и результаты. Хотя теория игр используется во многих дисциплинах, она чаще всего используется в качестве инструмента при изучении бизнеса и экономики. Таким образом, «игры» могут включать в себя то, как две конкурирующие фирмы отреагируют на снижение цен другой, если одна фирма приобретет другую, или как трейдеры на фондовом рынке могут отреагировать на изменение цен.

Теоретически эти игры можно отнести к категории подобных дилемм заключенного, игре диктатора, ястребу и голубю, Баху или Стравинскому, а также нескольким другим вариациям.

Каковы предположения об этих играх?

Как и многие экономические модели, теория игр также содержит набор строгих предположений, которые должны выполняться для того, чтобы теория делала хорошие прогнозы на практике. Во-первых, все игроки являются рациональными субъектами, максимизирующими полезность, которые имеют полную информацию об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но большинство игр будет рассматриваться в контексте только двух игроков.

Что такое равновесие по Нэшу?

Равновесие по Нэшу — это важная концепция, относящаяся к стабильному состоянию в игре, в котором ни один игрок не может получить преимущество путем одностороннего изменения стратегии, при условии, что другие участники также не меняют свои стратегии. Равновесие Нэша обеспечивает концепцию решения в некооперативной (состязательной) игре. Оно названо в честь Джона Нэша, получившего Нобелевскую премию в 1994 году за свою работу.

Кто придумал теорию игр?

Теория игр в значительной степени приписывается работам математика Джона фон Неймана и экономиста Оскара Моргенштерна в 1940-х годах и широко развивалась многими другими исследователями и учеными в 1950-х годах. По сей день теория игр остается областью активных исследований и прикладной науки.

• Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками и обеспечения оптимального принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.
• Используя теорию игр, можно разложить реальные сценарии для таких ситуаций, как ценовая конкуренция и выпуск продукции (и многое другое), и спрогнозировать их результаты.
• Сценарии включают дилемму заключенного и диктаторскую игру среди многих других.

А на этом сегодня все про Теорию Игр. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!

Источник: tyulyagin.ru

Как побеждать конкурентов на основе теории игр

В любой рыночной ситуации действовать можно по-разному. Какой вариант с наименьшими издержками приведет к нужной цели? Смоделируйте действия компаний-игроков – и вы это поймете.

Снова конкурент опустил цены на товар, который и так продается по себестоимости? Фирма-поставщик сделала отгрузку в непрофильную торговую сеть, и теперь за молотком и гвоздями идут не к вам, а в супермаркет? Зачем конкуренты и поставщики рушат рынок? И какой стратегии придерживаться в такой ситуации? Эти вопросы можно рассмотреть в теории игр.

Как вообще появилась концепция теории игр? В 1944 году Оскар Моргенштерн и Джон фон Нейман выпускают книгу «Теория игр и экономическое поведение», в которой впервые дают определение понятию «игра» и математически описывают поиск оптимальных стратегий. Эта наука живая и динамичная, имеет весьма широкое применение во многих сферах.

В своем современном варианте теория игр применяется в политике, экономике, социологии, бизнесе. Управление предприятием, конкуренция, принятие стратегических решений, управление рисками, стимулирование сбыта – все взаимодействия в данных разделах можно представить в виде игры. Игра в данном контексте – это прежде всего конфликт интересов. Чем же может помочь теория игр в борьбе с конкурентами?

Пример игры: «дилемма заключенного»

Рассмотрим «дилемму заключенного». Эту игру предложили в 1950 году американские математики Мерил Флад и Мелвин Дрешер. Есть мнение, что «дилемма заключенного» была разработана для прогнозирования гонки ядерных вооружений: в роли заключенных выступали СССР и США.

Постановка задачи следующая: поймали двух преступников на мелком хулиганстве, но подозревают в ограблении банка. Заключенные находятся в разных камерах. Полиция планирует допросить каждого отдельно и заставить сознаться в краже. Если никто не сознается, то оба получают срок за хулиганство – один год.

Если первый сознается, а второй – нет, то сознавшегося отпускают за сотрудничество, а «молчуна» запирают на десять лет. Если сознаются оба, то каждый получает срок в пять лет. Матрица игры выглядит следующим образом:

Заключенный 1; Заключенный 2

Молчать

Стучать

Выгоднее всего для обоих заключенных молчать, тогда каждый получит по году. Но, если подельник молчит, то логично его сдать и не получить срок вообще. А если он заговорит, то тогда тоже выгоднее сознаться. И так думает каждый.

Таким образом, в любом случае стратегия «стучать» для каждого «игрока» по отдельности является доминирующей. В этой дилемме существует равновесие – точка, из которой ни одному игроку не выгодно уходить, и оно в точке «стучать / стучать». Дилемма как раз в том, что выигрыш в доминирующей стратегии для каждой стороны меньше, чем вариант с учетом интересов всех игроков.

К сожалению, дилемма заключенного очень точно описывает рыночную конкуренцию. Компании-конкуренты смотрят друг на друга, словно узники демпинга, и опускают цены, не доверяя друг другу.

И ведь вот же оно, решение: давайте договариваться и держать уровень прибыли. Однако в пределах стратегии борьбы за потребителя, основанной на низкой цене, компании вынуждены ориентироваться прежде всего на ходы конкурентов. Особенно печальное зрелище представляет собой такая стратегия на падающем рынке.

Как же решить проблему? О дилемме заключенного написано более 2000 работ, однако всего разработано несколько вариантов решения:

1. Создать карающее правило, которое уберет стратегию предательства / снижения цен из доминирующих. Например, каждый раз после очередного падения цен со стороны одних конкурентов другие могут как-то влиять на них. Варианты для поставщиков: стоп-отгрузка, лишение маркетинговой поддержки или уменьшение скидки на закупку.

2. Выйти из дилеммы. То есть сделать так, чтобы у потребителя просто не было выбора. К подобной стратегии однажды прибегла GM на автомобильном рынке. Жесткая конкуренция привела к резкому падению цен на автомобили. Клиенты все чаще ориентировались на скидки, распродажи. Тогда GM выпустила кредитную карту, на которой накапливались ежегодные бонусы от покупок.

Потратить бонусы можно исключительно на автомобиль или обслуживание GM. Все акции компания отменила, а усилия направила на продвижение бонусной программы. Как результат, карты пользовались большой популярностью. За год держатель мог накопить до $3500 бонусов, и вопрос выбора марки автомобиля решен.

3. Подкорректировать свою стратегию во времени. До этого, описывая «дилемму заключенного», мы предполагали, что действие игры развивается в ограниченных временных рамках. Однако лучше соответствует реальности и интереснее с точки зрения вариантов исхода ситуация, когда компании уже имеют опыт предыдущих «игр».

Исследования Роберта Аксерольда показали, что при повторяющихся итерациях и большем количестве игроков стратегия «сдать / снизить цену» не работает. Точнее, она дает меньший результат. Оптимальной стратегией путем практических сессий была выбрана «око за око с прощением». Ее суть:

• Добропорядочность. Никогда первым не опускать цены.
• Мстительность. Отвечать ударом на удар конкурента, не давать спуска, держать контроль над ценами.
• Прощать. Отомстив конкуренту, возвращаться к сотрудничеству. Это предотвратит бесконечное понижение цен.
• Не завидовать. Не пытаться уничтожить конкурента любой ценой. Меньше смотреть на чужой бизнес, а больше – на свой! Не концентрироваться на том, чтобы прыгнуть выше и кинуть дальше. Придерживайтесь своей, уникальной стратегии.

Игроки в реальной рыночной ситуации

В нашей жизни часто возникают ситуации, которые можно формализовать с помощью теории игр. Рассмотрим практическую задачу.

Есть две конкурирующие розничные компании, будем называть их для простоты К1 и К2. К1 традиционно держит более высокие цены за счет сервиса, широкого ассортимента и уровня предоставляемых услуг, имеет несколько подразделений с высокими оборотами. К2 выбирает стратегию низких цен и имеет много небольших филиалов.

К2 узнает, что около одного из центральных филиалов К1 сдается помещение за 150 тыс. руб. К2 может открыть здесь свой филиал, буквально «дверь в дверь» с К1, и забрать часть клиентского потока за счет низких цен. Чтобы реализовать этот проект, К2 должна вложить в открытие нового филиала около 2 млн: эти деньги она рассчитывает окупить за три года, и, таким образом, среднемесячные вложения составляют около 55 тыс. рублей.

У К1 есть два ответных варианта: договориться с арендодателем и снять его помещение за 150 тыс., чтобы не въехала К2, или не договариваться.

Предположим, обе компании готовы помещение арендовать. Тогда К1, как сосед, получит преимущественное право аренды. При этом, если К1 снимает дополнительное помещение, и К2 в него не въезжает, то убытки К1 равны арендной плате 150 тыс. в месяц, а К2 убытков не несет. Если К2 въезжает, то часть клиентов К1 переходит к конкуренту. В результате К1 теряет около 220 тыс. прибыли, а К2 получает небольшой объем прибыли в размере около 70 тыс. в месяц (не забудем, что из выручки в 220 тыс. большая часть, 150 тыс., будет уходить на оплату аренды).

Но при этом К1 может снизить цены, и тогда К2 лишится своего основного конкурентного преимущества. Если K1 снизит цены до уровня К2, то ее прибыль уменьшится при текущих объемах в среднем на 35 тыс. рублей, и ее убытки в целом составят 255 тыс. Однако, тогда К1 сохранит большую часть своих клиентов, и ее конкурент тоже понесет убытки. С учетом инвестиций в открытие нового филиала и ежемесячных расходов на аренду помещения минимальные потери К2 составят 100 тыс. в месяц.

Представим последовательность действий игроков в виде дерева, вершины веток которого показывают выигрыш каждой компании. Это представление характерно для игр в расширенной форме, каждая ветка соответствует действию, которое может выбрать каждый игрок. В качестве выигрыша договоримся считать ежемесячную прибыль / убыток компаний.

Изменение прибыли К1 отмечено красным цветом, выигрыш К2 – синим. Исходная точка, показанная в левой части рисунка – это начало игры для К1. Игра является последовательной, то есть каждая компания реагирует на предыдущий шаг конкурента.

Последовательность действий двух компаний

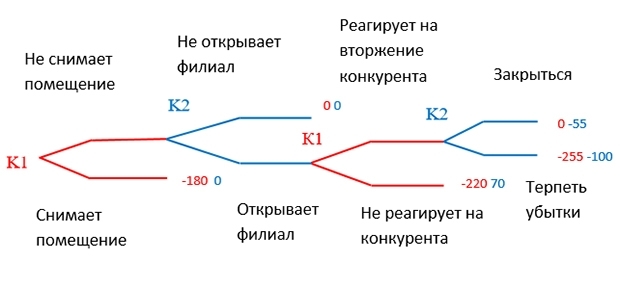
Воспользуемся методом обратной индукции для поиска оптимальной стратегии. Суть метода заключается в решении игры с конца. Последний ход в игре остается за K2: сравниваем ее выигрыши, отмеченные синим цветом: -55 и -100. Убыток в 55 тыс. руб. – лучше, чем в 100 тыс. Поэтому, если конкурент будет вести себя агрессивно, K2 выгоднее эту торговую точку закрыть.

Следующий с конца ход принадлежит K1. Если она временно опускает цены до уровня конкурента, то с финансовой точки зрения ничего не зарабатывает и не теряет: результат 0. Если же вообще никак не реагирует на вторжение конкурента на свою рыночную территорию, то ежемесячные убытки достигают 220 тыс. руб. Поэтому, К1 выгоднее на действия К2 реагировать.

Далее ход К2: открывать или не открывать филиал? Если открывать, то ежемесячно придется списывать по 55 тыс. руб. (сумму ежемесячных инвестиций). А если филиал не открывать, то выигрыш будет равен 0.

Наконец, наступает ход K1: снимать или нет дополнительное помещение? Ответ: не снимать. Так как убытки от аренды составят 150 тыс. рублей в месяц. А другой вариант действий позволяет свести потери к 0.

Таким образом, когда решаешь условия игры с конца, становится понятным, что К1 наиболее выгодно активно ответить на действия конкурента, но при этом не имеет смысла снимать соседнее помещение. А К2, с учетом агрессивного ответа К1, вообще не стоит открывать филиал. Однако такие выводы логично напрашиваются только в том случае, если соперники могут предположить выигрыш друг друга при различном развитии событий.

Данная игра была воплощена в жизнь одной из компаний Воронежа, работающей в сфере оптики и выступившей в роли К1. После того, как на региональный рынок попыталась войти федеральная компания K2, воронежские салоны в течение трех месяцев держали низкие цены на контактные линзы. В результате федеральная сеть, не получив искомой прибыли, закрыла свое подразделение в городе.

Плюсы и минусы метода

В теории игр есть несколько проблемных мест:

• Не всегда можно предсказать выигрыш.
• Игроки могут не придерживаться правильной стратегии, а играть хаотично или по принципу «уничтожить противника». Это стратегия, которую Роберт Аксерольд назвал бы «завистливой».
• Любой игрок может рассмотреть варианты, не включенные конкурентом в дерево стратегий.

Основное преимущество теории игр в бизнесе – возможность представить проблему с точки зрения конкурентов. Зная затраты конкурента, его основную стратегию и варианты действий, можно получить мощное преимущество в конфликте интересов и на рынке в целом.

Источник: www.e-xecutive.ru