Еще один тип заданий №15 Профильного ЕГЭ по математике — это задачи на нахождение точек максимума и минимума функций, а также их наибольших или наименьших значений. Многие из них решаются с помощью производной.
Такие задачи есть и в экономике. Например, максимизация прибыли или оптимизация издержек бизнеса — и многие другие.
1. Строительство нового завода стоит 78 млн рублей. Затраты на производство x тысяч единиц продукции на таком заводе равны млн рублей в год. Если продукцию завода продавать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более, чем за 3 года?
Чтобы прибыль за три года была не меньше 78 млн рублей, необходимо, чтобы каждый год прибыль была не меньше 26 млн рублей. Это значит, что должно выполняться неравенство:
Здесь — прибыль за год. Рассмотрим функцию
6–Я МЕЖДУНАРОДНАЯ ОНЛАЙН–КОНФЕРЕНЦИЯ «ПРОФЕССИОНАЛОВСАДОВОГО РЫНКА»
Наибольшее значение этой функции должно быть не меньше, чем 26.
Графиком функции является парабола с ветвями вниз. Наибольшее значение функции достигается при , то есть в вершине параболы.
или . Поскольку , получим: Тогда
2. Зависимость объема Q (в штуках) купленного у фирмы товара от цены Р (в рублях за штуку) выражается формулой , где . Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q + 5000000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство.
Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Будем рассматривать прибыль как функцию от цены продукции. Так как прибыль, по условию, равна разности дохода от продажи товара и затрат на его производство, получим:

Обратите внимание, что можно записывать 1000 как , 1000000 как . Работать со степенями проще, чем с длинными рядами нулей.

После того как фирма уменьшила первоначальную цену на 20%, ее прибыль не изменилась. Значит,
Приравняем эти величины.
Разделим обе части уравнения на
Значит, первоначальная цена продукции равна 10 тысяч рублей за штуку. После снижения на 20% цена за штуку стала равна 8 тысяч рублей.
На сколько же процентов следует увеличить сниженную цену, чтобы прибыль была наибольшей? И при каком значении цены получается наибольшая прибыль?
Другими словами, мы находим наибольшее значение функции
Эта функция задает квадратичную параболу с ветвями вниз. Можно найти ее точку максимума с помощью производной. Или просто найти координату вершины параболы:
Остается решить стандартную задачу на проценты. На сколько процентов надо увеличить 8000, чтобы получить 9000?
Офис Авито: спортзал, 15 этаж, капсулы для сна!
Теперь применение производной.
3. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет условных единиц. Если на втором объекте работает t человек, то их суточная зарплата составляет у. е. (условных единиц).
Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Обратите внимание, что в этой задаче переменная t — это не время! Переменная t здесь — некий параметр, через который выражены количество работающих на объекте человек и их суточная зарплата.
Сколько человек работает на каждом объекте? Мы не знаем. Нам надо найти, сколько должно быть рабочих на каждом объекте, чтобы затраты на оплату их труда оказались наименьшими.
Пусть на первом объекте работает х человек. Тогда на втором 24 —х человек, поскольку всего в бригаде 24 рабочих. Запишем данные задачи в таблицу:
| I объект | II объект |
| Количество рабочих | |
| Оплата |
Пусть функция — зависимость затрат на оплату труда рабочих от количества рабочих на первом объекте.
Найдем наименьшее значение функции Раскроем скобки в формуле функции:
Задачи на оптимизацию. Задание №17 из ЕГЭ
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t² тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
Решение
Пусть (y) — количество лет хранения акций, (x ) — количество лет держания вырученных от продажи акций средств в банке.
Имеем (x +y=20) , откуда (x=20-y) .
Запишем уравнение (целевую функцию) прибыли (y^2+y^2*x*0,25) , подставим выражение для (x) ,
имеем (y^2+y^2*(20-y)*0,25=y^2+5y^2-0,25y^3) .
Возьмем производную от полученного выражения, имеем (12y+0,75y^2) или (y=12:0,75=16) .
Таким образом, держать средства для получения максимальной прибыли следует 16 лет.
Ответ: 16.
Задача №2
Условие:
Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t 3 часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t 3 часов в неделю, они производят t приборов. За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?
Решение
Пусть (x ) — количество приборов, выпущенных на первом заводе, (y ) — количество приборов, выпущенных на втором заводе. Тогда (x+y=20) или выразим (y) имеем (y=20-x) .
Запишем целевую функцию (4x^3+у3= 4x^3+(20-x)^3=4x^3+8000-1200x+60x-x^3=3x^3-1140x+8000) .
Возьмем произодную от полученного выражения имеем (9x^2-1140=0) .
Решим полученное уравнение (x^2=126) .
Получаем, что на первом заводе следует выпустить 11 приборов. Соответственно, на втором заводе надо выпустить 9 приборов. Посчитаем наименьшую сумму, которую придется заплатить рабочим за неделю.
Имеем (1000*4*11^3+1000*9^3=1331000*4+729000=5324000+729000=6053000) .
Ответ: 6053000.
Задача №3
Условие:
Зависимость количества Q (в шт., 0 ≤ Q ≤ 20000) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q=20000-P. Затраты на производство Q единиц товара составляют 6000Q + 4000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0
Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Решение
Запишем целевую функцию, прибыль фирмы, она равна PQ-6000Q- 4000000-tQ.
Подставим в нее значение Q=20000-P.
Имеем P(20000-P)-6000(20000-P)-4000000-t(20000-P)=20000P-P 2 -120000000-6000P-4000000-20000t+tP=-P 2 +14000P+tP-20000t-124000000=-P 2 +P(14000+t)-(20000t+124000000).
По условию задачи эта функция достигает максимума, найдем точку максимума, для этого возьмем производную, приравняем нулю и решим полученное уравнение.
Имеем -2Р+14000+t=0, откуда получаем значение P=7000+t/2.
Подставим полученное значение в целевую функцию, имеем -(7000+t/2) 2 +(7000+t/2)(14000+t)- 20000t+124000000) = 49000000 + 7000t + t 2 /4+98000000+7000t+7000t+t 2 /2=3t 2 /4+21000t+147000000.
Найдем точку максимума, т. е. возьмем производную, приравняем ее нулю и решим полученное уравнение.
Имеем 1,5t+21000=0 или t=14000.
При этом значении сумма налогов полученных государством будет максимальна. Но у по условию задачи оно должно быть меньше 10000. Поэтому положим t=10000.
Ответ:10000.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Источник: myalfaschool.ru
Решение
В данной задаче предлагается вычислить норматив численности рабочих по соответствующим нормам выработки. Формула для этого следующая:
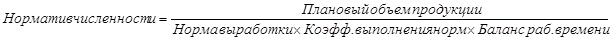
Подставляем:
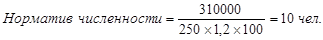
Пример 4. Количество рабочих мест продавцов-консультантов магазина «Электрика» равно 15. Магазин работает без перерыва с 9 до 19 часов (в субботу с 10 до 18 часов), выходной — воскресенье. Время на подготовку рабочего места — 20 минут в день. Продолжительность рабочей недели продавца — 40 часов. Полное число рабочих дней на одного работника в год — 256.
Эффективный фонд рабочего времени продавца-консультанта в год — 228 дней. Определите явочную и среднесписочную численность продавцов.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Об этом полезно знать:
II этап сестринского процесса: сестринская диагностика Как только медицинская сестра приступила к анализу полученных в ходе обследования данных.
Философское понятие свободы. Свобода и ответственность Категория: Ответы к вступительному экзамену по философии. Свобода — в самом общем смысле.
Государственные органы управления физической культурой и спортом В предыдущей главе пособия были представлены формы физической культуры и соответствующие виды физкультурно- спортивной деятельности.
Методы осуществления налоговой политики и управление налогообложением Параметры налоговой системы во многом зависят от проводимой государством налоговой политики.
Тема 2.1. Внутрибольничная инфекция. Лекция № 2 План лекции: 1. Масштаб проблемы ВБИ, структура ВБИ. 2. Способы передачи инфекции в медицинском учреждении. 3.
Источник: studopedia.ru
