Считается, что если отрезок разделить на части таким образом, что меньшая его часть будет относиться к большей, как бОльшая – к целому отрезку, то такое разделение дает пропорцию 1/1,618, которую древние греки, позаимствовав ее у еще более древних египтян, назвали «золотым сечением». И что многие архитектурные сооружения – соотношения контуров строений, соотношение между их ключевыми элементами — начиная с египетских пирамид и кончая теоретическими построениями Ле Корбюзье — основывались на этой пропорции.
Ей же соответствуют числа Фибоначчи, спираль которого дает развернутую геометрическую иллюстрацию этой пропорции.
Более того, размеры человеческого тела (от подошв до пупка, от пупка до головы, от головы до пальцев поднятой руки), начиная от идеальных пропорций, увиденных в Средневековье (витрувианский человек и проч.), и кончая антропометрическими измерения населения СССР, довольно-таки близки к этой пропорции.
А если добавить, что подобные фигуры обнаружены в совершенно разнородных биологических объектах: раковинах моллюсков, расположении семян в подсолнухе и в кедровых шишках, то понятно почему иррациональное число, начинающееся как 1,618 объявлялось «божественным» — его следы прослеживаются даже в форме галактик, тяготеющих к спирали Фибоначчи!
С учетом всех перечисленных примеров, можно предполагать:
- мы имеем дело с поистине «большими данными»,
- даже в первом приближении они указывают на некую, если не всеобщность, то необыкновенно широкое распространение «золотого сечения» и близких к нему значений.
В экономике
Широко известны и интенсивно используется диаграммы Лоренца для визуализации доходов населения. Эти мощный макроэкономический инструмент с разнообразными вариациями и уточнениями (децильный коэффициент, индекс Джини) используются в статистике для социально-экономического сопоставления стран и их особенностей и могут быть обоснованием для принятия больших политических и бюджетных решений в области налогообложения, здравоохранения, выработки планов развития стран и регионов.
И хотя в нормальном бытовом сознании доходы и расходы связаны между собой накрепко, в Гугле это не так… Поразительно, но найти связь диаграмм Лоренца с распределением расходов мне удалось только у двух российских авторов (буду признателен, если кто-то знает подобные работы как в русском, так и англоязычном секторе интернета).
Первая — диссертация Т. М. Буевой. Диссертация была посвящена, в частности, оптимизации расходов на марийских птицефабриках.
Другой автор, В.В. Матохин (взаимные ссылки авторов имеются), подходит к делу более масштабно. Матохин, физик по исходному образованию, занимается статистической обработкой данных, используемых при принятии управленческих решений, а также оценкой адаптивности и управляемости компаний.
Концепция и примеры, приводимые ниже, почерпнуты из работ В. Матохина и его коллег (Матохин, 1995), (Antoniou и др., 2002), (Крянев, и др., 1998), (Матохин и др. 2018). В связи с этим следует добавить, что возможные ошибки в интерпретации их работ являются исключительной собственностью автора этих строк и не могут быть приписаны исходным академическим текстам.
Неожиданное постоянство
Отраженное на ниже представленных графиках.
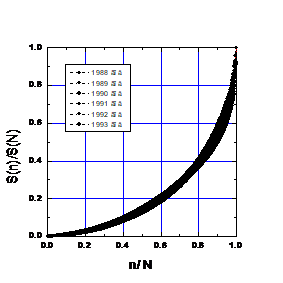
1. Распределение грантов по конкурсу научно-технических работ по Государственной программе “Высокотемпературная сверхпроводимость”. (Матохин, 1995)
Рис.1. Пропорции в ежегодном распределении средств по проектам в 1988-1994 гг..
Основные характеристики ежегодных распределений приведены в Табл.3, где SN — ежегодная сумма распределяемых средств (в млн. руб.), а N — число финансируемых проектов. С учетом того, что за эти годы менялся персональный состав жюри конкурса, бюджет конкурса и даже масштаб денег (до реформы 1991-го года и после), стабильность реальных кривых во времени поразительна. Черная полоса на графике составлена из экспериментальных точек.
| 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | ||
| S | 273 | 362 | 432 | 553 | 345 | 353 | 253 | X |
| Sn | 143.1 | 137.6 | 136.9 | 411.2 | 109.4 | 920 | 977 | Y |

2. Кривая расходов, связанных с продажами товарных запасов (Котляр, 1989)
Рис.2
3. Тарифная сетка жалований чинам
В качестве примера для построения диаграммы взяты данные из документа «Ведомость: сколько каким чинам по штатам обыкновенного годового жалования в год иметь положено» (Суворов, 2014)(«Наука побеждать»).
| Чин | Жалование (руб.) |
| Полковник | 585 |
| Подполковник | 351 |
| Майор Пример | 292 |
| Майор Секунд | 243 |
| Квартермистр | 117 |
| Адъютант | 117 |
| Комиссар | 98 |
| . | . |

4. Осредненный рабочий график американского менеджера среднего звена (Mintzberg, 1973)
Рис.4
Приведенные нормированные графики позволяют предполагать, что в иллюстрируемых ими хозяйственных активностях имеется общая закономерность. При радикальном различии по конкретике хозяйственной деятельности, по ее месту и времени, весьма вероятно, что сходство графиков продиктовано неким фундаментальным условием функционирования экономических систем.
Не иначе, как за тысячелетия ведения хозяйственной деятельности на основании огромного числа проб и ошибок субъекты этой деятельности нащупали некоторую оптимальную стратегию распределения ресурсов. И интуитивно используют ее в текущей деятельности. Такое предположение хорошо согласуется с известным принципом Парето: 20% наших усилий дают 80% результатов. Здесь явно наблюдается нечто подобное. Приведенные графики выражают эмпирическую закономерность, которая в случае преобразования в диаграмму Лоренца с достаточной точностью описывается при показателе степени «альфа» равном 2. При этом показателе диаграмма Лоренца превращается в часть окружности.
Можно назвать эту, еще не имеющую устойчивого наименования характеристику, выживаемостью. По аналогии с выживаемостью в дикой природе, выживаемость хозяйственной системы определяется ее наработанным приспособлением к условиям социально-экономической среды и способностью адаптироваться к изменениям рыночных условий.
Это значит, что система, в которой распределение расходов близко к идеальному (при показателе степени «альфа», равном 2, или распределением расходов «по окружности»), имеет наибольшие шансы сохраниться в существующем виде. Примечательно, что в ряде случаев такое распределение определяет и наибольшую рентабельность предприятия. Например, здесь. Чем меньше коэффициент отклонения от идеального, тем выше рентабельность предприятия (Буева, 2002).
| Наименование хозяйства, района | Рентабель-ность (%) | Коэффициент отклонения | |
| 1 | ГУП п/ф «Волжская» Волжского р-она | 13,0 | 0,336 |
| 2 | СПК п/ф «Горномарийская» | 11,1 | 0,18 |
| 3 | УМСП с-з «Звениговский» | 33,7 | 0,068 |
| 4 | ЗАО «Марийское» Медведевского р-на | 7,5 | 0,195 |
| 5 | ОАО «Тепличное» Медведевского р-на | 16,3 | 0,107 |
| . | |||
| 47 | СПК (к-з) «Рассвет» Советского р-она | 3,2 | 0,303 |
| 48 | С-з «Броневик» Килемарского р-она | 14,2 | 0,117 |
| 49 | СПК СХА «Авангард» Моркинского р-она | 6,5 | 0,261 |
| 50 | СХА к-з им. Петрова Моркинского р-она | 22,5 | 0,135 |
Практические выводы
Планируя расходы, как компании, так и домохозяйства, полезно построить по ним кривую Лоренца и сверить ее с идеальной. Чем ближе ваша диаграмма будет к идеальной, тем вероятнее, что планируете правильно и что ваша деятельность будет успешна. Такая близость подтверждает, что ваши планы близки к опыту хозяйственной деятельности человечества, отложившемся в таких общепризнанным эмпирических закономерностях, как принцип Парето.
Однако можно предположить, что здесь речь идет о функционировании зрелой хозяйственной системы, ориентированной на рентабельность. Если же речь не идет о максимизации прибыли, а, например, о задаче модернизации компании или о принципиальном увеличении ее доли рынка, ваша кривая распределения расходов будет отходить от окружности.
Понятно, что и в случае старт-апа с его специфической экономикой диаграмма Лоренца, отвечающая наибольшей вероятности успеха, будет также отклоняться от окружности. Можно высказать гипотезу, что отклонения кривой распределения расходов внутрь окружности соответствует как повышенным рискам, так и пониженной адаптивности компании. Однако без опоры на большие статистические массивы по старт-апам (как успешным, так и неуспешным) обоснованные квалифицированные прогнозы вряд ли возможны.
По другой гипотезе, отклонение кривой распределения расходов от окружности наружу, может быть сигналом как чрезмерной зарегулированности управления, так и сигналом надвигающегося банкротства. Для проверки этой гипотезы так же необходима определенная эталонная база, которая, как и в случае старт-апов, вряд ли существует в открытом доступе.
Вместо заключения
Первые большие публикации по этой тематике датируются 1995 годом (Матохин, 1995). И малоизвестность этих работ при их универсальности и радикально новом использовании широко применяемых экономистами моделей и инструментов остается в некотором смысле загадкой…
- Диаграмма Лоренца
- распределение расходов
- рентабельность
- экономика
- спираль Фибоначчи
- стар-апы
- рынок
- доля рынка
Источник: habr.com
Принцип Парето и Золотое сечение
В современной экономике для управления крупными, средними и мелкими предприятиями большинством руководителей принято использовать эмпирическое правило, открытое в 1877 году и названное в честь экономиста и социолога Вильфредо Парето («Принцип Парето» или «Принцип 20/80»). Оно применяется при анализе факторов эффективности деятельности организаций и оптимизации их результатов. В общем виде это правило звучит как «20% усилий дают 80% результата, а остальные 80% усилий – лишь 20% результата». Таким образом, правильно выбрав минимум приоритетных действий, можно получить большую часть запланированного результата, не задействовав при этом всех усилий [1].
Наряду с принципом Парето для поиска оптимального набора прикладываемых усилий применяется принцип «Золотого сечения», который позволяет решить следующую задачу: «в каком соотношении выделить в составе целого некоторые две части так, чтобы они отвечали бы условиям структурной и функциональной целостности и устойчивости единства с внешней средой». Красивый ответ на поставленную задачу дал Леонардо да Винчи в 1509 г, сформулировав правило «Золотого сечения», которое гласит: «Золотое сечение – это такое пропорциональное деление отрезка на две неравные части, при котором длина отрезка так относится к большей части, как большая часть относится к меньшей» [2].
Гармонизация уместна там, где есть структурное разнообразие. «Золотое сечение» можно рассматривать в качестве опорного отношения для гармонизации экономики организаций, состоящих из различных подразделений. Оптимальное (гармонизованное) разнообразие, которое при этом обеспечивается и гарантирует их системное качество, а, следовательно, функциональную эффективность, в результате которой сводится к минимизации непродуктивных (непроизводительных) издержек. Законы Меры, Гармонии, «Золотого сечения» дают возможность строить экономику, суть которой – оптимальное (гармоничное) распределение ресурса [3].
Понятия Меры, Гармонии, «Золотое сечение» пронизывают всю историю науки и культуры. Пирамида Хеопса (Хуфу), самая известная из египетских пирамид, знаменитый Парфенон – храм Афины Парфенос на Акрополе в Афинах, храм Агии Софии в Константинополе, непревзойденная «Джоконда» Леонардо Да Винчи, картины Рафаэля, поэзия А.С. Пушкина и М.Ю. Лермонтова, этюды Шопена, музыка Бетховена и Чайковского, «Модулор» Ле Корбюзье, творения древнерусского зодчества – храм Покрова на Нерли, церковь Вознесения в селе Коломенском – вот не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией, основанной на «Золотом сечении» [4].
Так и в данной работе для исследования мы используем принцип «Золотого сечения», математическая формулировка которого представляется следующим образом:
c :b = b :a, при a + b = c (1)
Графически «Золотое сечение» выглядит как пропорциональное деление отрезка на две неравные части, при котором весь отрезок так относится к большей части, как большая к меньшей (c : b= b : a= 1,618):
Рис.1. Золотое сечение
Известно, что в 1202 г. итальянский математик Леонардо Пизанский, больше известный как Фибоначчи, вывел последовательность чисел, в которой последующее число равно сумме двух предыдущих чисел: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55 и т.д., позднее эта последовательность получила название ряда Фибоначчи [5].
Также Ф = 1,618 является положительным корнем уравнения:
Для обобщенного варианта Золотых р-сечений, предложенного А.П. Стаховым и И.В. Витенько, выведена пропорция:
с : b= (3)
Тогда обобщенное уравнение для Золотых р-сечений выглядит следующим образом:
Корнями уравнений для Золотых р-сечений при определенных значениях параметра р будут [6]:
Значения корней уравнения для Золотыхр-сечений при разных параметрах р представлены ниже (рис.2) [6]:
р= 4 = 1, 324
р= 5 = 1, 285
р= 6 = 1, 255
р= 7 = 1, 232
Рис.2 Золотые р-сечения
Следует отметить, что формула для нахождения корня в уравнениях Золотых р-сечений порождает формулу, которая задает бесконечное количество определенных последовательностей, подобных числам Фибоначчи [7]:
Тогда обобщенные числа Фибоначчи будут иметь следующий вид (таб.1):
Обобщенные числа Фибоначчи
Источник: be5.biz
Леонардо да Винчи, золотое сечение и маркетинг – рассказываем про взаимосвязь, которая помогает продавать товары и услуги

Связаны ли маркетинг и симметрия? Имеют ли значение для рекламы пропорции изображений, расположения символов, подбора цветовой гаммы? Помогают ли они лучше продавать продукт и привлекать покупателей? Да, и еще раз да! И лучшие дизайнеры, маркетологи и архитекторы руководствуются в своей работе принципом золотого сечения.
Да что говорить, сама Матушка-Природа его «уважает», придавая своим творениям соответствующую этому закону форму (растения, животные, ураганы, даже Галактики).
Откуда взялся термин «золотое сечение»
Золотое сечение пришло в маркетинг из средневековых трактатов, хотя саму его суть заметили и поняли еще древние египтяне, используя его, в том числе для строительства Великих пирамид. И неудивительно, ведь гармоничность и правильность пропорций увлекали лучшие умы человечества и многие века назад.
Однако понятие «золотого сечения» больше всего связывают с именем знаменитого математика Фибоначчи и гениального живописца, скульптора и исследователя Леонардо да Винчи. Последнему и принадлежит название, которое закрепилось во всех отраслях деятельности человека, включая маркетинг.
К примеру, «Мона Лиза» нарисована по канонам «золотого сечения», как и «Тайная Вечеря», «Венера» Боттичелли, «Святое семейство» Микеланджело или «Сикстинская Мадонна» Рафаэля Санти. Творения наших русских живописцев – Андрея Рублева, А. Иванова, Н. Ге, И. Левитана – оттого радуют глаз, что очень гармоничны и пропорциональны.
Золотое сечение – это (без сложных математических объяснений)
Золотое сечение построено на соотношении целого и его частей, где количественные пропорции между двумя подсистемами должны находиться в пропорции 0,62:0,38 (или 1,618:1,00). 1.68 еще называют «число Фи». Если говорить о геометрии, то длинная часть отрезка соотносится с короткой так же, как весь отрезок соотносится с длинной его частью.
Форма, которая построена на сочетании симметрии и золотого сечения, лучше зрительно воспринимается, она способствует появлению ощущения красоты и гармонии. Лучшие маркетологи и дизайнеры давно это учитывают и активно используют при разработке макетов, дизайн-проектов, планов и пр. Так что пользователи, покупатели и клиенты встречаются с золотым сечением повсеместно.

В какие сайты, символы и логотипы влюбляются клиенты
Вы даже не сможете объяснить себе, почему вам так нравится сайт National Geographic или логотип «Пепси». А все потому, что они базируются на «золотых пропорциях». Именно на них вы подсознательно обращаете внимание, и именно они «отпечатываются» в вашей памяти. Изучая журнал, вы бегло листаете страницы, но какой-то заголовок вдруг привлекает взгляд. И все потому, что картинка, элементы на ней, цветовая палитра и заголовок вписываются в лекала «золотого сечения».
Золотое сечение в руках умелых маркетологов
Правило золотого сечения грамотно используют дизайнеры, колористы и маркетологи, когда подбирают цветовую гамму для продукта, ведь это тот самый стандарт, который гарантировано дает свои плоды. И по сей день оно считается каноном построения композиции. А логотип, товарный знак, упаковка, да вся айдентика – такая же композиция, при создании которой нужно учитывать нормы и правила. И сейчас, когда внимание пресыщенного и избалованного потребителя завоевать так сложно, любые маневры и хитрости особенно необходимы.
Расположение элементов рекламного изображения по «золотому сечению» акцентирует внимание на первостепенных компонентах и деталях, выводит на первый план то, что должно доминировать, вызывает положительные эмоции у потенциального покупателя.
Рекламный мир знает массу примеров применения «золотого сечения» у очень популярных брендов и компаний. Логотип Toyota, Twitter, Apple, Pepsi, British Petroleum – все взывают к нашему чувству гармонии, поскольку на их восприятие работает «золотое сечение».

Золотое сечение в выборе цвета для рекламной продукции
Не менее актуален принцип золотого сечения и для подбора цветового решения в рекламе. Приоритетный цвет и остальные используются в пропорции 1.618:1. Это не раздражает глаз, делает восприятие всей цветовой палитры комфортным, обеспечивает хорошее запоминание при условии, что цвета скомпонованы и подобраны должным образом.
На 100 % работает золотое сечение и при составлении рекламных текстов, плакатов, объявлений и предложений (на любых POS-материалах). Очень важно, чтобы человек не отбросил вашу листовку, а заинтересовался ею. Так что стоит прибегнуть к определению пропорций размера самого текста, его отдельных частей и заголовка.
Если, к примеру, шрифт имеет размер 12, то заголовок (12*1.618=19.4) должен быть 19-го размера. Точно также располагайте отдельные элементы на POS-материале – где главный элемент соотносится со второстепенным также, как вся листовка с главным элементом. И действуем аналогично по отношению к каждой части.
Математика, геометрия и искусство продавать
Маркетинг активно пользуется достижениями других наук, и золотое сечение – тому верное доказательство. Точно также все специалисты «Ритейл Навигатор» в своей деятельности для заказчика применяют все самое эффективное и полезное для продаж – включая золотое сечение. Это один из наших секретов, а узнать больше вы можете на сайте – ссылка в описании канала.
Источник: retail-navigator.ru
