Таким образом, если кредит взят на (n) лет, то это значит, что сумму кредита (A) разделили на (n) равных частей и что каждый год после платежа сумма долга уменьшается на (dfrac1n A) по сравнению с долгом на начало года.
Пример: Александр взял в банке кредит на (50,000) рублей на (3) месяца, причем выплачивать кредит он должен ежемесячными выплатами так, чтобы сумма долга каждый месяц уменьшалась на одну и ту же величину. Сколько рублей составит переплата Александра по кредиту, если процентная ставка в банке (10%) ?
Т.к. кредит взят на (3) месяца, то после первой выплаты долг должен составить (A-frac13A=frac23 A) , после второй (frac23A-frac13A=frac13A) , а после третьей — (frac13A-frac13A=0) рублей. Составим таблицу, производя все вычисления в тыс. рублей: [begin <|l|c|c|c|c|>hline texttexttext\ text%\ hline 150+0,1cdot 500,1cdot 50+frac13cdot 50\ hline 2frac23cdot 50+0,1cdotfrac23cdot 500,1cdot frac23cdot 50+frac13cdot50\ hline 3frac13cdot 50+0,1cdot frac13cdot 500,1cdot frac13cdot 50+frac13cdot 50\ hline end]
15 задание ЕГЭ математика профиль
Таким образом, всего Александр заплатил банку (big(0,1cdot 50+dfrac13cdot 50big)+big(0,1cdot dfrac23cdot 50+dfrac13cdot50big)+big(0,1cdot dfrac13cdot 50+dfrac13cdot 50big)) тыс.рублей.
Перегруппируем слагаемые и вынесем за скобки общие множители:
(0,1cdot 50 left(1+dfrac23+dfrac13right)+3cdot dfrac13cdot 50=0,1cdot 50cdot 2+50)
Для того, чтобы найти переплату по кредиту, необходимо из того, что он в итоге заплатил банку, отнять сумму кредита:
(big(0,1cdot 50cdot 2+50big)-50=10) тыс. рублей.
Таким образом, его переплата составила (10,000) рублей.
I. что каждая выплата состоит из двух частей:
первая часть — это сумма “набежавших” процентов на текущий долг (в первый год это (0,1cdot 50) , во второй — (0,1cdot big(frac23cdot 50big)) и т.д.)
вторая часть всегда фиксирована — это та часть, на которую должен уменьшаться долг каждый год (в нашем примере это (frac13cdot 50) ).
Действительно, когда клиент выплачивает “набежавшие” проценты, сумма его долга становится равна той, которая была до начисления процентов (например, в первый год становится равна (A) ). А далее он еще вносит (frac 1n) часть от этого долга. И таким образом сумма долга уменьшается на (frac 1n) часть, что и подразумевает дифференцированная система платежей.
II. переплата по кредиту всегда равна сумме “набежавших” процентов на долг в первый год, во второй год, в третий год и т.д.
В нашем примере переплата как раз равна (0,1cdot 50+0,1cdot frac23cdot 50+0,1cdot frac13cdot 50) .
Формула для выплаты в (i) -ый год: [<Largecdot dfracA+dfrac1n A>>] где (n) – количество лет, на которое взят кредит, (A) – сумма кредита, (r%) – процентная ставка.
Задание 15 #3893
Уровень задания: Равен ЕГЭ
15 января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
Задача № 15 ЕГЭ по математике. Вклады, кредиты. Часть 3.
— 1-ого числа каждого месяца долг возрастает на (r%) по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на (13%) больше, чем сумма, взятая в кредит. Найдите (r) .
Фраза “15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца” означает, что кредит будет выплачиваться дифференцированными платежами. Следовательно, можно составить таблицу, взяв за (A) сумму кредита: [begin <|c|c|c|c|>hline text text % A frac1A+frac rA\ hline 2 fracA+frac rcdot fracA . . \ hline 25 frac1A+frac rcdot frac1A
– с февраля по июнь каждого года необходимо выплачивать часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите общую сумму выплат по такому кредиту, если он был взят на 4 года.
Из условия следует, что платежи дифференцированные. Следовательно, каждый платеж состоит из двух частей:
1) первая часть – это (dfrac14cdot 3) (млн. рублей), так как кредит взят на 4 года;
2) вторая часть в (n) -ый год – это “набежавшие проценты” на долг в (n) -ый год, то есть в первый год это (0,1cdot 3) (млн. руб.), во второй – это (0,1cdot frac34cdot 3) (млн. руб.), в третий год это (0,1cdot frac24cdot 3) (млн. руб.), в четвертый – это (0,1cdot frac14cdot 3) (млн. руб.).
Таким образом, общая сумма выплат равна сумме платежей и равна [begin =4cdot dfrac14cdot 3+0,1cdot 3cdot left(1+dfrac34+dfrac24+dfrac14right)=3+0,75=3,75end]
Задание 17 #2022
Уровень задания: Равен ЕГЭ
Под какое наибольшее количество процентов годовых должен быть выдан кредит в банке сроком на 7 лет, чтобы переплата по такому кредиту составляла не более (56%) от суммы кредита, а погашение кредита происходило ежегодными платежами так, чтобы долг каждый год уменьшался равномерно?
Заметим, что фраза “долг уменьшался равномерно” означает, что выплаты происходят с помощью дифференцированных платежей.
Пусть в кредит было взято (A) рублей. Пусть также (y%) – годовая ставка в банке. Тогда в первый год после начисления процентов долг увеличится на (frac ycdot A=0,01ycdot A) рублей, во второй — на (fraccdot frac67cdot A=0,01ycdot frac67cdot A) рублей и т.д. Составим таблицу:
[<large< begin <|l|c|c|c|>hline text text text% text \[3pt] hline 1 0,01ycdot A+frac17cdot A frac67cdot A+0,01ycdotfrac67cdot A frac57cdot A\[3pt] hline 3 0,01ycdotfrac57cdot A+frac17cdot A frac47cdot A+0,01ycdotfrac47cdot A frac37cdot A\[3pt] hline 5 0,01ycdotfrac37cdot A+frac17cdot A frac27cdot A+0,01ycdotfrac27cdot A frac17cdot A\[3pt] hline 7 0,01ycdotfrac17cdot A+frac17cdot A >]
Таким образом, переплата (сумма всех платежей за вычетом суммы кредита) по кредиту составила
[R=0,01ycdot Acdot left(1+dfrac67+dfrac57+dfrac47+dfrac37+dfrac27+dfrac17right)=0,04ycdot A]
Т.к. переплата не должна превышать (56%) от суммы кредита, то (Rleqslant 0,56A) . Таким образом, имеем следующее неравенство:
[0,04ycdot Aleqslant 0,56A quad Leftrightarrow quad yleqslant 14]
Таким образом, наибольшая годовая ставка — это (y=14%) .
Задание 18 #1198
Уровень задания: Равен ЕГЭ
Константин решил взять в одном из двух банков кредит на покупку машины при условии, что он будет выплачивать кредит дифференцированными платежами. Первый банк предлагает Константину кредит на (6) лет с (frac%) годовых, а второй банк – на (5) лет с (12,5%) годовых. В каком банке ему выгодней взять кредит и сколько процентов от стоимости машины составляет эта выгода?
Составим таблицу для обоих банков, обозначив за (A) руб. сумму кредита.
Найдем сумму, которую составит переплата в этом случае: [dfracA+dfraccdot dfracA+ cdots +dfraccdot dfracA=0,16A quad text16%text< от стоимости машины>]
Найдем сумму, которую составит переплата в этом случае: [dfracA+dfraccdot dfracA+ cdots +dfraccdot dfracA=0,375Aquad text37,5% text< от стоимости машины>]
Таким образом, Константину выгоднее взять кредит в первом банке и выгода при этом составит (37,5%-16%=21,5%) .
Задание 19 #2020
Уровень задания: Равен ЕГЭ
В феврале 2015 года Аркадий Петрович взял кредит в банке под (13%) годовых, причем выплатить кредит он должен восемью платежами, вносимыми раз в год на счет после начисления процентов на оставшуюся сумму долга. Долг при этом должен уменьшаться каждый год равномерно. Сколько рублей составит переплата по кредиту, если больший платеж на (91,000) рублей больше меньшего платежа?
Фраза “долг при этом должен уменьшаться каждый год равномерно” означает, что кредит будет выплачиваться дифференцированными платежами.
Пусть Аркадий Петрович взял в банке (A) рублей. Т.к. кредит должен быть выплачен восемью платежами, то он взят на 8 лет. Составим таблицу:
[<large< begin <|l|c|c|c|>hline text text text% text \[3pt] hline 1 0,13cdot A+frac18cdot A frac78cdot A+0,13cdotfrac78cdot A frac68cdot A\[3pt] hline 3 0,13cdotfrac68cdot A+frac18cdot A frac58cdot A+0,13cdotfrac58cdot A frac48cdot A\[3pt] hline 5 0,13cdotfrac48cdot A+frac18cdot A frac38cdot A+0,13cdotfrac38cdot A frac28cdot A\[3pt] hline 7 0,13cdotfrac28cdot A+frac18cdot A frac18cdot A+0,13cdotfrac18cdot A 0\[3pt] hline end>>]
Заметим, что все платежи состоят из двух частей: вторая часть одинакова (left(frac18cdot Aright)) , а первая часть меняется, причем в первом платеже первая часть – наибольшая, а в последнем – наименьшая. Значит и первый платеж – наибольший, а последний – наименьший. Таким образом, получаем следующее уравнение:
(left(0,13cdot A+frac18cdot Aright)-left(0,13cdotfrac18cdot A+frac18cdot Aright)=91,000 quad Leftrightarrow quad 0,13cdot Aleft(1-frac18right)=91,000 quad Leftrightarrow)
(Leftrightarrow quad A=800,000)
Тогда переплата по кредиту равна сумме всех платежей за вычетом суммы кредита:
Источник: shkolkovo.net
Предприниматель 15 мая обратился в банк с просьбой о представлении кредита. В таблице представлен график его погашения. Текущий долг выражается в процентах от кредита.В конце каждого месяца, начиная с мая, текущий долг увеличивается на 5%, а выплаты по погашению кредита должны происходить с 1 по 14 число каждого месяца, начиная с июня. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Предприниматель 15 мая обратился в банк с просьбой о представлении кредита. В таблице представлен график его погашения. Текущий долг выражается в процентах от кредита.В конце каждого месяца, начиная с мая, текущий долг увеличивается на 5%, а выплаты по погашению кредита должны происходить с 1 по 14 число каждого месяца, начиная с июня. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Предварительный просмотр









Библиотека Ирины Эланс, основана как общедоступная библиотека в интернете. Онлайн-библиотеке академических ресурсов от Ирины Эланс доверяют студенты со всей России.
Библиотека Ирины Эланс
Полное или частичное копирование материалов разрешается только с указанием активной ссылки на сайт:
Ирина Эланс открыла библиотеку в 2007 году.
Источник: student-files.ru
15 января был выдан кредит на развитие бизнеса в таблице представлен график его погашения 5
Содержание:
- Плохо понимаете, как решать экономические задачи на дифференцированные платежи?
- Условие задачи
- Решение задачи
- Выводы
- Примеры условий реальных задач, встречающихся на ЕГЭ по математике
- Хотите разбираться в экономических задачах на дифференцированные платежи? Тогда жду вас на уроке!
Плохо понимаете, как решать экономические задачи на дифференцированные платежи?
Приветствую! Меня зовут Александр и мне 35+ лет. Я — профессиональный репетитор по математике, информатике и программированию. Двумя словами — я матерый технарь. Сфера моих интересов — исследование математических моделей, применяемых в задачах экономического блока, встречающихся на официальном экзамене ЕГЭ по математике.
Да, я прекрасно понимаю, что вы чрезвычайно занятой человек и имеете в настоящий момент кучу неотложных дел, но, несмотря на это, я все-таки рекомендую потратить $2$ минуты собственного времени и познакомиться с отзывами учеников, прошедших подготовку под моим началом.
Экономические задачи на дифференцированные платежи — очень популярный тип задач, которые дают решать на ЕГЭ по математике. Если вы плохо понимаете, что такое схема дифференцированных платежей, но хотите в этом разбираться на первоклассном уровне, то берите в руки телефон, набирайте мой контактный номер и записывайтесь на первый пробный урок.
Мои частные уроки проходят в различных территориальных форматах: дистанционно, на моей/вашей/нейтральной территории. Но в настоящий момент времени бешеную популярность имеет удаленный формат, посредством, например, программы «Скайп». И вам рекомендую остановиться именно на этом формате. $90%$ моих учеников предпочитают именно его. Это удобно, эффективно и недорого!
Условие задачи
В июле планируется взять кредит в банке на сумму $20$ миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
- Каждый январь долг возрастает на $30%$ по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась $47$ миллионов рублей?
Решение задачи
Как бы решал и анализировал эту задачу я. Во-первых, нужно определить, какой тип кредитования здесь применяется. Фундаментально типы можно разделить на $2$ следующих: платежи идут по дифференцированной схеме, и платежи происходят по аннуитетной схеме.
В приведенном условии присутствуют маркеры, которые позволяют однозначно определить, к какому типу кредитования относится эта задача. Давайте обратимся к следующей фразе: » В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года». Все встало на свои места! Перед нами экономическая задача на дифференцированные платежи.
Если для вас данная фраза не является информирующей, значит, вы плохо знакомы с математической моделью, свойствами и признаками дифференцированных платежей. Поэтому, во-вторых, я просто строго настаиваю на том, чтобы вы потратили необходимое количество времени и внимательнейшим образом познакомились с понятием дифференцированных платежей. Даже, если имеете какое-то представление, то повторение не станет лишним.
Давайте введем следующие обозначения:
| (S) — размер первоначального кредита | (r) — процентная ставка банка, выраженная в долях | (R = 1 + r) — для удобства расчетов |
| (n) — общее количество отчетных периодов | (i) — номер текущего отчетного периода | (%_) — размер начисленных банком процентов за конкретный период |
| (p_) — размер платежа за конкретный период | (P) — общая сумма всех выплат/платежей | (q) — ставка банка, выраженная в процентах |
Эти обозначения я использую практически в каждой экономической задаче на дифференцированные платежи. Это делает решения унифицированными и позволяет читателю переключаться между примерами, не теряя сути математических формул, за минимальное время.
Из условия вытекает, что:
| $S = 20$, млн. рублей | $q = 30%$ | $r = frac = frac = 0.3$ | $P = 47$, млн. рублей |
Кстати, сразу бросается в глаза бешеная процентная ставка банка! Она слишком оторвана от реальности. Адекватная кредитная банковская ставка находится в районе $12 — 18%$ годовых. Повторяю и буду повторять, что банковские займы — дело неправильное и их следует избегать.
Сейчас продемонстрирую решение, на которое мне потребовалось бы потратить не более $2$-х минут. Если бы я сдавал ЕГЭ по математике. Почему так быстро? Да потому, что здесь включается самая важная формула, которая выводилась нами, при построении математической модели дифференцированных платежей.
Кстати, вот эта формула: $P = frac + S$. Если не узнали ее, то это плохо. Нужно срочно изучать математическую модель, используемую в решениях экономических задач на дифференцированные платежи.
А ведь, что характерно, это будет единственная формула, которая нам потребуется для оптимального решения и получения молниеносного ответа. Разве нет? Ведь в этой зависимости нам известно все, кроме переменной $n$. А эта $n$ и есть ни что иное, как искомая величина, которая выражает количество отчетных периодов или общее время кредитования.
Подставляем известные в уравнение и получаем ответ!
$47 * 2 = 6 * (n + 1) + 20 * 2$
$6 * (n + 1) = 94 — 40$
Готово! Быстро? А то! Сложно? Нет, достаточно знать лишь одну математическую зависимость и уметь решать линейные уравнения.
То есть период кредитования должен составлять ровно $8$ лет, чтобы выполнились все требования и ограничения, указанные в постановке задачи.
Вроде получили ответ и все замечательно, но остается момент, связанный с тем, а правильный ли он? С высоченной вероятностью, что, да! Но я все-таки хочу провести доказательство правильности ответа через таблицу, сформированную в великолепной программе «MS Excel». Кстати, такие доказательные таблицы я получаю постоянно на своих частных уроках.
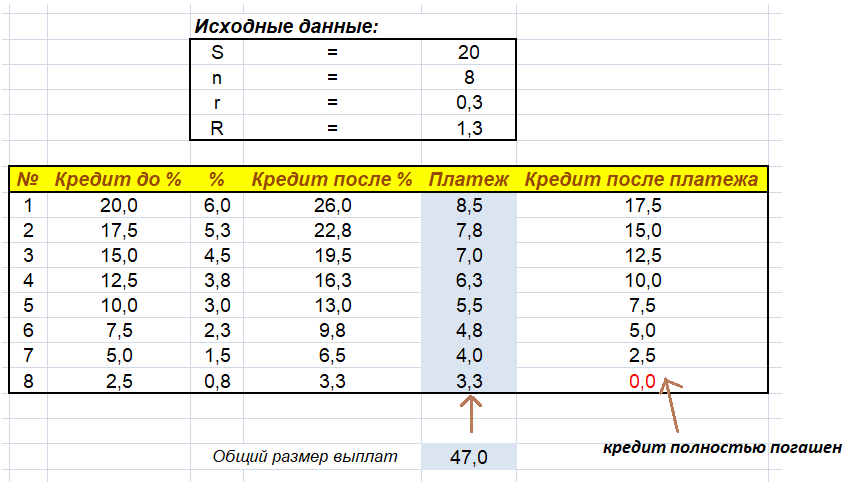
Данная таблица отражает все банковские операции, возникавшие в процессе кредитования. Ее структура очень наглядна. Четко прослеживается изменение тела взятой ссуды, также удобно анализировать размер платежа и размер начисляемых процентов. Всем рекомендую делать подобную верификацию полученного результата.
Ответ: 8.
Выводы
Пожалуй, можно сделать лишь один вывод: необходимо глубоко понимать математическую модель, применяемую в процессе решения экономических задач на дифференцированные платежи. Остальное дело техники и базовых математических знаний. Ну, надеюсь, что решать линейные уравнения каждый из вас умеет.
И повторюсь уже в который раз — изучайте до посинения математическую модель дифференцируемых платежей. Ссылку на эту статью я оставлял выше. Ну, ладно, так уж и быть, продублирую ее еще раз: математическая модель экономических задач на дифференцированный платеж.
Если будут трудности с пониманием того, как функционально работает схема дифференцируемых платежей, тогда записывайтесь ко мне на индивидуальную подготовку. На уроке мы с вами детально разберем все тонкости и краеугольные камни этой, уж не такой и простой, модели.
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
В данном разделе я приведу лишь условия некоторого количества задач, которые наиболее часто встречаются на официальном экзамене ЕГЭ по математике. В каждой из задач акцентировано внимание на модели дифференцируемого платежа, и только на нем.
А ведь существует масса комбинированных финансовых задач, в процессе решения которых дифференцируемый платеж занимает лишь какую-то часть решения. Все подобные задачи я разбираю со своими учениками на индивидуальных занятиях.
Пример №1
В мае планируется взять кредит в банке на сумму (10) миллионов рублей на (5) лет.
Условия его возврата таковы:
- Каждый декабрь долг возрастает на (10%) по сравнению с концом предыдущего года.
- С января по март каждого года необходимо выплатить часть долга.
- В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?
Пример №2
В июле планируется взять кредит в банке на сумму (6) миллионов рублей на некоторый срок.
Условия его возврата таковы:
- Каждый январь долг возрастает на (20%) по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил (1.8) миллиона рублей?
Пример №3
В июле планируется взять кредит в банке на сумму (20) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
- Каждый январь долг возрастает на (30%) по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась (47) миллионов рублей?
Пример №4
В июле планируется взять кредит в банке на сумму (16) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
- Каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась (38) миллионов рублей?
Пример №5
В июле планируется взять кредит в банке на сумму (6) миллионов рублей на срок (15) лет.
Условия его возврата таковы:
- Каждый январь долг возрастает на (q%) по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найти (q), если известно, что наибольший годовой платеж по кредиту составит не более (1.9) миллиона рублей, а наименьший не менее (0.5) миллиона рублей.
Пример №6
(15) января планируется взять кредит в банке на (39) месяцев.
Условия его возврата таковы:
- (1-го) числа каждого месяца долг возрастает на (q%) по сравнению с концом предыдущего месяца.
- Со (2-го) по (14-е) число месяца необходимо выплатить часть долга.
- (15-го) числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на (15-е) число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на (20%) больше суммы, взятой в кредит. Найдите (q).
Пример №7
Анатолий взял банковский кредит сроком на (9) лет. В конце каждого года общая сумма оставшегося долга увеличивается на (17%), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)?
Пример №8
Анна взяла кредит в банке на срок (12) месяцев ((1) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется (q%) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на (13%) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть (q).
Пример №9
В июле планируется взять кредит в банке на сумму (28) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
- Каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года.
- С февраля по июнь каждого года необходимо выплатить часть долга.
- В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит (9) миллионов рублей?
Пример №10
(15) января планируется взять кредит в банке на (15) месяцев.
Условия его возврата таковы:
- (1-го) числа каждого месяца долг возрастает на (1%) по сравнению с концом предыдущего месяца.
- Со (2-го) по (14-е) число каждого месяца необходимо выплатить часть долга.
- (15-го) числа каждого месяца долг должен быть на одну и ту же величину меньше долга на (15-е) число предыдущего месяца.
Известно, что восьмая выплата составила (108,000) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Не удивляйтесь, но приведенные экономические задачи на дифференцированные платежи решаются достаточно легко, если у вас присутствует детальнейшее понимание анатомии дифференцируемого платежа. Даже скажу больше, ответы на некоторые из представленных мною задач можно посчитать в уме, не прибегая к каким-либо записям и вычислениям на бумаге/компьютере.
Хотите научиться безошибочно решать подобный класс упражнений из экономического блока ЕГЭ по математике? Тогда записывайтесь ко мне на индивидуальную подготовку! Я – репетитор-практик с многолетним стажем, и главная цель моих занятий – выработать у вас навыки успешного решения экономических задач любого типа и любой сложности.
Хотите разбираться в экономических задачах на дифференцированные платежи? Тогда жду вас на уроке!
Если после прочтения данной статьи в вашей голове не все разложилось по нужным полочкам, значит, не все моменты вы уловили в процессе решения. Это не критично! Достаточно сложно стать профессиональным решателем, разбирая лишь готовые примеры. Нужно в обязательном порядке заниматься собственноручным прорешиванием.
Моя задача, как репетитора по математике, составить для вас индивидуальную программу подготовки, ориентированную на экономические задачи на дифференцированные платежи. Поэтому, если хотите стать асом в подобных задачах, то звоните мне по номеру, который опубликован в шапке данного сайта, и записывайтесь на $1$-е пробное занятие.
Я сугубо репетитор-практик, посвящающий львиную долю урока, разбору конкретных заданий. Минимум воды и максимум решений — вот мой девиз! Именно поэтому, превалирующее число моих подопечных получают высоченные баллы на официальных экзаменах ЕГЭ по математике и информатике.
И помните о том, что я достаточно востребованный репетитор, а количество учебных мест ограничено. Действуйте прямо сейчас, не откладывая принятия решения в долгий ящик.
Источник: www.videoege.ru
