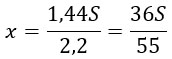Артикул: 1128368
Название или условие:
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Изображение предварительного просмотра:
Процесс покупки очень прост и состоит всего из пары действий:
1. После нажатия кнопки «Купить» вы перейдете на сайт платежной системы, где можете выбрать наиболее удобный для вас способ оплаты (банковские карты, электронные деньги, с баланса мобильного телефона, через банкоматы, терминалы, в салонах сотовой связи и множество других способов)
2. После успешной оплаты нажмите ссылку «Вернуться в магазин» и вы снова окажетесь на странице описания задачи, где вместо зеленой кнопки «Купить» будет синяя кнопка «Скачать»
ЕГЭ Математика Задание 15#513106
3. Если вы оплатили, но по каким-то причинам не смогли скачать заказ (например, случайно закрылось окно), то просто сообщите нам на почту или в чате артикул задачи, способ и время оплаты и мы отправим вам файл.
Источник: studbase.ru
Проценты и кредиты ЕГЭ 2022. Часть 2.
ЕГЭ 2022 ФИПИ. Вариант 11. Задача 15.
В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. На сколько рублей последняя выплата будет больше первой?
Первая выплата – это 10% от 1050 тысяч рублей, т.е. 105 тысяч рублей.
Итак, за 2023, 2024 и 2025 годы будут выплачены лишь проценты (по 105 тысяч рублей ежегодно), а сумма долга останется прежней, т.е. равной 1050 тысяч рублей. Обозначим эту сумму через S. Долг следует отдать двумя равными платежами. Обозначим один такой платёж через Х.
Январь. Сумма долга увеличится на 10% и составит 1,1S тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга. Тогда ему останется выплатить (1,1S-Х) тысяч рублей.
Январь. Банк начислит 10% на остаток долга.
Теперь долг равен 1,1(1,1S-Х) тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга, и долг будет погашен. Получаем равенство:
Подставляем значение S=1050 и получим:
Х=605 тысяч рублей. Это последняя выплата.
605-105=500 тысяч рублей. На столько последняя выплата будет больше первой.
Ответ: 500 000 рублей.
Экономические задачи ЕГЭ Это страница с нужной вам задачей
[МИФ] Математика ЕГЭ. Финансовая математика. Кредит на развитие бизнеса. № 513106
ЕГЭ 2022 ФИПИ. Вариант 12. Задача 15.
В июле 2022 года планируется взять кредит на пять лет в размере 220 тыс. рублей. Условия его возврата таковы: каждый январь долг возрастает на r % по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; в июле 2023, 2024 и 2025 годов долг остаётся равным 220 тыс. рублей; выплаты в 2026 и 2027 годах равны; к июлю 2027 года долг будет выплачен полностью. Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 420 тыс. рублей.
Итак, за 2023, 2024 и 2025 годы будут выплачены лишь проценты, а сумма долга останется прежней, т.е. равной 220 тысяч рублей. Обозначим эту сумму через S. Далее долг следует отдать двумя равными платежами. Обозначим один такой платёж через Х.
Январь. Сумма долга увеличится на r % и составит (1+0,01r)S тысяч рублей. Сделаем замену переменной. Пусть 1+0,01r=k. Итак, после начисления процентов сумма долга равна kS.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга. Тогда ему останется выплатить (kS-Х) тысяч рублей.
Январь. Банк начислит r % на остаток долга.
Долг станет равным k(kS-Х) тысяч рублей.
Февраль-июнь. Клиент выплатит Х тысяч рублей, которые будут полностью зачтены в счёт долга, и долг будет погашен. Получаем равенство:

Это выплачено за 2026 и 2027 годы. А за первые три года кредитования выплачивались лишь проценты: r % от взятой суммы кредита.
Эта сумма равна 0,01r ∙ 220=2,2r.
За три года (2023, 2024 и 2025 годы) будет выплачено 6,6r тысяч рублей.
Выразим r через k.
Так как 1+0,01r=k, то r=100k-100.
Следовательно, за пять лет должно быть выплачено 2X+6,6r или

Умножим обе части равенства на (1+k).
440k 2 +660k-660+660k 2 -660k=420+420k;
1100k 2 -420k-1080=0. Делим равенство на 20.
Решаем квадратное уравнение относительно переменной k>0.

Возвращаемся к переменной r.
ЕГЭ 2022 ФИПИ. Вариант 13. Задача 15.
Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1806000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено ниже.
Вариант 1. Каждый январь долг возрастает на 15% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами.
Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен.
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?
1) Рассуждаем согласно варианту 1.
Обозначим сумму кредита через S. Пусть S=1806 тыс. рублей.
1 год. Январь. Банк начислит 15%, и долг станет равным 1,15S.
Февраль-июнь. Клиент делает первый платёж, равный Х тыс. рублей. Весь этот платёж засчитывается и долг становится равным (1,15S-Х) тыс. рублей.
2 год. Январь. Банк начислит 15%, и долг станет равным 1,15(1,15S-Х) тыс. рублей.
Февраль-июнь. Клиент делает второй платёж, равный первому, т.е. Х тыс. рублей. И этот платёж полностью засчитывается. Долг погашен.
Имеет место равенство: 1,15(1,15S-Х)-Х=0. Решаем уравнение и находим значение Х.
1,15 2 ∙ S-1,15X-X = 0;
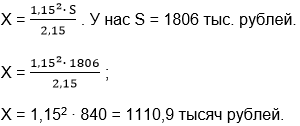
Таким образом, за два года клиент выплатит банку 2Х=2221,8 тысяч рублей или 2221800 рублей.
2) Рассмотрим условия кредитования по варианту 2.
В условии сказано: «со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца», поэтому обозначим эту величину через х тысяч рублей. Тогда вся сумма, взятая в кредит, равна 24х. Мы ее знаем, это 1806 тысяч рублей, но рассуждать удобнее с использованием введённой переменной х. Почему? Потому что проценты банк ежемесячно начисляет на остаток долга, т.е. сначала на 24х, через месяц на 23х и т.д. Подсчитаем начисленные банком проценты за всё время кредитования.
Это 2% от 24х, от 23х и т.д. Получаем:
Сумму в скобках найдём по формуле суммы первых n членов арифметической прогрессии:
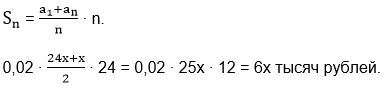
Банку нужно будет выплатить взятую сумму 24х плюс проценты 6х. Итого 30х.
Так как 24х=1806 тысяч рублей, то х=1806:24=75,25 тысяч рублей.
Итак, по варианту 2 нужно будет выплатить
30 ∙ 75,25 = 2257,5 тысяч рублей или 2257500 рублей.
Вариант 1 более выгодный, так как платить меньше, разница в выплаченных суммах составит:
Ответ: 35700 рублей.
ЕГЭ 2022 ФИПИ. Вариант 14. Задача 15.
Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1962000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено ниже.
Вариант 1. Каждый январь долг возрастает на 18% по сравнению с концом предыдущего года; с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; кредит должен быть полностью погашен за два года двумя равными платежами.
Вариант 2. 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; к 15-му числу 24-го месяца кредит должен быть полностью погашен.
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?
Задача аналогичная предыдущей. Поменялись сумма кредита и процент по 1 варианту кредитования! Ах, да! Ещё имя клиента!
1) Рассуждаем согласно варианту 1.
Обозначим сумму кредита через S. Пусть S=1962 тыс. рублей.
1 год. Январь. Банк начислит 18%, и долг станет равным 1,18S.
Февраль-июнь. Клиент делает первый платёж, равный Х тыс. рублей. Весь этот платёж засчитывается и долг становится равным (1,18S-Х) тыс. рублей.
2 год. Январь. Банк начислит 18%, и долг станет равным 1,18(1,18S-Х) тыс. рублей.
Февраль-июнь. Клиент делает второй платёж, равный первому, т.е. Х тыс. рублей. И этот платёж полностью засчитывается. Долг погашен.
Имеет место равенство: 1,18(1,18S-Х)-Х=0. Решаем уравнение и находим значение Х.
1,18 2 ∙ S-1,18X-X = 0;

Таким образом, за два года клиент выплатит банку 2Х=2506,32 тысяч рублей или 2506320 рублей.
2) Рассмотрим условия кредитования по варианту 2.
В условии сказано: «со 2-го по 14-е число каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца», поэтому обозначим эту величину через х тысяч рублей. Тогда вся сумма, взятая в кредит, равна 24х. Мы ее знаем, это 1962000 рублей. Подсчитаем начисленные банком проценты за всё время кредитования.
Это 2% от 24х, от 23х, от 22х, от 21х и т.д. до последнего месяца, когда остаток будет х тыс. рублей. Получаем:
0,02(24х+23х+22х+…+2х+х). Сумму в скобках найдём по формуле суммы первых n членов арифметической прогрессии:

Это проценты за всё время кредитования.
Банку нужно будет выплатить взятую сумму 24х плюс проценты 6х. Итого 30х.
Так как 24х=1962000 рублей, то х=1962000:24=81750 рублей.
Итак, по варианту 2 нужно будет выплатить
30 ∙ 81750 = 2452500 рублей.
Видим, что вариант 2 более выгодный, так как платить меньше, разница в выплаченных суммах составит:
Ответ: 53820 рублей.
ЕГЭ 2022 ФИПИ. Вариант 15. Задача 15.
15 января планируется взять кредит в банке на 2 года. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за 15-й месяц кредитования нужно выплатить 44 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
Решение. Обозначим через х тыс. рублей одну и ту же сумму, на которую долг будет уменьшаться ежемесячно. По сути х – это ежемесячный платёж без процентов, а в кредит на два года, т.е. на 24 месяца было взято 24х тысяч рублей. Банку нужно будет вернуть эти 24х тысяч рублей плюс проценты, которые банк будет начислять 1-го числа каждого месяца. Проценты начисляются на остаток долга.
Проценты за всё время кредитования составляют:

Итого отдать придётся 24х+3х=27х тысяч рублей.
На 15-й месяц кредитования остаток долга будет равен 10х тысяч рублей, так как на х тысяч рублей долг уменьшался ежемесячно. Проценты на этот остаток составят 0,01 ∙ 10х = 0,1. Следовательно, за 15-й месяц банком определена сумма для выплаты х+0,1х=1,1х. По условию задачи эта сумма равна 44 тыс. рублей. Решаем уравнение:
1,1х = 44 → х = 40 тыс. рублей.
Итак, за всё время кредитования банку нужно будет отдать
27 ∙ 40 = 1080 тыс. рублей = 1080000 рублей.
Ответ: 1080000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 16. Задача 15.
15 января планируется взять кредит в банке на 3 года. Условия его возвращения таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей. Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
Решение. Обозначим через х тыс. рублей ежемесячный платёж без процентов, а в кредит на три года, т.е. на 36 месяцев было взято 36х тысяч рублей. Банку нужно будет вернуть эти 36х тысяч рублей плюс проценты, которые банк будет начислять 1-го числа каждого месяца. Проценты начисляются на остаток долга.
Проценты за всё время кредитования составят:

Итого отдать банку придётся 36х+6,66х=42,66х тысяч рублей.
По условию за 24-й месяц нужно выплатить 45,2 тысяч рублей. Эта сумма складывается из ежемесячного платежа без процентов, который мы обозначили через х, и процентов на остаток вклада по прошествии 23 месяцев кредитования. Остаток будет равен 13х.
х + 0,01 ∙ 13х = 1,13х. Получаем уравнение:
1,13х = 45,2 → х = 40 тыс. рублей.
Итак, за всё время кредитования банку нужно будет отдать
42,66 ∙ 40 = 1706,4 тыс. рублей = 1706400 рублей.
Ответ: 1706400 рублей.
ЕГЭ 2022 ФИПИ. Вариант 35. Задача 15.
15 января планируется взять кредит в банке на 24 месяца. Условия его возвращения таковы: 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?
Решение. Пусть ежемесячный платеж (без процентов) составляет х рублей. Тогда кредит был выдан в размере 24х рублей. За второй год кредитования (за последние 12 месяцев) нужно вернуть 12х рублей (долг без процентов) плюс проценты, т.е. сумму процентов за каждый из последних 12-то месяцев. По условию эта сумма равна 339000 рублей. Получаем уравнение:
12х + (12х + 11х + 10х + … + х) ∙ 0,02 = 339000;
12х + (12х+х)/2 ∙ 12 ∙ 0,02 = 339000;
12х + 13х ∙ 6 ∙ 0,02 = 339000;
12х + 1,56х = 339000;
13,56х = 339000; х = 339000 : 13,56; х = 25000.
Итак, ежемесячный платеж (без процентов) составляет 25000 рублей.
За первый год кредитования (за первые 12 месяцев) необходимо выплатить:
12х + (24х + 23х + 22х + … + 13х) ∙ 0,02 = 12х + (24х+13х)/2 ∙ 12 ∙ 0,02 =
= 12х + 37х ∙ 6 ∙ 0,02 = 12х + 4,44х = 16,44х = 16,44 ∙ 25000 = 411000 рублей.
Источник: profile-mathematics.ru
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заемщика возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заемщика будет меньше 10 млн рублей.
1 год. Сумма кредита S увеличивается в 1,2 раз (на 20%) и выплачивается только процент по кредиту, т.е.
1,2S — 0,2S = S (я не буду выводить формулу, по которой мы сразу сможем найти S потому, что она получится слишком лихой; конкретно в этой задаче проще сразу подставлять нужные значения)
2 год. Аналогично с первым: увеличение суммы и выплата процентов:
3 год. Ничего не меняется, все также:
4 год. Здесь становится немного веселее, т.к. наконец-то происходит выплата части денег. И, конечно, про увеличение долга на 20% не забываем!
5 год. На оставшуюся сумму долга накладываем проценты, делаем точно такую же выплату, как и на 4-от году, и погашаем кредит:
1,44S — 1,2x — x = 0;