Что такое теория массового обслуживания?
Теория массового обслуживания относится к изучению особенностей, функций и недостатков очереди. Это математическое исследование очень актуально для исследования операций, поскольку его надлежащее применение помогает устранить узкие места в работе и сбои в обслуживании. Понятие было введено датским математиком Агнером Крарупом Эрлангом. Как правило, очередь связана с ограниченной доставкой ресурсов, и для моделирования таких процессов требуется теория массового обслуживания. Его применение позволяет менеджерам исследовать оптимальное предложение ограниченных ресурсов, необходимых для удовлетворения потребительского спроса в различных случаях.
Оглавление
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
- Что такое теория массового обслуживания?
- Как работает теория массового обслуживания?
- Пример теории массового обслуживания
- Применение теории массового обслуживания
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Теория массового обслуживания — это прежде всего анализ различных аспектов очереди или очереди ожидания.
- Его анализ помогает предприятиям более продуктивно обращаться с очередью, не нанося ущерба интересам клиентов, оптимизируя расходы и степень удовлетворенности клиентов.
- Теория включает несколько факторов. Он начинается с записи клиента или организации, затем их движения, оказанных им услуг и, наконец, выражения об услуге.
- Это помогает в разработке различных моделей очередей. Примеры его применения включают систему управления виртуальной очередью.
Как работает теория массового обслуживания?
Теория массового обслуживания в исследованиях операций способствует разработке эффективной системы массового обслуживания для бизнеса. Теория помогает профессионалам систематически изучать лучший метод и организовывать настройку. Это придает первостепенное значение балансу эффективного обслуживания и экономической жизнеспособности системы. Действующая эффективная система очередей улучшает обслуживание клиентов и повышает конкурентоспособность. Конкурентное преимущество. Конкурентное преимущество относится к преимуществу, которым пользуется компания, которая по-прежнему успешно превосходит своих конкурентов, принадлежащих к той же отрасли, путем разработки и реализации эффективных стратегий, позволяющих ей предлагать качественные товары или услуги. услуги, установление разумных цен для своих клиентов, максимальное увеличение благосостояния заинтересованных сторон и т. д., в результате чего компания может получать больше прибыли, создавать положительную репутацию бренда, увеличивать продажи, максимизировать рентабельность активов и т. д. читать далее .
Лекция 11. Системы массового обслуживания: состояния системы, характеристики клиентов и владельцев
Система очереди требует непрекращающихся импровизаций, чтобы идти в ногу с технологическим прогрессом и инновационными методами ведения бизнеса. На протяжении многих лет при проектировании системы массового обслуживания неотъемлемыми являются следующие основные факторы.
Лекция 18: Теория массового обслуживания. Системы массового обслуживания
- Прибытие: Процесс начинается с прибытия одного человека или группы людей. Они могут приходить в разные промежутки времени, и это может влиять на операции. Проверьте формирование очереди и отметьте любые отклонения в прибытии. Отслеживайте каждый аспект процесса на этом этапе.
- Движение: Эта часть в основном фокусируется на движении очереди и поведении человека. Это все равно, что следить за их действиями и смотреть, нетерпелив ли клиент или привык к ситуации. Возьмите обратную связь и посмотрите, как они на нее отреагируют. Пожалуйста, запишите, где они хотят каких-либо изменений. Много раз наблюдалось, что большие собрания в маленьком месте имеют тенденцию развивать негативные качества по отношению к бизнесу. В таком случае клиент может выбрать другой вариант. Адаптируйте необходимые меры или альтернативные процедуры, чтобы сохранить клиента и повысить эффективность.
- Сервис: это одна из жизненно важных частей процесса. Если для решения запроса потребуется больше времени, он увеличит строку. Кроме того, это может вызвать скуку и разочарование у клиентов. Лучшее понимание и применение теории важно для снижения негативного воздействия длинной очереди и длительного времени отклика.
- Выражение: Это последний шаг процесса. Важно отметить, что человек, выходящий из очереди, производит впечатление на стоящих рядом людей. Отрицательная обратная связь человека обязательно повлияет на бизнес. Поэтому следует отдавать предпочтение каждому человеку и работать с полным усердием. Идеальное выражение во многом говорит о предлагаемых ему услугах.
Давайте рассмотрим основную формулу теории массового обслуживания для системы массового обслуживания, объясняемую законом Литтла.
L= λ*W
Количество предметов в очереди = Скорость прибытия × Среднее время, проведенное в очереди
- L: среднее количество товаров или клиентов в системе,
- λ: средняя скорость прибытия,
- W: Среднее время пребывания элемента в системе.
Другая формула, основанная на модели системы массового обслуживания Эрланга, полученной из закона Литтла, выглядит следующим образом:
L = (λ – σ )/ м
- L: среднее количество товаров или клиентов в системе (длина очереди)
- λ: Скорость поступления
- σ: процент отсева
- μ: скорость отправления
Теория массового обслуживания Пример
Давайте рассмотрим пример теории массового обслуживания:
Мистер А пошел в закусочную и хотел перекусить вкусной едой. Итак, он стоит в очереди и ждет своей очереди, чтобы заказать еду. После заказа еды ему приходится ждать, чтобы получить ее, так как для ее приготовления требуется немного больше времени. Иногда длинная очередь и дальнейшее ожидание еды могут негативно повлиять на клиентов.
В этом ресторане обычно образуются очереди, и клиентам приходится ждать обслуживания. Таким образом, применяя правильную теорию очередей, ресторан может найти оптимальное решение. Основываясь на теоретическом анализе, модель работы ресторана повышает эффективность и сокращает время цикла.
Некоторые из анализов, которые могут быть получены с использованием теории в этом сценарии, включают ожидаемое время ожидания в очереди, среднее время в системе, среднее время обслуживания, среднее время ожидания у кассы, ожидаемую длину очереди, ожидаемое количество клиентов, обслуживаемых одновременно, а также вероятность того, что система будет находиться в определенных состояниях, таких как пустая или полная.
Применение теории массового обслуживания
Применение теории массового обслуживания не присуще какой-либо конкретной отрасли. Он преимущественно применяется в таких отраслях, как розничная торговля, логистика и гостиничный бизнес. Актуальность достигла пика в период пандемии Covid 19. Иметь дело с длинными очередями и решать проблемы во время возникновения пандемии COVID-19 очень беспокойно.
Предприятия внедрили различные системы управления очередями, уделяя приоритетное внимание общественной безопасности. Его использование очевидно в следующих случаях, когда вносятся изменения с учетом безопасности клиентов.
На рынке есть программное обеспечение, которое способствует виртуальному ожиданию. Система управления виртуальной очередью организует клиентов в виртуальную очередь ожидания или очередь, не ожидающую явно очереди для получения продукта или услуги. Клиенты могут ждать виртуально, используя систему управления виртуальной очередью, поскольку они не привязаны к определенной зоне ожидания.
Теория очередей помогает в процессе беспроблемной проверки в магазине. Во многих торговых точках действуют новые правила и отсутствует служба связи с клиентами. В результате розничные магазины сделали слоты, чтобы можно было отказаться от массовых сборов. Серпантинная линия с несколько касс или касс является одной из эффективных систем организации очереди, используемых в заведениях быстрого питания, так как возникновение препятствия не останавливает всю очередь; только один кассир должен решить эту запутанную проблему, в то время как остальные справляются с оставшимися трудностями.
Часто задаваемые вопросы (FAQ)
Каков пример теории очередей?
Есть много случаев, связанных с очередями, которые требуют применения теории очередей для оптимизации процесса путем устранения событий, вызывающих неэффективность. Примерами его приложений являются система управления виртуальной очередью, позволяющая использовать виртуальные очереди ожидания и извилистую очередь с несколькими кассирами.
Что такое теория массового обслуживания в исследовании операций?
Это математическое исследование имеет огромное значение для исследования операций. Предприятия могут использовать его для устранения узких мест в работе и улучшения предоставления продуктов и услуг. Кроме того, предприятия могут получить конкурентное преимущество, постоянно совершенствуя систему очередей, чтобы идти в ногу с технологическим прогрессом. Однако предприятиям следует сбалансировать эффективность обслуживания и экономическую жизнеспособность системы.
Что такое проблема теории массового обслуживания?
Это проблемы или ситуации, связанные с очередями или ожиданием и описывающие ситуацию отказа. Его исправление зависит от создания эффективной модели системы массового обслуживания на основе анализа теорий.
Рекомендуемые статьи
Это было руководство к тому, что такое теория массового обслуживания и ее определение. Здесь мы объясняем, как работает теория очередей в исследовании операций, а также приводим примеры и приложения. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:
- Статистика
- Теория принятия решений
- Нормальное распределение
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
Источник: voxt.ru
ЭММ / Лекция_Системы и модели массового обслуживания
Только сегодня: 300 рублей в подарок на первый заказ.
Какую работу нужно написать?
Другую работу
Помощник Анна
7 Системы и модели массового обслуживанияОсновные понятия Менеджеру-экономисту приходится сталкиваться с ситуациями, которые характеризуются термином системы массового обслуживания. Пример:
- обслуживание покупателей в сфере розничной торговли
- транспортное обслуживание
- медицинское обслуживание населения
- ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации
- обработка документов в системе управления
- туристическое обслуживание (билетные кассы, справочные бюро).
Системы массового обслуживания (СМО) представляют собой структуры, содержащие одно или несколько обслуживающих устройств – каналов обслуживания, на вход которых в случайные моменты времени поступают требования для обслуживания. В качестве каналов могут фигурировать технические устройства либо персонал, выполняющие функции обслуживания. Каждая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих на СМО в какие-то случайные моменты времени. Обслуживание поступившей заявки продолжается некоторое (вообще говоря, случайное) время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать. Система массового обслуживания – это система двух взаимодействующих потоков случайных событий – входного потока заявок (требований) на обслуживание и выходного потока обслуженных требований. Состояние системы – это число находящихся в СМО заявок в данный момент. Узел обслуживания – это часть СМО, через который осуществляется взаимодействие входного и выходного потока заявок. Узел обслуживания может содержать один или более обслуживающих каналов (обслуживающих устройств, приборов). Пример обслуживающего канала – рабочее место кассира на предприятии массового обслуживания. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства. Заявки, находящиеся в СМО, могут либо ожидать обслуживания, либо находиться под обслуживанием. Очередь – это часть заявок, ожидающих обслуживания. Дисциплина очереди – это правила формирования очереди. Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, а также от характера потока заявок, обладает какой-то пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективностью обслуживания. Главная особенность процессов массового обслуживания – случайность. Теория массового обслуживания опирается на теорию вероятностей и математическую статистику. Первоначально развитие теории массового обслуживания связано с именем датского ученого А.К.Эрланга (1878-1929), с его трудами в области проектирования и эксплуатации телефонных станций. Большой вклад в развитие этой теории внесли российские математики А.Я.Хинчин, Б.В.Гнеденко, А.Н.Колмогоров, Е.С. Вентцель и др. В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких систем массового обслуживания, процесс функционирования которых является марковским, то есть все потоки событий, переводящие систему из состояния в состояние, простейшие. Простейшим называется случайный поток, обладающий тремя основными свойствами: стационарности, ординарности и отсутствия последствия. Свойство стационарности обеспечивает постоянное количество требований в течение некоторого промежутка. При этом количество требований зависит только от длины этого промежутка по оси времени, т.е. это свойство не учитывает суточные и годовые колебания спроса. Свойство ординарности указывает, что вероятность поступления двух заявок одновременно является бесконечно малой величиной. Свойство отсутствия последствия состоит в том, что количество требований, поступивших в систему после времени t0 не зависит от числа требований до этого момента. Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t рóвно k требований задается формулой 
, (1) где λ – плотность потока или среднее число требований в единицу времени. Заранее условимся (чтобы не оговаривать это всякий раз отдельно), что мы будем считать все потоки событий, переводящие СМО из состояния в состояние, пуассоновскими. Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой экспоненциального закона распределения: 
, (2) где μ – интенсивность обслуживания (среднее число событий, происходящих в единицу времени), 
. (3) Классификация систем массового обслуживания иих основные характеристики Системы массового обслуживания классифицируются по разным признакам. 1) По числу каналов системы массового обслуживания могут быть одноканальными или многоканальными. 2) По месту нахождения источника требований СМО делятся на разомкнутые (когда источник требований находится вне системы) и замкнутые (когда источник находится в самой системе). 3) В зависимости от условий ожидания требованием начала обслуживания различают СМО с отказами и СМО с ожиданием. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает «отказ», покидает СМО и в дальнейшем процессе обслуживания не участвует. В СМО с ожиданием заявка, поступившая в момент, когда все каналы заняты, становится в очередь и ожидает, пока не освободится один из каналов. Как только освободится канал, принимается к обслуживанию одна из заявок, стоящих в очереди. Для систем с ожиданием важна дисциплина очереди. Различают следующие виды дисциплины очереди: а) упорядоченное обслуживание: – первый пришел – первый обслуживается (английская аббревиатура FIFO – First Input First Output); – последний пришел – первый обслуживается (английская аббревиатура LIFO – Last Input First Output); б) неупорядоченное обслуживание: заявки попадают в канал обслуживания случайным образом; в) с приоритетами: при которой некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания. 4) Системы с ожиданием делятся на системы с ограниченным ожиданием и системы с неограниченным ожиданием. В системах с ограниченным ожиданием может ограничиваться либо длина очереди либо время пребывания в очереди. В системах с неограниченным ожиданием каждая заявка, поступившая в момент, когда нет свободных каналов, становится в очередь и «терпеливо» ждет освобождения канала, который примет ее к обслуживанию. Любая заявка, поступившая в СМО, рано или поздно будет обслужена. Для анализа процесса, протекающего в СМО, важно знать основные параметры системы: 1) число каналов n, 2) число мест в очереди m, 2) интенсивность потока заявок , 3) интенсивность обслуживания (величина, обратная среднему времени обслуживания tобс: 
), 4) условия образования очереди (ограничения, если они есть). При этом все числовые данные в решаемой задаче должны быть приведены к единой единице измерения времени. В зависимости от типа СМО при оценке ее эффективности могут применяться те или характеристики эффективности работы СМО. Рассмотрим определение основных характеристик наиболее распространенных видов СМО. Многоканальная СМО с отказами. Для СМО с отказами наиболее важными характеристиками являются: 1) абсолютная пропускная способностьA – среднее число заявок, которое может обслужить система за единицу времени. 2) относительная пропускная способностьq – средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок). 3) в зависимости от задачи исследования могут быть важны и другие характеристики, например, среднее число занятых каналов 
, среднее относительное время простоя системы в целом и отдельного канала и т. д. Если требование поступает в систему в момент, когда все п каналов заняты, то оно получает отказ (покидает систему необслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца. Размеченный граф состояний системы с отказами представлен на рисунке. 
Относительная нагрузка на систему 
. Предельные вероятности состояний системы (формулы Эрланга) для рассматриваемой СМО имеют вид 
где Р0 – вероятность свободного состояния системы, Рk – финальные вероятности состояния системы (в стационарном режиме работы СМО). Вероятность отказа
Относительная пропускная способность
Абсолютная пропускная способностьA = λ q.Среднее число занятых каналов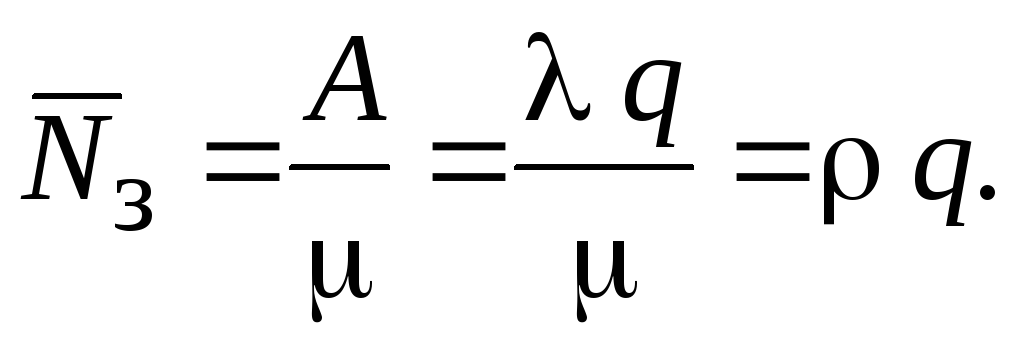
Многоканальная СМО с ожиданием. Для СМО с неограниченным ожиданием как абсолютная А, так и относительная пропускная способность q теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Зато для такой СМО весьма важными характеристиками являются: 1) среднее число заявок в очереди 
, 2) среднее число заявок в системе 
(в очереди и под обслуживанием), 3) среднее время ожидания заявки в очереди 
, 4) среднее время пребывания заявки в системе 
(в очереди и под обслуживанием), и другие характеристики ожидания. Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик: как абсолютная и относительная пропускная способности, так и характеристики ожидания. Пусть в n-канальную СМО поступает простейший поток требований с интенсивностью λ; число мест в очереди ограничено и равно т. Время обслуживания требований (для одного канала) экспоненциальное, со средним значением tобс . Размеченный граф состояний системы с ожиданием представлен на рисунке.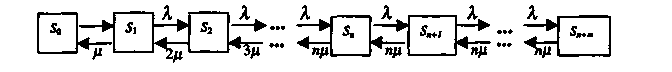 
Предельные вероятности состояний системы имеют вид 
. Требование получает отказ в том случае, когда система занята, то есть вероятность отказа 
Относительная пропускная способность или вероятность того, что поступившее в систему требование будет принято к обслуживанию, дополняет вероятность отказа до единицы: 
В систему поступает λ требований в единицу времени, а доля требований, принятых к обслуживанию, равна q. Следовательно, абсолютная пропускная способность
Каждый канал, если он занят, обслуживает в единицу времени требований, а вся система – А требований. Таким образом, среднее число занятых каналов
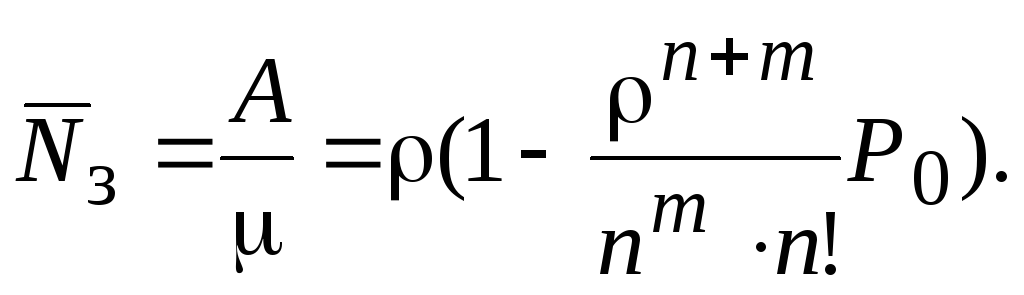Среднее число требований
, находящихся в очереди, вычислим как математическое ожидание числа требований, находящихся в очереди: 
Подставив значения Рn+r (r=1, m) и выполнив преобразования, окончательно получим 
. Учитывая, что среднее число требований, находящихся под обслуживанием, совпадает со средним числом занятых каналов, среднее число требований, находящихся в системе, равно 
. Среднее время пребывания требований в очереди
. Среднее время пребывания заявки в системе
Среднее время пребывания требования в системе получим, если к среднему времени ожидания в очереди прибавим среднее время обслуживания, умноженное на относительную пропускную способность q.Многоканальная СМО с неограниченной длиной очереди. Так как длина очереди не ограничена, то граф состояний в этом случае является бесконечным. 
Установившийся режим работы системы существует при 
, а при 
очередь будет расти неограниченно. Полагаем, что 
. Далее представлены формулы для расчета характеристик СМО с неограниченной очередью. Предельные вероятности состояний:
Так как число мест в очереди не ограничено, то все требования, поступившие в систему, рано или поздно будут обслужены. Следовательно, вероятность отказа
Среднее число занятых каналов
Среднее число требований, находящихся в очереди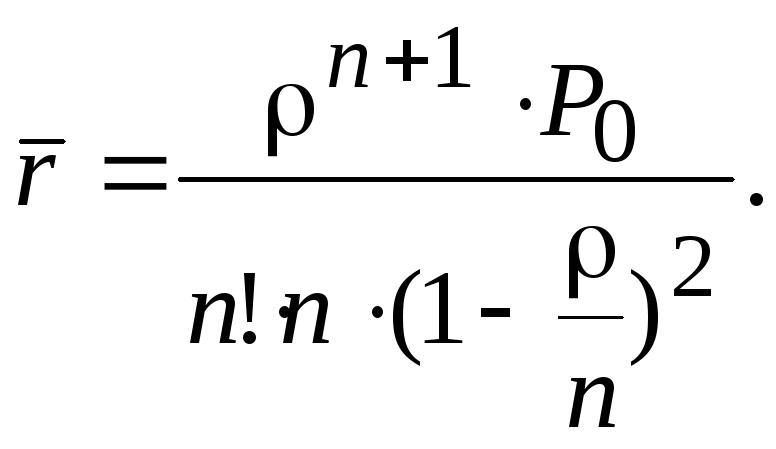
Среднее число требований, находящихся в системе
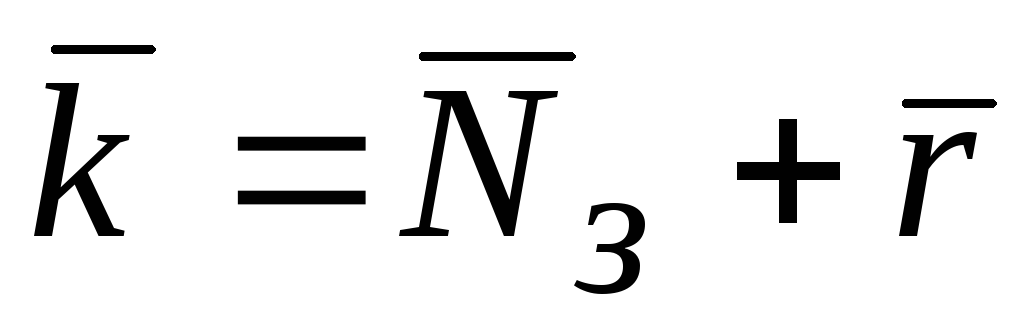Среднее время пребывания требования в очереди
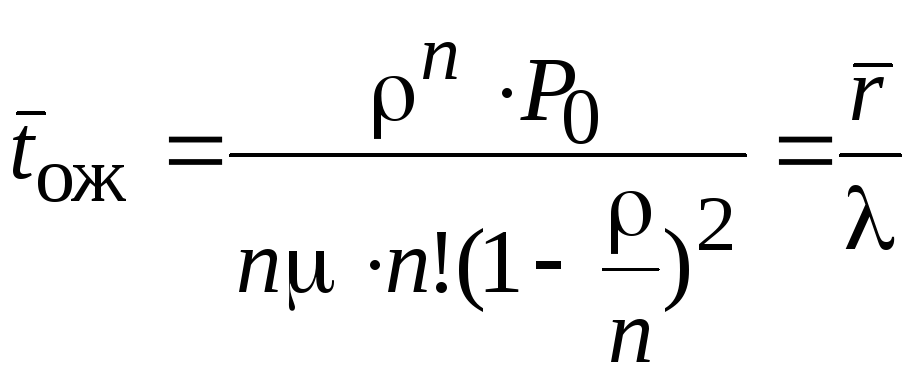Среднее время пребывания требования в системе
Ограничение
Для продолжения скачивания необходимо пройти капчу:
Источник: studfile.net
Теория массового обслуживания в экономическом анализе
Впервые теория массового обслуживания была применена в телефонии, а затем распространилась на другие отрасли хозяйственной деятельности. К примеру, нормальный процесс обслуживания покупателей связан с правильной оценкой количества организаций данного профиля торговли, необходимой численности продавцов, объемов основных фондов, периодичности завоза продукции, количества обслуживаемого населения, спроса на предлагаемые товары и т.д. Задача состоит в выборе оптимального варианта налаживания обслуживания населения, когда время на обслуживание будет минимальным, а высоким его качество и оптимальными затраты. Данные методы применяются и в производстве, например, чтобы оптимизировать работу обслуживающих подразделений. Системами массового обслуживания являются: телефонные станции, билетные кассы торговые комплексы, ремонтные мастерские, справочные бюро и т.д.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Замечание 1
Каждой системе массового обслуживания (СМО) соответствует определенное количество обслуживающих единиц, называемых каналами обслуживания. Предназначением любой СМО является обслуживание потока заявок, поступающих в разные моменты времени.
Заявка обслуживается случайное время, а после канал освобождается и готов принимать следующую заявку. Случайность появления заявок и времени их обслуживания становится причиной того, что в какой-то момент на входе СМО образуется большое число заявок, а в другой СМО работает с недогрузкой или же ее работа вообще приостанавливается по причине отсутствия заявок. Изменение состояния СМО имеет скачкообразный характер.
Предметом теории массового обслуживания является построение математической модели, которая связывает условия работы системы массового обслуживания (количество каналов, производительность и правила их работы, специфику заявок) с необходимыми характеристиками, т.е. показателями эффективности системы. Данные показатели позволяют описать способность СМО обрабатывать поток заявок. К таким показателям относятся:
«Теория массового обслуживания в экономическом анализе»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы
- Среднее количество заявок, которые обслуживаются в СМО за единицу времени;
- Среднее количество занятых каналов;
- Количество заявок в очереди;
- Время ожидания и т.д.
Теория массового обслуживания является разделом теории вероятностей. В вероятностной математической модели учитывается степень влияния случайных факторов на работы объекта (процесса, системы), а также оценивается будущее положение при вероятности наступления тех или иных событий.
Рассмотрим математическую формулировку задачи массового обслуживания. Существует некоторая система S, где осуществляется случайный процесс. Состояние данной системы изменяется с течением времени случайным образом, который заранее неизвестен. Также присутствует поток событий, т.е. последовательность событий однородного типа, которые следуют одно за другим (поток вызовов, поток отказов, поток восстановлений, поток покупателей и др.).
Системы массового обслуживания классифицируются по:
- Наличию очередей: с очередью и с отказами. В СМО с очередью поступившая заявка в момент занятости всех каналов не уходит, а оказывается в очереди и ожидает обслуживания. В СМО с отказами поступившая заявка во время занятости всех каналов получает отказ и не обслуживается в дальнейшем.
- Организации очереди: ограниченные и не ограниченные. Ограничения могут затрагивать длину очереди, время ожидания, дисциплину обслуживания.
- Зависимости потока от текущего состояния системы: открытые и замкнутые СМО. Открытая СМО не влияет на характеристику потока заявок. В замкнутой характеристики потока заявок зависят от состояния системы.
Элементы системы массового обслуживания
Каждая СМО имеет свою структуру, которая состоит из некоторого числа обслуживающих устройств, называемых каналами обслуживания. Каналами могут быть лица, которые выполняют те или иные операции (продавцы, кассиры, операторы и др.), автомашины, линии связи, и т.д.
Схема СМО представлена на рисунке 1.
Рисунок 1. Система массового обслуживания. Автор24 — интернет-биржа студенческих работ
Каждая СМО состоит из следующих основных элементов:
- Входящего потока заявок;
- Очереди;
- Каналов обслуживания;
- Выходящего потока обслуженных заявок.
Каждой СМО присуща определенная эффективность функционирования (пропускная способность), позволяющая более или менее успешно обрабатывать поток заявок.
Предмет исследования теории массового обслуживания – это системы массового обслуживания.
Цель теории заключается в выработке рекомендаций по рациональной разработке СМО, эффективной организации их функционирования и регулированию потока заявок, чтобы обеспечить высокую эффективность работы СМО.
Чтобы достичь перечисленные цели, перед теорией массового обслуживания ставятся задачи установления зависимостей эффективности работы СМО и ее организации, т.е. особенностей потока заявок, количества каналов, производительности каналов и правил работы.
Применение теории
Теория массового обслуживания является прикладной областью теории случайных процессов, в рамках которой рассматриваются вероятностные модели систем обслуживания. Данная теория применяется с целью минимизации затрат в сфере обслуживания, в торговле, в производстве.
Посредством методов математического моделирования определяется, например, оптимальное число машин, обслуживаемое одним рабочим или цехом.
Типичный пример объекта теории массового обслуживания – это автоматическая телефонная станция. На АТС поступают случайным образом вызовы абонентов (требования), обслуживание заключается в связи абонентов с другими, поддержание соединения во время разговора.
В практической деятельности теория применяется в случаях, когда массово поступают заявки на обслуживание, например, поступление материалов и сырья на склад, их выдача со склада, организация настройки, ремонта оборудования, обработка большой номенклатуры деталей, транспортные операции, расчет оптимального числа служб и отделов на предприятии и т.д.
Источник: spravochnick.ru