Не хватает прав доступа к веб-форме.
Записаться на семинар
Звездочкой * отмечены поля,
обязательные для заполнения.
Ваша заявка отправлена!
В ближайшее время с вами свяжется наш эксперт
Under construction!
Раздел находится в разработке и будет доступен в ближайшее время.
This page is under construction and coming soon.
НИСИПП
+7 495 988-92-52
- Официальная страница НИСИПП
- Проблематика МСП и его господдержка
- Банки и МСП (малый и средний бизнес)
- Антикоррупционный капитал
- О нас
- Интерактивное резюме
- Наши организации
- АНО «НИСИПП»
- ИКЦ «Бизнес-Тезаурус»
- ООО «O2Consulting»
- ООО «Л-СТАР»
- Школа
- Направления деятельности
- Наши технологии
- Мероприятия
- Новости
- Мнения наших экспертов
- Интервью
- Мониторинги
- Исследования
- Законодательство
- Наши публикации
- Программы поддержки
- Мониторинг банковского и государственного финансирования МСП

Бинарные опционы обучение | Бинарные опционы — Мои секреты технического анализа !
Главная / Исследования / Реальные опционы в управлении рисками и оценке бизнеса
Реальные опционы в управлении рисками и оценке бизнеса
Дата: 14.07.2006
Файлы
- rar rar, 29.04 КБ
(Из материалов VII международной научной конференции
«Модернизация экономики и государство», 4 — 6 апреля 2006 г.)
В докладе будут рассмотрены возможности использования индивидуальных условных срочных контрактов, так называемых реальных опционов, при анализе рисковых решений и управлении рисковыми проектами долгосрочных инвестиций. Эти контракты позволяют передавать хеджировать риск за счет его передачи другой стороне — контрагенту по данному договору.
В данном случае речь идет об обосновании условий подобных договоров, которые должны характеризовать возможности снижения риска при заключении подобных контрактов, а так же предельную стоимость подобных контрактов для стороны, хеджирующей риск. На практике применение метода реальных опционов для управления рисками предполагает поиск второй стороны, которая была бы заинтересована в заключении условного срочного контракта, выгодного стороне, хеджирующей риск.
Этот интерес определяется платой за заключение рассматриваемого срочного контракта, которую выплачивает сторона, управляющая риском, своему контрагенту. В докладе будут проанализированы относительно простые методы определения предельного значения подобной платы на основе прироста ожидаемой чистой настоящей стоимости и оценки стоимости эквивалентного портфеля. Эти методы могут быть использованы так же для определения стоимости рисковых инвестиций, или в более широком смысле — стоимости рискового капитала или бизнеса в целом, под которым будем понимать текущую стоимость будущих доходов от этого бизнеса. Под эквивалентным портфелем, состоящим из рисковых и безрисковых активов, понимается портфель, обеспечивающий в будущем такие же доходы, что и рассматриваемые проекты или бизнес. В настоящее время методы оценки инвестиций на основе эквивалентных портфелей – в более широком смысле стоимости рискового капитала или стоимости бизнеса – рассматриваются как одно из важнейших современных направлений развития теории инвестиций, обоснования инвестиционных проектов, оценки стоимости рискового капитала.
Лекция 21. Сущность реальных опционов
Одновременно, одними из основных методов анализа и управления рисками в настоящее время становятся методы, основанные на использовании реальных опционов при анализе рисковых решений и управлении рисковыми проектами долгосрочных инвестиций и определении стоимости рискового капитала. Во-первых, под реальными опционами понимают индивидуальные условные срочные контракты, которые позволяют хеджировать риск за счет его передачи другой стороне — контрагенту по данному договору. Второй формой реальных опционов, выступают так называемые внутренние реальные опционы, которые представляют собой намерение собственников или менеджеров, осуществить те или иные действия по развитию бизнеса.
При управлении рисками реальных инвестиций и оценке стоимости реального рискового капитала речь идет о ситуации, когда рассматривается некоторый совершенно новый объект, которого либо вообще не было на рынке, либо его обращение на рынке носит индивидуальный характер. Речь идет о субъективных оценках риска. На первый план выступает не столько определение той или иной общей или обобщающей меры риска, сколько управление рисками, которое должно быть направлено как на защиту от неблагоприятного воздействия рыночных условий, так и на использование благоприятной рыночной конъюнктуры для развития бизнеса и создания конкурентных преимуществ.
Реальные опционы можно рассматривать как определенный аналог рыночного опциона. Но существенное отличие состоит в том, что рыночный опцион представляет собой инструмент рынка срочных контрактов, который имеет текущую рыночную цену, и операции с которым приносят определенный доход его владельцам. Реальный опцион может представлять собой индивидуальный, не рыночный, условный срочный контракт, который используется для управления рисками, и представляет интерес только для участников этого контракта или опционного соглашения. Его можно рассматривать как аналог рыночного опциона — с той разницей, что он не является ценной бумагой. Передача рисков бизнеса, обеспечивающая защиту от неблагоприятного развития рыночной конъюнктуры, или, наоборот, прием дополнительного риска на себя, позволяющий использовать преимущества благоприятного развития этой конъюнктуры, с помощью реальных опционов, основаны на заключении условного срочного контракта, предполагающего формирование определенных прав вытекающих из этого контракта, позволяющих изменить распределение будущих рисковых доходов.
Применение реальных опционов обоих типов позволяет, управлять рисками, обеспечивая подстраивание бизнеса под изменяющиеся условия внешней среды, и одновременно оказывает существенное влияние на стоимость капитала и общую оценку бизнеса. При использовании реальных опционов для управления рисками наиболее существенными являются три основные проблемы: Во-первых, необходимо определить цену, которую целесообразно платить за заключение соответствующего срочного контракта (цену реального опциона). Во-вторых, следует установить, насколько заключение соответствующего контракта позволяет изменить риск. В-третьих, речь идет о том, в какой степени заключение реального опциона меняет распределение значений конкретных показателей будущих результатов.
При определении стоимости реального опциона в докладе будут рассмотрены два указанных выше метода: на основе ожидаемого значения чистой настоящей стоимости и стоимости эквивалентного портфеля.
Источник: nisse.ru
3.3. Метод реальных опционов
Метод реальных опционов (теория выбора) — техника финансового анализа.
Оценка инвестиционных проектов методом реальных опционов основана на предположении, что любая инвестиционная возможность для компании может быть рассмотрена как финансовый опцион, то есть компания имеет право, а не обязательство создать или приобрести активы в течение некоторого времени.
Существуют два типа опционов:
- «колл» — право купить по фиксированной цене;
- «пут» — право продать по фиксированной цене.
Преимущества метода реальных опционов
1) Гибкость в принятии решений.2) Обоснованность стратегических решений3) Комплексность в оценке инвестиционных проектовНедостатки: Экономическая выгода финансового опциона полностью принадлежит его владельцу. Ни один из участников рынка не может присвоить себе даже малую часть этой выгоды.
Совсем иная ситуация складывается с реальными опционами. В большинстве случаев размер экономической выгоды может быть изменен другими участниками рынка. На развитом рынке экономическая выгода может быть только временной, и достаточно сложно предсказать, когда другие участники рынка смогут ответить на изменившуюся ситуацию.
При олигополии любой прорыв со стороны одной организации неизбежно повлечет ответные акции конкурентов, что также изменит размер экономической выгоды. В случае монополии реализация проекта может привести к увеличению привлекательности и прибыльности рынка, что в свою очередь приведет к попыткам вторжения на рынок других компаний.
В этом случае описание проекта при помощи теории оценки деривативов будет являться неполным и вряд ли сможет обеспечить исследователя необходимой информацией для принятия решения. Виды реальных опционовОпцион на выбор времени принятия решения об осуществлении капитальных инвестиций.
Опцион роста — дополнительные возможности, которые могут появиться после того как сделаны первоначальные инвестиции. Опцион изменения масштаба — увеличение или сокращение масштабов производства в течение жизненного цикла проекта. Опцион на отказ от реализации проекта — отказ от наиболее нерентабельных проектов. В таблице приведены примеры возможных реальных опционов в отношении разных типов активов. Таблица 3.3 Реальные опционы в зависимости от вида актива
| АКТИВ | ВОЗМОЖНЫЕ РЕАЛЬНЫЕ ОПЦИОНЫ |
| Инвестиционные возможности | Возможность отложить инвестиции. Уменьшение масштаба операций и экономия части начальных инвестиций (например, внедрение нового продукта) |
| Производство | Расширение производства при вложении дополнительных инвестиций. Работа с разными ресурсами или выпуск различных продуктов |
| Машины / оборудование | Перевод на режим простоя (когда доходы меньше переменных затрат) Продажа по остаточной стоимости |
| Контракт | Условия прекращения (возобновления) контракта |
| Технологический патент | Продажа, передача лицензии или сохранение прав за собой |
Методы оценки стоимости реальных опционов Для оценки стоимости реальных опционов используются два основных метода:
- модель оценки стоимости опционов Блэка—Шоулза;
- биномиальная модель.
Модель оценки стоимости опционов Блэка-Шоулза Данная модель проста как в изложении, так и в применении. Однако она имеет ряд ограничений:
- оцениваемый актив должен быть ликвидным (необходимо наличие рынка для оцениваемого актива);
- изменчивость цены актива остается одинаковой (то есть не происходит резких скачков цен);
- опцион не может быть реализован до срока его исполнения (европейский опцион).
Расчет стоимости реального опциона осуществляется по формуле Блэка-Шоулза, разработанной для оценки финансовых опционов типа «колл»: С = N(d1) х S — N(d2) х PV(X), где С — стоимость реального опциона; N(d) — интегральная функция нормального распределения; 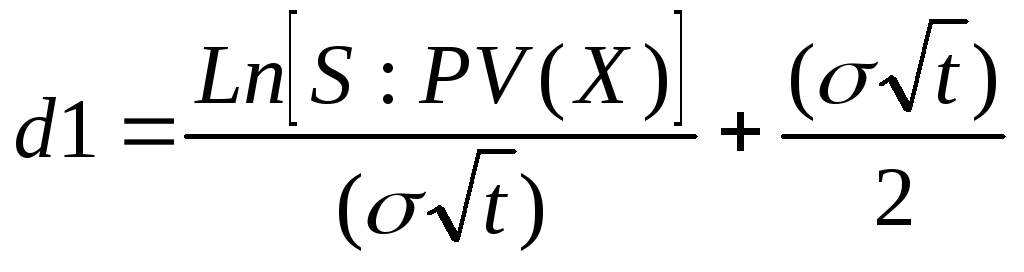
 , где σ — стандартное отклонение доходности акций за период. Для реальных опционов это «изменчивость цены активов» (рыночно оцененный риск). Для реальных активов обычным способом оценки является анализ статистических данных за прошлые периоды; S — текущая стоимость акций. Для реального опциона это приведенная стоимость денежных потоков от реализации той инвестиционной возможности, которую компания получит в результате осуществления инвестиционного проекта; PV(X) = Xe -rt — приведенная стоимость инвестиций на осуществление проекта или ликвидационной стоимости при отказе от проекта; Х — цена исполнения опциона (для реальных опционов это затраты на осуществление проекта); e — число, являющееся основанием натурального логарифма (округленное значение 2,71828); r — краткосрочная безрисковая ставка доходности; t — время до истечения срока исполнения опциона (реализации содержащейся в опционе возможности) или время до следующей точки принятия решения. Из анализа этой формулы следует, что цена реального опциона тем выше, чем:
, где σ — стандартное отклонение доходности акций за период. Для реальных опционов это «изменчивость цены активов» (рыночно оцененный риск). Для реальных активов обычным способом оценки является анализ статистических данных за прошлые периоды; S — текущая стоимость акций. Для реального опциона это приведенная стоимость денежных потоков от реализации той инвестиционной возможности, которую компания получит в результате осуществления инвестиционного проекта; PV(X) = Xe -rt — приведенная стоимость инвестиций на осуществление проекта или ликвидационной стоимости при отказе от проекта; Х — цена исполнения опциона (для реальных опционов это затраты на осуществление проекта); e — число, являющееся основанием натурального логарифма (округленное значение 2,71828); r — краткосрочная безрисковая ставка доходности; t — время до истечения срока исполнения опциона (реализации содержащейся в опционе возможности) или время до следующей точки принятия решения. Из анализа этой формулы следует, что цена реального опциона тем выше, чем:
- выше приведенная стоимость денежных потоков (S);
- ниже затраты на осуществление проекта (Х);
- больше времени до истечения срока реализации опциона (t);
- больше риск (s).
При этом наибольшее влияние на увеличение стоимости опциона оказывает приведенная стоимость ожидаемых денежных потоков. Следовательно, для повышения инвестиционной привлекательности проекта компаниям целесообразнее сосредоточиться на увеличении доходов, а не на снижении расходов.
Основные трудности, которые могут возникнуть при применении этой модели, связаны с получением достоверных исходных данных, необходимых для расчета (время до реализации заложенных в проекте возможностей, значение дисперсии и т. д.) Использование модели Блэка-Шоулза осложнено тем, что в расчетах всегда будет присутствовать множество параметров, которые носят оценочный характер, к примеру, значение приведенной стоимости денежных потоков от реализации оцениваемой возможности, значение дисперсии и т. д. Не стоит надеяться получить значимые результаты от применения даже самой новейшей формулы. Необходимо глубокое понимание метода и данных, используемых для расчета.
При оценке инвестиционного проекта методом реальных опционов вопрос определения размера дисперсии был решен путем формирования нескольких вариантов денежных потоков в зависимости от ряда факторов. На основании полученных данных о колебании объема поступления денежных средств был рассчитан показатель дисперсии, который использовался в модели Блэка-Шоулза. Таким образом, формула Блэка-Шоулза подходит для оценки простых реальных опционов, имеющих единственный источник неопределенности и единственную дату решения. Биномиальная модель Техника построения биномиальной модели является более громоздкой, чем метод Блэка-Шоулза, но позволяет получить более точные результаты, когда существует несколько источников неопределенности или большое количество дат принятия решения. В основе модели лежат два допущения:
- в одном интервале времени могут быть только два варианта развития событий (худший и лучший);
- инвесторы нейтрально относятся к риску.
Простейший пример использования биномиальной модели для расчета стоимости инвестиционного проекта уже был использован в нашей статье в примере. Напомним, что мы рассматривали проект с одним интервалом времени и двумя вариантами реализации решений. Для каждого варианта была оценена вероятность наступления и рассчитана стоимость реального опциона.
Вычисление стоимости опциона данным методом, по сути, представляет собой движение по «дереву решений», где в каждой точке менеджеры стараются принять наилучшие решения. В итоге денежные потоки, возникающие как следствие будущих решений, сводятся к приведенной стоимости.
Однако в реальной жизни «дерево решений», как правило, имеет гораздо больше узлов принятия решений. t=0 t=1 t=2 t=3 Условные обозначения: t – период, s – первоначальная стоимость актива, u – рост стоимости, d – снижение стоимости. 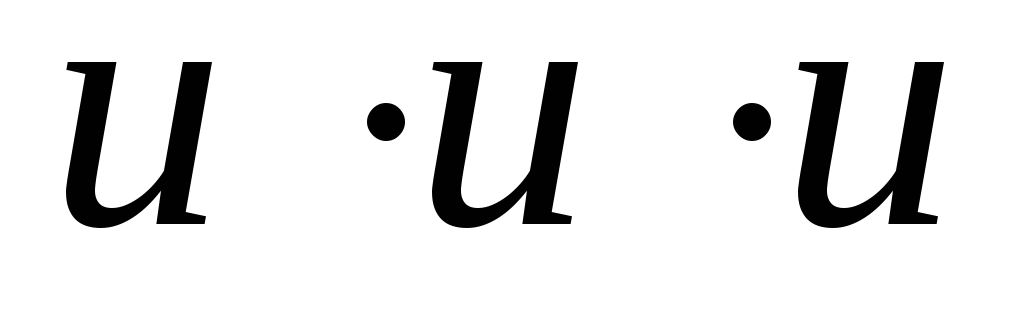





 u
u 

 u
u 



 s
s 
 d
d 
 d
d 
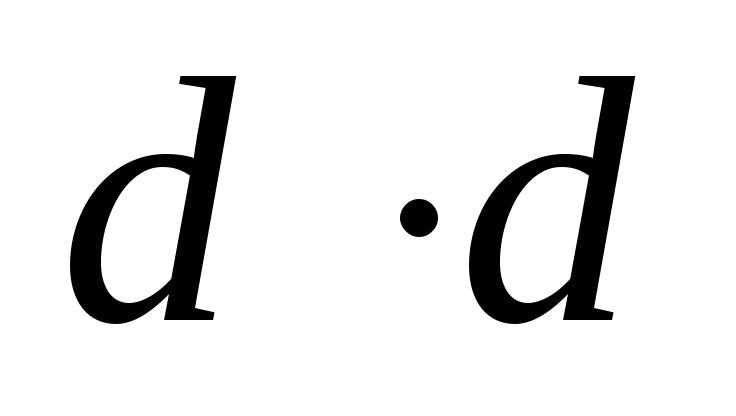
 Рис.
Рис.
2.3. «Дерево решений» трехступенчатой биноминальной модели При построении «дерева решений» с большим количеством дат принятия решений применяются те же принципы расчета стоимости реального опциона, что и для рассмотренной выше одноступенчатой модели. Однако чем больше узлов принятия решений, тем сложнее сделать оценку.
На практике основные трудности использования биномиальной модели связаны с определением значений относительного роста и снижения стоимости бизнеса в каждом периоде, а также вероятностей положительного и негативного варианта развития событий. Для расчета этих параметров разработаны соответствующие формулы.
Возможный рост стоимости бизнеса рассчитывается как: u = es, где u — относительный рост (значение данного параметра, например 1,25, означает ожидаемый рост стоимости проекта в 25%); s — стандартное отклонение среднегодовой стоимости проекта; h — интервал как часть года (к примеру, h = 0,5, если решение по проекту принимается раз в полгода). Относительное снижение стоимости (d) рассчитывается по формуле d = 1 / u. Тогда вероятность относительного роста (П), исходя из предположений о нейтральном отношении к риску, можно рассчитать как: П = [(1 + r) — d ] / (u – d).
Соответственно вероятность снижения стоимости проекта будет равна 1- П. Оценка стоимости реальных опционов с помощью биномиального метода при достаточно большом количестве дат принятия решений на протяжении года будет близка к значению, полученному с использованием модели Блэка-Шоулза. Модель Блэка-Шоулза и биномиальная модель математически эквивалентны. Но поскольку при традиционном экономическом анализе используется такая модель, как «дерево принятия решений», то биномиальная модель представляется нагляднее и проще для применения. Основной ее недостаток — громоздкость расчетов и вычислений, но вместе с тем она позволяет учесть все дополнительные факторы и сценарии развития проекта.
Источник: studfile.net
Методы опционов оценке бизнеса
В статье рассматривается проблематика разработки и совершенствования метода оценки реального опциона, основанного на известной модели Блэка-Шоулза. Модель Блэка–Шоулза в приложении к реальным опционам дает возможность определить прогнозную опционную стоимость проекта с определенной долей риска, при этом учитывается возможность гибкой реакции компании на изменения факторов внешней и внутренней сред, влияющих на основные параметры проекта. В качестве новации предложено в расчетах стоимости базового актива, закладываемой в стоимость опциона, учитывать уровень его специфичности, рассчитываемой по предложенной авторами методике. Учет специфичности базового актива, как показали модельные расчеты, позволяет повысить точность оценок стоимости опциона и обоснованность инвестиционного решения, выбираемого с его учетом.

финансовый опцион
реальный опцион
модель блэка-шоулза
инвестиционный анализ
инвестиционный проект
оптимизация
поэтапное инвестирование
1. Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов. Теория и Практика. 5-е издание. – М.: Изд-во Поли Принт Сервис, 2015. – 1300 с.
2. Лившиц В.Н. Тридцать три типовых заблуждения при оценке эффективности реализуемых в России инвестиционных (инновационных) проектов. В книге: мобильный бизнес: перспективы развития и реализации систем радиосвязи в России и за рубежом сборник материалов (тезисов) XXXVII международной конференции РАЕН. 2016. С. 13-14.
3. Fischer Black and Myron S. Scholes. «The Pricing of Options and Corporate Liabilities,» Journal of Political Economy, 81 (3), 637–654 (1973).
4. S III международной научной конференции – Соколовские чтения «Бухгалтерский учет: взгляд из прошлого в будущее; международной весенней конференции молодых ученых-экономистов «Наука молодая». 2015. – С. 384.
10. Hull, John Options, futures, and other derivatives / John C. Hull, University of Toronto. – 2015. – Ninth edition.
11. Пономарева И.А., Богаткина Ю.Г., Еремин Н.А. Экономико-математическая оценка нефтегазового месторождения методом реальных опционов с применением факторов риска. Нефтяное хозяйство. Изд-во: Нефтяное хозяйство, 2015. С. 12-14.
12. Формула Блэка-Шоулза для определения стоимости опциона и принятия инвестиционных решений [Электронный ресурс]. URL: https://financc.ru/investicii/formula-bleka-shoulza.html (дата обращения: 29.09.2019).
13. Международное рейтинговое агентство [Электронный ресурс]. URL: https://www.standardandpoors.com/ (дата обращения: 16.10.2019).
В конце XX – начале XXI вв. в связи с усложнением организационной структуры компаний и на фоне масштабной трансформации технологий и экономической конъюнктуры рынков теория и практика инвестиционного анализа и проектирования столкнулись с проблемой достоверной оценки новых инструментов принятия решений. Ключевое значение получила парадигма стоимости активов, которая предполагает оценку эффективности бизнеса не по абсолютным показателям валовой или чистой прибыли.
Возникшее понятие стоимости предполагает качественно новые подходы к оценке качества управления бизнесом в условиях быстрой смены технологических укладов, высокой изменчивости рынков готовой продукции и факторов производства, появления новых рисков, роста трансационных издержек на фоне укрупнения бизнеса. Изменившиеся экономические условия управления бизнесом предопределили появление качественно новых подходов к анализу и управлению проектами, особенно в венчурном бизнесе, где инвестиции оказывают непосредственное влияние на стоимость компании [1].
Традиционные и хорошо зарекомендовавшие себя подходы, математические модели и методы анализа инвестиционных проектов с использованием методологии чистой приведенной стоимости, основанной на анализе дисконтированных денежных потоков, принимаются экономическим сообществом с большой долей осторожности, т.к. они не позволяют должным образом учесть возможную гибкость менеджмента при адаптации управленческих решений в ответ на неожиданные изменения на рынке. Действительно, метод чистой приведенной стоимости предполагает наличие некоторого сценария изменения денежных потоков и пассивную приверженность менеджмента к изначально выбранной стратегии [2]. Однако реальные рынки характеризуются неопределенностью и значительными изменениями конъюнктуры даже в краткосрочной перспективе. По мере поступления новой информации и уменьшения неопределенности касательно рыночной ситуации менеджмент должен использовать гибкие инструменты оперативного реагирования и изменения первоначальной стратегии с целью извлечь выгоду из благоприятных будущих возможностей или уменьшить текущие потери.
Такая гибкость свойственна финансовым опционам, а в области инвестиционной оценки – стратегическим или реальным опционам. В связи с этим традиционные модели инвестиционного анализа могут быть дополнены, а в некоторых случаях заменены альтернативными подходами, например, методом оценки текущей стоимости опциона колл (пут) с использованием формулы Блэка-Шоулза-Мертона [2]. Эти подходы позволяют нивелировать указанные выше недостатки традиционных методов, но предполагают корректное использование включенных в них параметров и переменных, а главное, – предположений, на основе которых эти формулы выведены.
Напомним, что модель Блэка-Шоулза или Блэка-Шоулза-Мертона представляет собой математическую модель динамики финансового рынка, содержащего производные инвестиционные инструменты [3]. Это модель ценообразования опционов, используемая для предсказания тенденции изменения рыночной цены или дохода во времени, а также изменения стоимости финансовых инструментов, таких, например, как акции.
Рассмотрим вывод классической формулы – модели ценообразования опционов Ф. Блэка – М. Шоулза. Сделаем некоторые предположения.
Важнейшее заключается в том, что цена премии опциона испытывает дискретное логарифмическое блуждание:
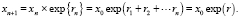
(1)
Если итоговая доходность через n торговых дней является случайным числом с распределением Гаусса r = μ + σε, то распределение цены опциона характеризуется логнормальным распределением:
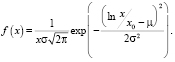
(2)
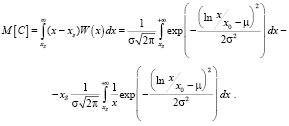
(3)
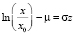
В первом интеграле (3) сделаем замену , получаем
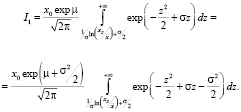
(4)
Заметим, что среднее значение (медиана) 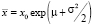 . Нижний придел объясняется эквивалентным равенством
. Нижний придел объясняется эквивалентным равенством 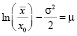 . Следовательно, выделяя полный квадрат последнем интеграле и заменяя z – σ = t, а также учитывая симметрию нормального распределения, наблюдаем, что этот интеграл преобразуется к виду:
. Следовательно, выделяя полный квадрат последнем интеграле и заменяя z – σ = t, а также учитывая симметрию нормального распределения, наблюдаем, что этот интеграл преобразуется к виду:
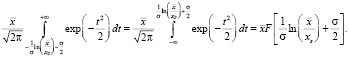
(5)
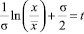
Во втором интеграле (3) делаем замену . Получаем на основе тех же суждений равенство:
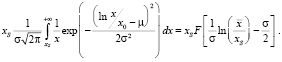
(6)
Объединяя оба интеграла, получим выражение:
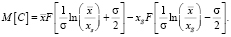
(7)
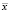
Здесь M[C] средняя цена call – опциона, – средняя цена, F[y] – интегральная функция распределения нормального закона с единичной дисперсией и нулевым математическим ожиданием.
Если учитывать изменения стоимости во времени, то необходимо сделать провести уточнение выражения (7). Пусть актив на интервале Т оценен как 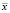 , а процентная ставка составляет величину υ, тогда сегодняшняя его стоимость
, а процентная ставка составляет величину υ, тогда сегодняшняя его стоимость 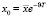 . Аналогично с ценой опциона:
. Аналогично с ценой опциона: 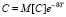 . В результате получим известную формула Ф. Блэка и М. Шоулса:
. В результате получим известную формула Ф. Блэка и М. Шоулса:
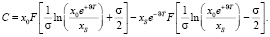
(8)
ЗФормула (8) ценообразования опционаи её аналоги произвели большой социальный резонанс, вызвали споры и восторженные отклики. Действительно, благодаря свойством нормального и логнормального распределений формула и выводится, и выглядит изящно. С течением времени представления о практической пользе этой формулы, например, для формирования оптимального портфеля, подверглись критике, стало очевидно, что, являясь вкладом в математическое моделирование процессов, протекающих на финансовых рынках, формула (8) не в полной мере адекватна рыночной практике: финансовые рынки- нестационарны, волатильность изменяется со временем, простое логарифмическое блуждание оказывается достаточно грубым приближением к реальности, непрерывная реструктуризация портфеля затруднена.
Тем не менее, модель (8) широко используется (часто с корректировками и исправлениями) участниками рынка опционов, при управлении рисками в страховании, торговле на фондовом рынке и инвестировании, находит широкое применение в практике анализа инвестиционных проектов при оценке капитальных вложений в разных отраслях: горнодобывающей, перерабатывающей, машиностроении и др.
Институциональные инвесторы широко используют модель (8) при составлении портфеля ценных бумаг, соответствующего их инвестиционным целям. Производные финансовые инструменты часто являются дешевым и эффективным способом изменения инвестиционного микса портфеля. Производные инструменты можно использовать для изменения воздействия портфеля на определенный риск. Например, в случае, когда портфельный менеджер входит в длинную позицию в фьючерсном контракте, это определяет такой же тип риска, как и владение базовой ценной бумагой: дешевле и эффективнее использовать фьючерсный контракт, чем покупать базовую ценную бумагу. Производные инструменты могут также обеспечивать защиту от падения путем покупки опционов на покупку или заключения короткой позиции в фьючерсном контракте.
Многие продукты, которые продаются розничным инвесторам в настоящее время, содержат встроенные опционы, и потребитель покупает пакет в виде полного контракта. Например, договоры страхования жизни и сбережений содержат встроенные производные инструменты. В США примером являются так называемые аннуитеты с индексом акций (определенная денежная сумма, которую ежегодно выплачивают кредитору в счет погашения полученного займа, включая проценты, зависящие от выбранного фондового индекса).
Эти продукты включают опционную функцию, которая позволяет клиенту извлекать выгоду из хорошей работы на фондовом рынке. Как правило, такие контракты будут содержать встроенный опцион колл в портфеле акций, например, на индекс S
— принятие решений об инвестициях. В этой ситуации опционом является эффект от реализации проекта в условиях изменения конъюнктуры рынка. Чаще всего речь идет о таких крупных проектах, как переключение с одного источника энергии на другой (в случае, если значительно изменяются цены на газ или электричество), закрытие и повторное открытие производства (например, при падении цен на металлы и комплектующие) и др.;
— определение стоимости новых финансовых инструментов или оценка специфических активов по заказу клиента. Модель Блэка-Шоулза активно используется инвестиционными банками при решении этой задачи;
— реальные опционы. Речь идет о том, что собственный капитал компании может быть представлен в виде опциона-колл с учетом того, что собственник бизнеса в любой момент может его ликвидировать [5].
Логика реальных опционов основана тех же принципах, что и теория финансовых: реальный опцион, как и финансовый, создает значительную гибкость в оценке альтернатив для инвестирования. Анализ на основе реальных опционов позволяет определить, когда и в каком объеме необходимо выполнять конкретные капитальные вложения. Таким образом, процесс принятия решений, основанный на реальных опционах, является приближением к инвестированию и оценке в условиях высокой неопределенности и риска [6].
Ярким примером возможностей использования метода реального опциона является случай корпорации, рассматривающей покупку или продажу участков земли, содержащих месторождения золота. Если чистая приведенная стоимость (net present value, NPV) проектов по добыче золота оказывается положительной, компания начинает разработку соответствующих участков [7]. Если же участки оцениваются как неперспективные (таких может быть большинство, поскольку необходимые издержки, как правило, оказываются слишком высокими по сравнению с ожидаемыми доходами), их разработка откладывается. Чтобы избавиться от малопривлекательных для инвестиций участков, требующих расходов, корпорация принимает решение выставить их на продажу. Ее руководители полагают, что другие фирмы могут заинтересоваться предложением дешево приобрести права на разработку участков, подходящих им с географической или стратегической точки зрения [5].
Менеджерами компании, выполняющим программу реализации активов, предложено изменить способ расчета стоимости участков. Обычный подход заключается в том, чтобы определить стоимость участка, если начать освоение немедленно. Суть нового метода состоит в оценке самой возможности начать эксплуатацию участка в будущем, если объем извлекаемых запасов золота возрастет в результате внедрения новых технологий добычи. Иными словами, руководство корпорации должно применить к условиям своей отрасли идею, заложенную в опционах.
С помощью простой финансовой модели менеджеры могут определить опционную стоимость участков на пять лет вперед, учитывая неопределенность в отношении запасов золота и будущих цен на него, а также возможность гибкой реакции компании на изменения этих факторов. После переоценки портфеля руководители могут принять решение сохранить те участки, опционная стоимость которых окажется высокой, а остальные выставить на продажу уже не по символической цене, а по соответствующей их истинной стоимости [5].
Общий вид модели Блэка-Шоулза расчета стоимости финансового опциона, используемый далее, следующий:
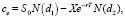
(9)
где ce – премия европейского опциона колл; S0 – курс спот акции; X – цена исполнения опциона; N(d) – функция нормального распределения; N(d1) – риск-нейтральная вероятность события, что опцион принесёт выигрыш; N(d2) – как вероятность события, что опцион будет исполнен. Модель Блэка-Шоулза-Мертона однозначно отражает влияние ключевых параметров на стоимость опциона (таблица 1).
Влияние параметров модели Блэка-Шоулза на стоимость опциона (колл)
Влияние на цену опциона
Текущая цена базового актива S0
Источник: vaael.ru
