Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Прежде чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода.
Первый период (конец 60-х–начало 70 годов) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, основанных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике.
Теория нечетких моделей и приложения семантических технологий
Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.
Математический аппарат
Проиллюстрируем это на простом примере. Формализуем неточное определение «Горячий чай». В качестве xx (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяться от 0 до 100 градусов. Нечеткое множество для понятия «Горячий чай» может выглядеть следующим образом:
Так, чай с температурой 60С принадлежит к множеству «Горячий» со степенью принадлежности 0.80. Для одного человека чай при температуре 60С может оказаться горячим, для другого — не слишком горячим. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое «И»):
Объединение двух нечетких множеств (нечеткое «ИЛИ»):
Что такое модель компетенций и в чем её польза для бизнеса?
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения — наиболее распространенные случаи t-нормы и t-конормы.
Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.
Нечеткая переменная описывается набором (N,X,A), где N — это название переменной, X — универсальное множество (область рассуждений), A — нечеткое множество на X.
Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:
- названия;
- множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;
- универсального множества X;
- синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;
- семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.
Рассмотрим такое нечеткое понятие как «Цена акции». Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: «Низкая», «Умеренная», «Высокая» и зададим область рассуждений в виде X=[100;200] (единиц). Последнее, что осталось сделать — построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.
Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности.
Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке xx вычисляется согласно выражению:
При (b−a)=(c−b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).
Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):
При (b−a)=(d−c) трапецеидальная функция принадлежности принимает симметричный вид.
Функция принадлежности гауссова типа описывается формулой:
и оперирует двумя параметрами. Параметр cc обозначает центр нечеткого множества, а параметр σ отвечает за крутизну функции.
Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике. На рисунке 3 приведен пример описанной выше лингвистической переменной «Цена акции», на рисунке 4 – формализация неточного понятия «Возраст человека». Так, для человека 48 лет степень принадлежности к множеству «Молодой» равна 0, «Средний» – 0.47, «Выше среднего» — 0.20.
Источник: vc.ru
Нечеткие модели в бизнесе
Предложена формальная постановка обобщенной задачи выбора бизнес-системы в нечетких условиях. Разработана модель выбора в виде нечеткого реляционного уравнения.
Произведена структурная идентификация модели в классе композиций нечетких соответствий на базовых множествах, состоящих из списка возможных бизнес–систем, списка предполагаемых объектов для строительства и укрупненных критериев оценки надежности бизнес-систем. Получено явное выражение для функции принадлежности искомого решения в общем виде, представляющего собой нечеткое соответствие на декартовом произведении множеств объектов и предлагаемых бизнес-систем. Предложены формулы получения частных решений задачи при использовании наиболее известных треугольных норм в виде логического, алгебраического и граничного произведения, и индуцированных этими нормами импликаторов. Так как обратная задача выбора модели бизнес-системы является трудной и не всегда разрешимой, то предложена методология решения обратной задачи, путем ее сведения к проблеме оптимизации что позволяет найти искомое нечеткое соответствие, которое в наивысшей степени отвечает условию минимизации критерия оптимизации – нормы отклонения расчетных величин от наблюдаемых. Выполнена практическая апробация разработанной методологии решения проблемы в виде контрольного решения прямой и обратной задач для всего спектра исследуемых норм и импликаторов в среде пакета компьютерной математики.

бизнес-система
нечеткое моделирование
нечеткие соответствия
1. Айзинов С.Д., Сазонов А.Е., Солодовниченко М.Б. Разработка нечеткой модели выбора вида профессиональной деятельности выпускниками вуза // Вестник Государственного университета морского и речного флота имени адмирала С О. Макарова. 2017. № 6 (46). С. 1330–1337.
2. Новиков А.В. Методология нечеткого принятия решений и алгоритмизация управления оказанием медицинской помощи больным пиелонефритом: дис. . докт. мед. наук: 14.00.40. Курск, 2009. 232 с.
3. Пантина Т.А., Сазонов А.Е. Нечеткая модель для выбора бизнес системы // Транспортное дело России. 2018. № 6 (139). С. 239–241.
4. Блюмин С.Л., Шуйкова И.А., Сараев П.В., Черпаков И.В. Нечеткая логика: алгебраические основы и приложения. Липецк: ЛЭГИ, 2002. 111 с.
5. Осипов Г.С. Исследование соответствий в задаче нечеткой диагностики // Вопросы современной науки: коллект. науч. монография; [под ред. Е.Е. Еникеева]. М.: Изд. Интернаука, 2018. Т. 29.
С. 41–62.
Современный этап развития общества и, как следствие, эволюция научных подходов к изучению сложных больших систем, не поддающихся строгой формализации, характеризуется отказом от элементарного и ограниченного бинарного подхода и переходом к непрерывной (многозначной) логике, позволяющей объектам присутствовать в различных множествах с некоторой степенью принадлежности.
Таким образом, прогресс научного познания позволяет выполнить строгую математическую формализацию и использовать возможности аппарата принятия решений в нечетких условиях для исследования и управления процессами и системами при неопределённостях, обусловленных неполнотой и неточностью используемой исходной информации, данных о текущем состоянии системы и операторе ее перехода в следующее эволюционное состояние.
В настоящее время методология нечеткого моделирования находит применение в различных предметных областях: в образовании [1], медицине [2], экономике [3] и многих других. Целью настоящего исследования является разработка методологии и исследование модели выбора бизнес-системы в достаточно универсальной постановке.
Материалы и методы исследования
Рассмотрим задачу выбора бизнес-системы [3] в нечеткой постановке.
Пусть M, N и O – конечные четкие множества:
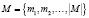
– список объектов для строительства;
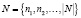
– список бизнес-систем;
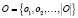
– список критериев (характеристик) для оценки надежности бизнес-систем.
Тогда нечеткая модель выбора бизнес-системы может быть определена как нечеткое реляционное уравнение
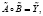
(1)
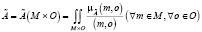
;
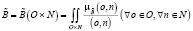
;
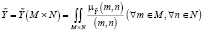
– искомое соответствие.
Очевидно, функция принадлежности практически может быть представлена в виде
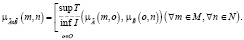
(2)
Формулы для нахождения решения задачи (2) при использовании наиболее известных треугольных норм T и индуцированных этими нормами импликаторов I [4] приведены в табл. 1.
Формулы для нахождения решения задачи
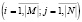
Решение
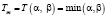
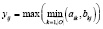
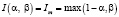
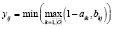 ;
; 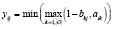
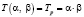
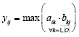
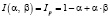
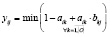 ;
; 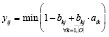
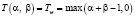
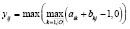
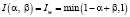
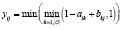 ;
; 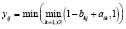
Представление прямой задачи (1) в виде (2) позволяет в простейшем случае при использовании стандартных треугольных норм и индуцированных ими импликаторов найти решения по одной из формул, приведенных в табл. 1.
Очевидно, выбор соответствующей импликации определяется спецификой решения прикладной задачи из исследуемой предметной области.
На рис. 1 приведены примеры графиков функций принадлежности и треугольной нормы, в виде логического произведения, и индуцированных ей двух импликаторов.
Рис. 2 иллюстрирует применение к аналогичным функциям принадлежности двух нечетких множеств треугольной нормы в виде алгебраического произведения.
На рис. 3 изображены рассматриваемые функции принадлежности, а также результаты применения к ним нормы в виде граничного произведения и соответствующих ему простейших импликаторов.
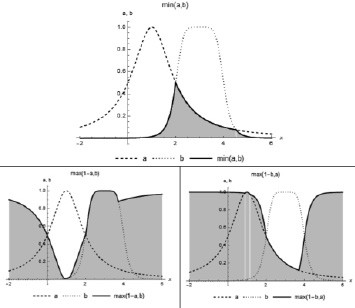
Рис. 1. Логическое произведение и индуцированные импликаторы
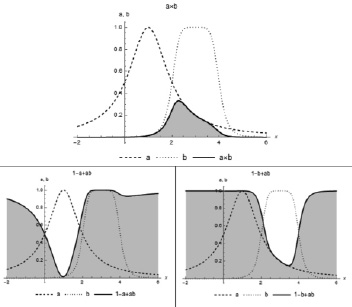
Рис. 2. Алгебраическое произведение и индуцированные импликаторы
Следует отметить, что при использовании логического произведения результат импликации остается слабо чувствительным к малым значениям функций принадлежности (в отличие от представленных на рис. 2 и 3), что может ограничить его применение в системах, например, обеспечения безопасности техногенных систем.
Решение обратной задачи принципиально сложнее, более того, множество решений может быть пусто. В этом случае решение обратной задачи можно свести к конечной проблеме оптимизации.
Пусть необходимо решить левую обратную задачу вида
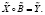
В этом случае формулируется соответствующая экстремальная задача:
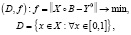
(3)
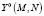
где – матричное представление наблюдаемого соответствия.
Решение этой задачи позволяет найти искомое нечеткое соответствие, которое в наивысшей степени отвечает условию минимизации критерия оптимизации – нормы отклонения расчетных величин от наблюдаемых.
Результаты исследования и их обсуждение
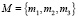 ;
; 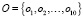 ;
; 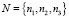
 ;
; 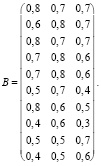
Решения прямой задачи (1) по формулам (2) при различных вариантах импликации представлены в табл. 2.
Варианты решения прямой задачи
Решение левой и правой задач
Источник: top-technologies.ru
НЕЧЕТКИЕ МОДЕЛИ В ПЛАНИРОВАНИИ ИНВЕСТИЦИЙ Текст научной статьи по специальности «Экономика и бизнес»
Аннотация научной статьи по экономике и бизнесу, автор научной работы — Федорова Наталья Васильевна, Акперов Имран Гурруевич
При планировании инвестиций условия дальнейшего ведения хозяйственной деятельности не всегда достоверно известны заранее. Социально-политические и природные факторы могут повлиять на величину инфляции, стоимость технических объектов и технологий, прибыль.
Это обусловливает актуальность исследований нечеткого моделирования планирования инвестиций . Одним из методов моделирования в условиях неопределенности является использование аппарата нечеткой логики Л. Заде. Целью данного исследования является применение методов нечеткой логики в планировании инвестиций . Задача исследования — разработка простейших S-образных моделей, отражающих влияние различных факторов на принятие решения об инвестировании . Ранее в подобных задачах, как правило, рассматривались треугольные или трапециевидные модели, что обусловливает новизну предлагаемого исследования. В результате исследования построен ряд нормализованных S-образных моделей (простейшая базовая, с поправочными коэффициентами, с долговыми обязательствами, с отложенным началом реализации, дополнительными поступлениями и инфляцией), которые наглядно показывают влияние отдельных факторов на принятие решения об инвестировании (рост располагаемых денежных средств, долговые обязательства, дополнительные ежегодные поступления средств, инфляция, развитие технологий производства). Для простейшей базовой диаграммы приведен пример дефаззификации. Данные модели могут использоваться как основа для построения более сложных моделей, учитывающих комбинации влияющих факторов.
i Надоели баннеры? Вы всегда можете отключить рекламу.
Похожие темы научных работ по экономике и бизнесу , автор научной работы — Федорова Наталья Васильевна, Акперов Имран Гурруевич
Мягкие вычисления как путь к преодолению НЕ-факторов в задачах оценки жизнеспособности проектов
Принятие решений по инвестированию ИТ-инноваций на основе нечеткой экспертной информации
ДИНАМИЧЕСКАЯ МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ ЛЕСОТРАНСПОРТНЫХ СИСТЕМ
Модель поддержки принятия решенияпри планировании проекта внедрения кис на основе нечетких множестввторого порядка
Нечетко-множественное моделирование в оценке эффективности технологических инноваций: актуальные методы и инструментальные средства
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
i Надоели баннеры? Вы всегда можете отключить рекламу.
FUZZY MODELS IN INVESTMENT PLANNING
When planning investments, the conditions for further business activities are not always reliably known in advance. Socio-political and natural factors can affect to the amount of inflation, cost of technical facilities and technologies, and profits. All these factors make studying fuzzy modeling of investment planning very important. One of the modeling methods under uncertainty conditions is using L. Zadeh apparatus of fuzzy logic. The purpose of the study is to apply fuzzy logic methods to investment planning.
The task of the study is to develop the elementary S-shaped models that show the influence of different factors on the decision to invest. Previously, in similar problems there were considered the triangular or trapezoidal models, which defines the novelty of the proposed study. As a result of the study, a number of normalized S-shaped models were built (the simplest basic, with adjustment factors, with debt obligations, with a delayed start of implementation, additional revenues and inflation), which clearly show the individual factors influencing the decision to invest (available funds growth, debt obligations, additional annual receipts of funds, inflation, development of production technologies). An example of defuzzification is given for the simplest basic diagram. The above models can be used as a basis for building more complex models that take into account the combinations of influencing factors.
Текст научной работы на тему «НЕЧЕТКИЕ МОДЕЛИ В ПЛАНИРОВАНИИ ИНВЕСТИЦИЙ»
Вестник АГТУ. Серия: Управление, вычислительная техника и информатика. 2022. Ля 3
ISSN2072-9502 (print), ISSN2224-9761 (online) VestnikASTU. Series: Management, computer science and informatics. 2022. № 3
_ISSN2072-9502 (print), ISSN2224-9761 (online)
УПРАВЛЕНИЕ В СОЦИАЛЬНЫХ И ЭКОНОМИЧЕСКИХ СИСТЕМАХ
SOCIAL AND ECONOMIC SYSTEMS MANAGEMENT
УДК 519.86:303.725.23:338.22.021.4 https://doi.org/10.24143/2072-9502-2022-3-61-70
Нечеткие модели в планировании инвестиций
Наталья Васильевна ФедороваИмран Гурруевич Акперов
Аннотация. При планировании инвестиций условия дальнейшего ведения хозяйственной деятельности не всегда достоверно известны заранее. Социально-политические и природные факторы могут повлиять на величину инфляции, стоимость технических объектов и технологий, прибыль. Это обусловливает актуальность исследований нечеткого моделирования планирования инвестиций.
Одним из методов моделирования в условиях неопределенности является использование аппарата нечеткой логики Л. Заде. Целью данного исследования является применение методов нечеткой логики в планировании инвестиций. Задача исследования — разработка простейших ¿’-образных моделей, отражающих влияние различных факторов на принятие решения об инвестировании.
Ранее в подобных задачах, как правило, рассматривались треугольные или трапециевидные модели, что обусловливает новизну предлагаемого исследования. В результате исследования построен ряд нормализованных ¿-образных моделей (простейшая базовая, с поправочными коэффициентами, с долговыми обязательствами, с отложенным началом реализации, дополнительными поступлениями и инфляцией), которые наглядно показывают влияние отдельных факторов на принятие решения об инвестировании (рост располагаемых денежных средств, долговые обязательства, дополнительные ежегодные поступления средств, инфляция, развитие технологий производства). Для простейшей базовой диаграммы приведен пример дефаззификации. Данные модели могут использоваться как основа для построения более сложных моделей, учитывающих комбинации влияющих факторов.
Ключевые слова: инвестирование, планирование инвестиций, моделирование, нечеткая логика, фаззифика-ция, функция принадлежности
Для цитирования: Федорова Н. В., Акперов И. Г. Нечеткие модели в планировании инвестиций // Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика. 2022. № 3. С. 61-70. https://doi.org/10.24143/2072-9502-2022-3-61-70.
Fuzzy models in investment planning
Natalia V. FedorovaM, Imran G. Akperov
Abstract. When planning investments, the conditions for further business activities are not always reliably known in advance. Socio-political and natural factors can affect to the amount of inflation, cost of technical facilities and
technologies, and profits. All these factors make studying fuzzy modeling of investment planning very important. One of the modeling methods under uncertainty conditions is using L. Zadeh apparatus of fuzzy logic. The purpose of the study is to apply fuzzy logic methods to investment planning. The task of the study is to develop the elementary ¿’-shaped models that show the influence of different factors on the decision to invest. Previously, in similar problems there were considered the triangular or trapezoidal models, which defines the novelty of the proposed study.
As a result of the study, a number of normalized ¿-shaped models were built (the simplest basic, with adjustment factors, with debt obligations, with a delayed start of implementation, additional revenues and inflation), which clearly show the individual factors influencing the decision to invest (available funds growth, debt obligations, additional annual receipts of funds, inflation, development of production technologies). An example of defuzzification is given for the simplest basic diagram. The above models can be used as a basis for building more complex models that take into account the combinations of influencing factors.
Keywords: investment, investment planning, modeling, fuzzy logic, fuzzification, membership function
For citation: Fedorova N. V., Akperov I. G. Fuzzy models in investment planning. Vestnik of Astrakhan State Technical University. Series: Management, Computer Science and Informatics. 2022;3:61-70. (In Russ.) https://doi.org/10.24143/2072-9502-2022-3-61-70.
Инвестирование в проектирование и строительство технических объектов — одна из форм бизнеса, целью которого является получение прибыли. При математическом моделировании инвестирования ставятся задачи: минимизация срока окупаемости, максимизация прибыли, оптимизация платежей.
Задача может иметь внешние ограничения, связанные с условиями реализации проекта, и внутренние ограничения, обусловленные особенностями проекта. Внешними ограничениями могут являться ограниченность располагаемых финансовых средств; периодичность поступления финансовых средств, которые планируется инвестировать; возможности и условия долговых обязательств; инфляция; ограниченность времени ожидания реализации проекта; риски различной природы и др. Внутренние ограничения обусловлены структурой проекта, возможностью разбиения его на части (подсистемы), взаимосвязями между частями, очередностью ввода частей в действие. Одним из вариантов стратегии инвестирования в условиях ограничений является разбиение проекта на независимые части и реализация его по частям. Проведем моделирование подобной стратегии с применением методов нечеткой логики Л. Заде [1, 2].
Постановка задачи исследования
Ставится задача разработки нечетких моделей фаззификации процесса планирования инвестиций при возможности разбиения основного проекта на части и с учетом некоторых внешних ограничений.
Предлагаемый метод исследования включает построение 51-диаграмм планирования инвестиций.
Ранее используемые методы были основаны на использовании четких аналитических моделей [3, 4]. При использовании же нечетких моделей преимущество отдавалось треугольным, трапециевидным или иным, предусматривающим выделение, как правило, трех и более опорных состояний
(например, расходы низкие/средние/высокие) [5, 6]. Достоинствами аналитических методов являются представление модели проблемы в виде системы равенств и неравенств и возможность аналитического исследования выявленных закономерностей. Недостатки аналитических методов — усложнение модели при необходимости учета различных факторов, не всегда достоверно известный характер влияния фактора. При использовании нечеткой логики достоинством является возможность исследования в условиях нечетко заданных ограничений. Но выделение опорных состояний основано на анализе совокупности экспертных оценок, а процесс дефаз-зификации является достаточно сложным, что составляет недостатки данного метода.
Достоинствами предлагаемого метода исследования являются его простота, возможность работы с нечеткими ограничениями и снижение необходимости в экспертной оценке. Стоимость проекта и отдельных его частей определяются по технико-экономическим показателям. Поправочные коэффициенты могут быть оценены на основе анализа статистических данных.
Дополнительные денежные поступления планируются на основании финансового анализа. Снижается влияние субъективизма эксперта. Теоретическая значимость и научная новизна предлагаемого метода заключаются в разработке нового подхода к моделированию инвестиционной деятельности в условиях нечетко заданных ограничений. Данный метод может использоваться как в практике моделирования инвестиционных процессов, так и в учебной деятельности для наглядного представления влияния различных факторов на процесс принятия решения в планировании инвестиций, что обусловливает его практическую значимость.
Методы нечеткой логики
Нечеткое подмножество А универсального множества Е, элементы которого удовлетворяют свойству Я, определяется как множество упорядо-
функция принадлежности, указывающая степень соответствия элемента х подмножеству А. Значение (~ 0 означает отсутствие принадлежности к множеству, = 1 — полную принадлежность.
Некоторые операции с нечеткими множествами:
— более или менее А: ^1а(х) ;
— А или В (сумма, объединение, ®): тах(ц/)(х), Ых));
— А и В (произведение, пересечение, ): ппп(ц^(х), Цй(х)).
Получение результата производится в три этапа: фаззификация (переход к нечетким объектам) — нечеткий вывод — дефаззификация (возвращение к четким понятиям, численным данным и т. п.). Применяют модели фаззификации Z-oбpaзныe, ^-образные, треугольные, трапециевидные и др. [7-10]. В данной работе представлены некоторые простейшие ^-образные модели фаззификации, применимые в планировании инвестиций.
Основные понятия и соотношения инвестирования Рассмотрим проект РЯ, который можно разбить на п независимых частей. Введем в рассмотрение параметры и обозначения: Я, — стоимость проекта, минимальная и максимальная стоимости частей проекта соответственно; Ш — объем собственных финансовых средств инвестора на начало инвестирования; — суммарный объем располагаемых финансовых средств; РУ — ежегодные дополнительные поступления средств от иных источников, не обремененные долгом; РР — прибыль от реализации проекта; О — средства, взятые в долг на реализацию проекта (в том числе, после окончания реализации проекта до завершения срока контроля); ОУ — ежегодные платежи по долговым обязательствам, связанным с проектом; ОР — ежегодные инвестиции в проект; — ежегодные платежи инвестора, не связанные с проектом и с долговыми обязательствами по проекту; — суммарные ежегодные платежи, связанные с проектом; — совокупные суммарные ежегодные платежи; К1 — инфляционный поправочный коэффициент, К1 > 1; КТ — технологический поправочный коэффициент, 0 < КТ < 1; ТР — срок реализации проекта, лет; ТО — отсрочка начала реализации проекта, лет; ТЯ — суммарный срок контроля состояния проекта, лет; i — год от начала реализации проекта (части проекта); 7 — год от принятия решения о реализации проекта (части проекта).
Полагаем, что решение о реализации проекта принимается при 7=1.
Состояние проекта контролируется до окончания долговых платежей, связанных с проектом.
Введенные в рассмотрение параметры связаны соотношениями:
>Smin i «S’max — S iSmin • П < S < ‘ Tl
i=j- TO приj> TO, i не определено при j < TO;
DP(j) = 0 при j < TO или при j >TO + TP;
PP(j) > 0 при TO + TP TO + TP;
с другой стороны, с учетом прошлого года RS(j) = RS(j -1) + PY(j) + D(j) + PP(j) — DS(f); 7 > 1.
Положительное решение о финансировании проекта или его части принимается, если на момент принятия решения стоимость всех платежей не превышает стоимости располагаемых денежных средств, с учетом разбивки реализации по годам, т. е.
Контроль реализации проекта прекращается после TS лет, если DY(j) > 0 при 1 < j < TS и DY(TS+ 1) = 0.
Модели планирования инвестиций
1. Простейшая базовая модель.
Постановка задачи. Планируется принять решение о реализации проекта в текущем году за счет имеющихся в наличии средств, без долгов и дополнительных поступлений. Полагаем, что прибыль также будет получена к концу текущего года.
Графическая модель проблемы представлена на рис. 1.
Низкий уровень принадлежности
— Высокий уровень принадлежности
Располагаемые финансовые средства, у. е.
Рис. 1. Простейшая ¿-диаграмма планирования инвестиций и ее дефаззификация: RSqi, RS02 — промежуточные значения
Fig. 1. Elementary ¿-diagram of investment planning and its defuzzification: RS0], RS02 -.intermediate values
Принятые значения функции принадлежности: — 0
—/= 1 — однозначно выгодно принять решение ние о реализации проекта, возможна реализация о начале реализации проекта или любой его части; части с минимальной стоимостью;
Модель проблемы можно описать соотношениями
Аналитически модель проблемы выражается формулами
планирования. Введем два значения располагаемых показателя: финансовых средств: RS
А = = 0,25(5тах-5тш)+0,75(5-5шах) = 0,25 (35—5^0;
А1 = [ /(ЯБ)с1ЯБ = 0,25(ЯБ 01 — / ^^тах —
А2= Г f(RS)dRS = 0,25(ш,) + 0,5(Д5о2 -5тах)+0,25(Д5о2
= 0,25(2*5 02— 5тах — ^тш)+0,25(^02 — 5тах^ —
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Тогда полагаем четкой вероятностью принятия личину Р01 = А1 / А, а в случае располагаемых положительного решения об инвестировании средств RSo2 — величину Р02 = А2 / А. в проект в случае располагаемых средств RSo] ве-
Выводы по текущему разделу. Рекомендуется приступать к реализации проекта, если располагаемые финансовые средства не менее максимальной стоимости части проекта.
2. Простейшая модель с учетом поправочных коэффициентов.
Постановка задачи. Планируется принять решение о реализации проекта в следующем году за счет имеющихся в наличии средств, без долгов и дополнительных поступлений. Стоимость проекта и его частей к началу следующего года может снизиться за счет развития технологий или увеличиться вследствие инфляции. Полагаем, что прибыль также будет получена к концу следующего года.
Графическая модель проблемы представлена на рис. 2, где введены новые параметры: -,
£т1-п- минимальная и средне-минимальная стоимости части проекта с учетом улучшения технологии, = №шп — йшп- -) / 2; йшП++, йшп+ — минимальная и средне-минимальная стоимости части проекта с учетом инфляции, £т1-п+ = (£т1П++ — £т1-п) / 2; ¿>тах— максимальная и средне-максималь-ная стоимости части проекта с учетом улучшения технологии, £тах- = (£тах — £тах-—) / 2; £тах++, £тах+ -максимальная и средне-максимальная стоимости части проекта с учетом инфляции, £тах+ = (£тах++ -^тах) / 2; £—, £++, — минимальная и средне-минимальная стоимости проекта с учетом улучшения технологии, максимальная и средне-максимальная стоимости проекта с учетом инфляции стоимости проекта соответственно, £- = (£- £—) / 2, 5+ = = (£++ /2.
Располагаемые финансовые средства, у. е.
Рис. 2. Диаграмма планирования с интервальными поправочными коэффициентами Fig. 2. Diagram of planning with interval adjustment factors
Ropt, Rpes, Rb, Ru — суммарный объем располагае- Аналитически модель проблемы выражается мых финансовых средств при оптимистическом, формулами: пессимистическом, базовом и итоговом сценариях — для базового сценария соответственно, в простейшем случае Ropt = Rpes = = Rb = Rit = RS.
/Ч Г Rb ~ Smax л 0 ^ „
для оптимистического сценария
Источник: cyberleninka.ru
