Есть три вида средних, и они могут выражаться разными числами. Поэтому те, кто всерьез занимается статистикой, избегают слова «среднее», отдавая предпочтение более точным терминам: среднее арифметическое, медиана или мода. Иногда все эти величины совпадают, но чаще они различаются.
Чаще других встречается среднее арифметическое; оно равно сумме всех данных, поделенной на их количество. Медиана — это число в середине упорядоченного набора чисел (статистики называют его выборкой): половина данных находится ниже этого значения, а половина выше. Мода — цифра, которая встречается чаще других.
Представим себе комнату, в которой находятся девять человек; состояние восьмерых из них равно примерно $100 тысяч, а один находится на грани банкротства, его долг равен $500 тысячам. Вот что у нас получится:
- Человек 1: –500 тыс. долл.
- Человек 2: 96 тыс. долл.
- Человек 3: 97 тыс. долл.
- Человек 4: 99 тыс. долл.
- Человек 5: 100 тыс. долл.
- Человек 6: 101 тыс. долл.
- Человек 7: 101 тыс. долл.
- Человек 8: 101 тыс. долл.
- Человек 9: 104 тыс. долл.
Теперь складываем все показатели и получаем общую сумму в $299 тысяч. Среднее арифметическое равно $33 222. Как видим, это не лучший способ охарактеризовать данные о присутствующих.
5 принципов как определить сколько платить сотрудникам / Управление персоналом 16+
И медиана, и мода в этом примере оказываются гораздо показательнее. Медиана равна $100 тысячам: четверо зарабатывают меньше этой суммы, а четверо — больше. Мода равна $101 тысяче — это то число, которое появляется чаще других.
Бимодальное распределение

Если вы работаете со средними, остерегайтесь бимодального распределения. Во многих наборах данных — биологических, физических, социальных — у распределения может быть два или больше пиков.
Например, подобный график может отображать сумму, потраченную на обеды в неделю (ось X), и количество людей, потративших такую сумму (ось Y). Представьте, что вы изучали две группы людей: детей (левый горб) — они покупают школьные обеды — и руководителей компаний (правый горб) — они ходят в дорогие рестораны.
Среднее арифметическое и медиана в данном случае — это числа где-то между этими двумя горбами, и они ничего не скажут о том, что происходит на самом деле, — ведь во многих случаях среднее арифметическое и медиана отражают ту сумму, которую никто не тратит. Подобный график говорит лишь о том, что в вашем примере имеет место неоднородность — вы сравниваете яблоки с апельсинами. В таком случае лучше сразу сказать, что вы имеете дело с бимодальным распределением, и сообщить о двух модах. А еще лучше разделить группу на две подгруппы и собрать статистические данные для каждой.
Экологическая ошибка
Будьте осторожны, когда будете делать выводы об отдельных людях и о группах, основываясь на средних данных. Тут легко наткнуться на экологическую ошибку.
Экологическая ошибка возникает, если мы делаем выводы об отдельном элементе, основываясь на совокупных данных. Представьте себе два маленьких городка, в каждом из которых живет всего по сотне человек. Девяносто девять жителей города А зарабатывают по $80 тысяч в год, а на земле одной женщины было найдено месторождение нефти, и теперь она получает $5 миллионов в год. В городе Б живут 50 человек, которые зарабатывают по $100 тысяч в год, а также 50 человек, которые получают по $140 тысяч. Средний арифметический доход в городе А составляет $129 тысяч, а в городе Б — $120 тысяч. И хотя средняя величина доходов города А больше, в 99 случаях из 100 доход любого жителя города Б, которого вы выберете наугад, будет выше дохода любого случайно выбранного жителя города А.
Мода, размах, среднее арифметическое, медиана
Экологическую ошибку совершают те, кто считает, что если выбрать наугад человека из группы с более высоким средним доходом, то и у него доход будет выше.
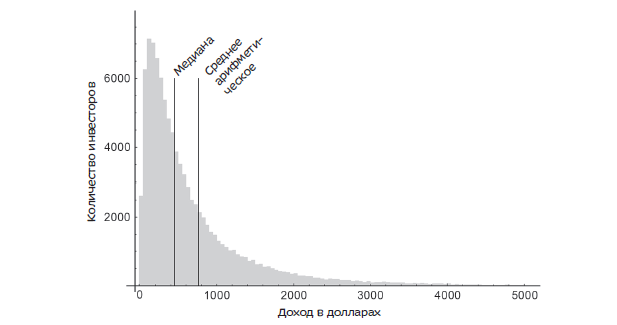
Средний инвестор не получает средний доход
Посещает ли средний студент колледжа колледж среднего размера, растет ли среднее дерево в среднем лесу и получает ли средний инвестор средний доход? Нет.
В одном исследовании средний доход от инвестиции 100 долларов на срок 30 лет составил 760 долларов, или 7% в год. Звучит неплохо. Но эта статистика не показывает, что 9% инвесторов потеряли деньги, а огромному числу инвесторов, 69%, не удалось достигнуть показателя среднего дохода. Так случилось потому, что среднее арифметическое было смещено из-за нескольких человек, заработавших больше среднего.
Будьте осторожны со средними, а также с тем, как их интерпретируют. Усредняя данные по выборкам из несопоставимых совокупностей, игнорируя разброс значений, допуская экологические ошибки мы видим мир искаженным и принимаем неверные решения.
Материалы по теме:
Источник: rb.ru
Средняя величина в бизнесе


Применение средних величин в профессиональной деятельности менеджера по продажам
Качарава А.С. 1
1 Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж» (ОГБПОУ «КТЭК»)
Холинова О.А. 1
1 Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж» (ОГБПОУ «КТЭК»)

Автор работы награжден дипломом победителя III степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Актуальность. Основой работы менеджера является принятие управленческих решений. Для этого весьма часто прибегают к использованию методов математической статистики.
В условиях широкого применения методов современной математики во всех областях научных исследований, фундаментальных и прикладных, а также в решении ряда практических проблем общественной жизни внимание уделяется математической статистике. Предлагая свою математическую технику применительно к вероятностного характера изучаемых явлений и процессов, математическая статистика становится методом по отношению к специальным наук, в которых она применяется. Её математический аппарат плодотворно используется при изучении явлений и процессов, происходящих в жизни общества.
Существенную роль в обосновании управленческих решений играют методы математической статистики. Математическая статистика находит широкое применение в экономике различных отраслей народного хозяйства, биологии, физике, химии, медицине и др. На основе ее методов можно решать и многие аналитические задач в области экономики. В частности, количественные характеристики, полученные в результате математико-статистического анализа, позволяют иметь более глубокое представление о характере причинно-следственных связей явлений, а также получить устойчивые надежные параметры для осуществления экономических расчетов и особенно с целью прогнозирования.
Большим шагом в развитии статистической науки послужило применение экономико-математических методов в анализе социально-экономических явлений.
Развитие статистической науки, расширение сферы применения практических статистических исследований, ее активное участие в механизме управления экономикой привели к изменению содержания самого понятия «статистика».
На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления (характеристика государства: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда). Системные средние могут характеризовать как пространственные или объектные системы, существующие одномоментно (государство, отрасль, регион, планета Земля и т.д.), так и динамические системы, протяжённые во времени (год, десятилетие, сезон и т.д.).
В экономической практике используется широкий круг показателей, вычисленный в виде средних величин.
Главное значение средних состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.
Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности.
Однако неправильно сводить роль средних величин только к характеристике типичных значений признаков в однородных по данному признаку совокупностях. На практике значительно чаще современная статистика использует средние величины, обобщающие явно однородные явления.
В условиях рынка предприятие является главным объектом хозяйствования, независимым товаропроизводителем, экономическое пространство для которого практически неограниченно, но всецело зависит от умения работать безубыточно, адаптируясь к условиям изменяющейся экономической среды. Производственные показатели характеризуют эффективность деятельности предприятия.
Обеспечение качества систем управления требует широкого применения статистических методов. Статистические методы, позволяют установить закономерности и причины изменений явлений и процессов, имеющих место на предприятии или в организации, являются мощным инструментом обоснования принимаемых решений и оценки их эффективности. При анализе показателей внешней торговли наряду с применением абсолютных и относительных величин широкое распространение получили средние величины. Круг задач, решаемых с применением средних величин достаточно широк. В таможенной статистике внешней торговли средние величины характеризуют:
уровень цен на товары, обращающиеся во внешнеторговом обороте;
уровень стоимостного и количественного объёма экспорта и импорта товаров в общем и в разрезе товарных групп, товарных позиций, отдельных товаров и стран;
средние темпы роста товарооборота, экспорта, импорта.
Актуальность темы заключается в том, что область применения и использования средних величин в статистике довольно широка.
Цель: ознакомление с применением средних величин в статистике.
В связи с заданной целью были поставлены следующие задачи:
охарактеризовать средние величины в экономическом анализе;
раскрыть виды средних величин;
Предмет исследования: применение средних величин.
Объект исследования: средние величины в статистике.
1.История развития средних величин
История практического применения средних насчитывает десятки столетий. Основная цель расчета средней состояла в изучении пропорций между величинами. Значимость расчетов средних величин возросла в связи с развитием теории вероятностей и математической статистики. Решение многих теоретических и практических задач было бы невозможно без расчетов средней и оценки колеблемости индивидуальных значений признака.
Ученые разных направлений стремились дать определение средней. Например, выдающийся французский математик О.Л.Коши (1789 — 1857) считал, что средней нескольких величин является новая величина, заключающаяся между наименьшей и наибольшей из рассматриваемых величин.
Однако создателем теории средних следует считать бельгийского статистика А. Кетле (1796 — 1874). Им предпринята попытка определить природу средних величин и закономерностей, в них проявляющихся. Согласно Кетле, постоянные причины действуют одинаково (постоянно) на каждое изучаемое явление. Именно они делают эти явления похожими друг на друга, создают общее для всех их закономерности.
Следствием учения А. Кетле об общих и индивидуальных причинах явилось выделения средних величин в качестве основного приема статистического анализа. Он подчеркивал, что статистические средние представляют собой не просто меру математического измерения, а категорию объективной действительности. Типическую, реально существующую среднюю он отождествлял с истинной величиной, отклонения от которой могут быть только случайными.
Ярким выражением изложенного взгляда на среднюю является его теория «среднего человека», т.е. человека среднего роста, веса, силы, среднего объема грудной клетки, емкости легких, средней остроты зрения и обычным цветом лица. Средние характеризуют «истинный» тип человека, все отклонения от этого типа указывают на уродливость или болезнь.
Взгляды А.Кетле получили дальнейшее развитие в работах немецкого статистика В.Лексиса (1837 — 1914).
Другая разновидность идеалистической теории средних основана на философии махизма. Ее основатель английский статистик А. Боули (1869 — 1957). В средних он видел способ наиболее простого описания количественных характеристик явления. Определяя значение средних или, как он выражается, «их функцию», Боули на первый план выдвигает махистский принцип мышлений.
Так, он писал, что функция средних ясна: она заключается в том, чтобы выражать сложную группу при помощи немногих простых чисел. Ум не в состоянии сразу охватить величины миллионов статистических данных, они должны быть сгруппированы, упрощены, приведены к средним.
Последователем А.Кетле был и итальянский статистик К.Джини (1884-1965), автор крупной монографии «Средние величины». К.Джини подверг критике определение средней, данное советским статистиком А.Я. Боярским, и сформулировал свое: «Средняя нескольких величин является результатом действий, выполняемых по определенному правилу над данными величинами, и представляет собой либо одну из данных величин, которая не больше и не меньше всех остальных (средняя действительная или эффективная), либо какую-либо новую величину, промежуточную между наименьшей и наибольшей из данных величин (счетная средняя)».
2.Понятие средней величины и принципы применения средних величин.
Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел [2] . Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.
Средняя величина – это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
Средняя применяется в статистических исследованиях для оценки сложившегося уровня явления, для сравнения между собой нескольких совокупностей по одному и тому же признаку, для исследования динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений. Например, на производство одного и того же количества товара определенного вида и качества разные производители (заводы, фирмы) затрачивают неодинаковое количество труда и материальных ресурсов. Но рынок осредняет эти затраты, и стоимость товара определяется средним расходом ресурсов на производство. С помощью статистических методов решаются многие задачи организации и планирования на производстве, а также иных прикладных экономических задач [1] .
Средние широко применяются в различных плановых, прогнозных, финансовых расчетах.
Главное значение средних величин состоит в их обобщающей функции, т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.
Общие принципы применения средних величин:
1) необходим обоснованный выбор единицы совокупности, для которой рассчитывается среднее значение;
2) при расчете средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные;
3) средние величины должны рассчитываться, прежде всего, по однородным совокупностям. Качественно однородные совокупности позволяют получить метод группировок, который предполагает расчет не только среднего значения, но и системы обобщающих показателей;
4) общие средние (средние для всей совокупности) должны подкрепляться групповыми средними. Например, анализ динамики урожайности отдельной сельскохозяйственной культуры показывает общее по республике снижение урожайности. Однако известно, что урожайность этой культуры зависит от почвенных, климатических, территориальных, экономических и других условий конкретного сельскохозяйственного года и различна в отдельных регионах. Сгруппировав регионы по уровню урожайности каждого года и проанализировав динамику групповых средних, можно обнаружить, что в отдельных группах регионов средняя урожайность либо не изменилась, либо даже возросла, но одновременно возросли удельный вес или число районов с более низкой урожайностью этой сельскохозяйственной культуры. Очевидно, что анализ факторов динамики средних групповых позволяет более полно отразить закономерности изменения урожайности по сравнению с динамикой общего среднего результата.
3. Виды средних величин.
Все средние величины делятся на два больших класса:
1) степенные средние; к ним относятся такие известные и часто применяемые виды, как средняя арифметическая величина, средняя квадратическая и средняя геометрическая;
2) структурные средние величины, в качестве которых рассматриваются мода и медиана [3] .
Кроме того, в статистике существует и иная классификация средних величин:
1.По наличию признака-веса:
а) невзвешенная средняя величина;
б) взвешенная средняя величина.
2. По форме расчета:
а) средняя арифметическая величина;
б) средняя гармоническая величина;
в) средняя геометрическая величина;
г) средняя квадратическая, кубическая и т.д. величины.
3. По охвату совокупности:
а) групповая средняя величина;
б) общая средняя величина.
Средние величины различаются в зависимости от учета признаков, влияющих на осредняемую величину:
Если средняя величина рассчитывается для признака, без учета влияния на него каких-либо других признаков, то такая средняя величина называется средней невзвешенной или простой средней.
Если имеются сведения о влиянии на осредняемый признак некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная.
3.1.Степенные средние величины.
По форме расчета выделяют несколько видов средних величин, которые образованы из единой степенной средней величины. Степенная средняя величина имеет форму:
k – показатель степени средней;
x – текущее значение (вариант) осредняемого признака;
i –i-тый элемент совокупности;
n – число наблюдений (число единиц совокупности).
При разных показателях степени k получаем, соответственно, различные по форме средние величины. (Табл.1):
средней величины (k)
Название
средней
Источник: school-science.ru
Средняя величина в бизнесе

31 Янв Средние продажи и скорость продаж: как рассчитать
Posted at 11:50h in Статьи by Olga
Для того, чтобы определить сколько заказывать товара у поставщика или насколько необходимо пополнить остатки с центрального склада, в первую очередь нужно понимать сколько в будущем будет продаваться товара. Будущая потребность в товаре определяется разными методами. Ее можно определять по плану продаж, прогнозу спроса, заказам клиента, также можно определять экспертным методом. Чаще всего прогнозируются будущие продажи с помощью расчета средних продаж.
Когда мы говорим о средних продажах, то чаще всего речь идет о расчете среднего арифметического значения продаж за определенный период.
Средняя арифметическая продажа
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции. Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами
Средняя арифметическая продажа вычисляется по формуле:

Где x – значение продаж в каждом периоде,
n – количество периодов (дней, недель, месяцев).
Для того чтобы рассчитать среднюю арифметическую продажу за период, нужно взять продажи за период и разделить на количество периодов. К примеру, если мы считаем среднюю продажу за неделю, то мы берем продажи за неделю и делим на 7 дней.
В Excel есть встроенная функция для определения среднего арифметического, называется она СРЗНАЧ. Эта функция возвращает среднее значение (среднее арифметическое) аргументов. Например, если диапазон A1:A20 содержит числа, формула =СРЗНАЧ(A1:A20) возвращает среднее значение этих чисел.
Синтаксис этой функции
Число1. Обязательный аргумент. Первое число, ссылка на ячейку или диапазон, для которого требуется вычислить среднее значение.
Число2, … Необязательный аргумент. Дополнительные числа, ссылки на ячейки или диапазоны, для которых требуется вычислить среднее значение. Аргументов может быть не более 255.
В Excel есть также функции СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИМН, с помощью которых можно вычислить среднее только для тех значений, которые удовлетворяют определенным критериям
Средняя арифметическая взвешенная продажа
Средняя арифметическая величина используется в виде простой средней и взвешенной средней.
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она рассчитывается по формуле:

![]()
,
Где x — значение продаж в каждом периоде,
w – величина веса.
Подробнее о расчете средневзвешенной можно прочитать в моей статье «Расчет средневзвешенной продажи»
Скорость продаж
При расчете средних продаж, мы можем столкнуться с тем, что не всегда товар был на складе. Если мы будем рассчитывать среднюю продажу и не учитывать дни, когда товара не было на складе и на основании этой средней продажи будем рассчитывать пополнение запаса, то в результате товара опять не будет хватать. Мы заранее рассчитаем такое пополнение запаса, при котором товара опять не хватит. Очевидно, что нам необходимо понимать какие были бы продажи, если бы не было дефицита.
Здесь нам может помочь показатель — скорость продаж. Он показывает продажи в среднем за один день и в те дни, когда товар был на складе, или по товару было движение за этот день. Почему важно учесть еще движение в течение дня? Если товар в течение дня придет и уйдет, на начало и конец дня будут нулевые значения остатка, а значит этот день не попадет в расчет, хотя продажи фактически были и остаток был в течение дня.
Для расчета данного показателя необходимо посчитать количество дней, когда товар был на складе, т.е. остаток больший нуля, или по товару было движение за этот день. Далее необходимо разделить продажи за период на количество этих дней.

В таблице представлены данные о продажах и об остатках по товару.
За 12 дней продано всего 121 шт.
Средняя арифметическая продажа равна 10,1 шт.
Обратите внимание, что два дня товара не было на остатках – 8 и 9 марта.
Если мы уберем из расчета эти дни, то скорость продаж будет равна 12,1 шт. В данном случае разница может показаться незначительной, но если мы заказываем на 20 дней. то разница в пополнении будет в 20 штук — эта разница существенная.
Очевидно, что вручную мы можем посчитать несколько позиций, но если позиций много, то расчеты скорости продаж будут трудоемкими и займут много времени. Но данный алгоритм просто реализовать в 1С и уже далее использовать при заказе поставщику.
Примечание: Вы можете скачать таблицу Excel с примером расчета . Оставьте в форме свой электронный адрес и получите таблицу с примером.
Для тех, кто хочет быстро и качественно выполнять расчет заказа поставщикам, учитывая будущие продажи, срок выполнения заказа, периодичность размещения заказа, остатки на складе, остатки в пути я подготовила практический онлайн-курс “Управление запасами: Как рассчитать заказ поставщику без дефицита и неликвидов” .
Пройдите курс и получите готовые формулы и навыки для расчета заказа поставщикам!
Онлайн-курс — это 7 занятий в формате видеоуроков по 2-2,5 часа с домашними заданиями и примерами расчетов в Excel.
Источник: uppravuk.net
