Математическое моделирование позволяет до создания реальной системы (объекта) или возникновения реальной ситуации рассмотреть возможные режимы работы, выбрать оптимальные управляющие воздействия, составить объективный прогноз будущих состояний системы. Вычислительные эксперименты, проводимые на основе математических моделей, помогают увидеть за частным общее, развить универсальные методы анализа объектов различной физической природы, познать свойства изучаемых процессов и систем.
Наконец, математическое моделирование является основой интенсивно разрабатываемых автоматизированных систем проектирования, управления и обработки данных. Основная задача математического моделирования – выделение законов в природе, обществе и технике и запись их на языке математики. Например: 1) Зависимость между массой тела m, действующей на него силой F и ускорением его движения а записывается в форме 2-го закона Ньютона: F = m× a; 2) Зависимость между напряжением в электрической цепи U, ее сопротивлением R и силой тока I записывается в виде закона Ома: I = U/R. Существует множество определений математической модели. Приведем одно из них:
Математическое моделирование — Лекция 1 (09.02.07)
Рекомендуемые материалы
Маран Программная инженерия
Программная инженерия
Техническое задание
Инженерная графика
Курсовой проект по деталям машин под ключ в бауманке
Детали машин (ДМ)
11900 11111 руб.
КМ-3. Типовое задание к теме прямые измерения. Контрольная работа (ИЗ1) — любой вариант!
Метрология и информационно-измерительная техника
2790 2569 руб.
Математической моделью некоторого объекта, процесса или явления будем называть запись его свойств на формальном языке с целью получения нового знания (свойств) об изучаемом процессе путем применения формальных методов. Альтернативой формальному (математическому) подходу является экспериментальный подход. К его недостаткам можно отнести: 1) высокая стоимость подготовки и проведения экспериментов; 2) получение частного знания (знания о конкретном объекте исследования, а не о классе объектов). Например, пусть требуется определить воздействие х на некоторый процесс или объект, при котором его результирующая характеристика у имеет максимально возможное значение (Рис. 1.1).
 |

а б Рис. 1.1. На рис. 1.1. а) показан эмпирический (экспериментальный) подход к решению поставленной задачи, который состоит в экспериментальном определении значения параметра у для нескольких значений входного воздействия х. Среди них найдено наибольшее, и оно принимается за максимум.
Как видим из этого рисунка, возможно несколько значений воздействия х (х4 и х5), при которых у имеет наибольшее значение, но ни одно из них не является настоящим максимумом, который, возможно, лежит между ними. Математический подход (рис. 1.1. б) предполагает наличие математической модели процесса типа y = f(x).
Любой бизнес — это математическая модель. Евгений Черняк. Миллиарды / Billions
Взяв производную и приравняв ее к нулю, получим уравнение, решением которого является точное значение xmax , доставляющее максимум функции у. Схема применения математической модели при решении реальных задач имеет вид, показанный на рис. 1.2.
 |
Рис. 1.2 Модель сложного объекта (процесса, системы) не может быть простой. Из чего следует, что процесс использования математических моделей реальных систем является итерационным процессом, когда последовательно уточняется (дорабатывается) математическая модель и методы решения стоящих задач.
Важнейшей характеристикой моделей является их точность, адекватность действительности. При этом важно иметь в виду, что все модели представляют собой приближенное описание реальных объектов (процессов) и поэтому принципиально неточны.
Интегральная оценка модели может быть получена путем сравнения результатов моделирования и экспериментальных данных для конкретных объектов или режимов. Для оценки значимости совпадения или несовпадения модельных и экспериментальных результатов широко используются методы математической статистики. Вместе с тем не следует переоценивать результаты такой проверки. Хорошее совпадение модельных и экспериментальных данных, вообще говоря, не доказывает точности модели, а лишь подтверждают ее функциональную пригодность для моделирования. Всегда может быть предложена модель, обеспечивающая лучшее совпадение с экспериментом, но не лучшее описание моделируемого объекта или процесса.
1.2. Классификация математических моделей
Существует несколько схем классификации математических моделей. Все они достаточно условны. Одна из таких схем приведена на рис. 1.3.
| Математические модели | ||
| Аналитические | Имитационные | |
| Теоретические | Эмпирические | Теоретические |
| Линейные | Нелинейные | Нелинейные |
| Статические | Динамические | Динамические |
| Детермини-рованные | Стохастические | Детермини-рованные |
| Аналитически разрешимые | Численно разрешимые | Численно разрешимые |
Рис. 1.3 Все математические модели по использованному формальному языку можно разбить на аналитические и имитационные. Аналитические – модели, в которых используется стандартный математический язык. Имитационные – модели, в которых использован специальный язык моделирования или универсальный язык программирования.
Аналитические модели могут быть записаны в виде формул или уравнений. Если какой-либо процесс не может быть описан в виде аналитической модели, его описывают с помощью специального алгоритма или программы. Такая модель является имитационной. Аналитические модели в свою очередь разбиваются на теоретические и эмпирические модели.
Теоретические модели отражают реальные структуры и процессы в исследуемых объектах, то есть, опираются на теорию их работы. Эмпирические модели строятся на основе изучения реакций объекта на изменение условий окружающей среды.
При этом теория работы объекта не рассматривается, сам объект представляет собой так называемый «черный ящик», а модель – некоторую интерполяционную зависимость. Эмпирические модели могут быть построены на основе экспериментальных данных. Эти данные получают непосредственно на исследуемых объектах или с помощью их физических моделей.
По форме описания аналитические модели подразделяются на линейные и нелинейные. Если все входящие в модель величины не зависят от времени, то имеем статическую модель объекта или процесса, в противном случае получаем динамическую модель. В детерминированных моделях все взаимосвязи, переменные и константы заданы точно, что приводит к однозначному определению результирующей функции. Если часть или все параметры, входящие в модель по своей природе являются случайными величинами или случайными функциями, то модель относят к классу стохастических моделей.
В стохастических моделях задаются законы распределения случайных величин, что приводит к вероятностной оценке результирующей функции. Если аналитическое исследование может быть доведено до конца, модели называются аналитически разрешимыми. В противном случае говорят о численно разрешимых аналитических моделях.
Контрольные вопросы к лекции 1
1. Что позволяет осуществить математическое моделирование до создания реальной системы, объекта? 2. Что позволяют увидеть вычислительные эксперименты? 3. Сформулируйте основную задачу математического моделирования. 4. Дайте определение математической модели. 5. Какой подход решения научных задач является альтернативным математическому моделированию?
6. Перечислите основные недостатки экспериментального подхода. 7. Что является важнейшей характеристикой математической модели? 8. На какие два вида делятся математические модели? 9. Перечислите виды аналитических математических моделей. 10.
Дайте краткую характеристику видов моделей.
1.3. Геометрическое представление математических моделей

Геометрически математическая модель может быть представлена как некоторая поверхность отклика, соответствующая расположению точек W = W(x) в k-мерном факторном пространстве Х. Наглядно можно представить себе только одномерную и двухмерную поверхности отклика, причем в последнем случае удобно пользоваться топографическим способом изображения рельефа поверхности с помощью линий уровня (изолиний), построенных в двумерном факторном пространстве Х. (Рис. 1.4).
 |
Рис. 1.4 Область, в которой определена поверхность отклика, называется областью определения Х*.
Эта область составляет, как правило, лишь часть полного факторного пространства Х (Х* Ì Х) и выделяется с помощью ограничений, наложенных на управляющие переменные xi , записанных в виде равенств xi = Ci , i = 1,…, m; fj(x) = Cj , j = 1,…, l или неравенств xi min £ xi £ xi max , i = 1,…, k; fj(x) £ Cj , j = 1,…, n, При этом функции fj(x) могут зависеть как одновременно от всех переменных, так и от некоторой их части. Ограничения типа неравенств характеризуют или физические ограничения на процессы в изучаемом объекте (например, ограничения температуры), или технические ограничения, связанные с условиями работы объекта (например, предельная скорость резания).
Возможности исследования моделей существенно зависят от свойств (рельефа) поверхности отклика, в частности, от количества имеющихся на ней «вершин» и ее контрастности. Количество вершин (впадин) определяет модальность поверхности отклика. Если в области определения на поверхности отклика имеется одна вершина (впадина), модель называется унимодальной. Характер изменения функции при этом может быть различным (Рис. 1.5).
| W |  | W | W |
| x* x | x* x | x* x |
а б в Рис. 1.5 Модель может иметь разрывы первого рода (см. рис. 1.5. а). Непрерывная унимодальная модель может иметь точки разрыва производной – разрывы второго рода (см. рис. 1.5. б). На рис.
1.5 в показана непрерывно-дифференцируемая унимодальная модель. Для всех трех случаев, представленных на рис. 1.5, выполняется общее требование унимодальности: Если W(x*) = extr W, то из условия х1 x2 x* (x1 > x2 > x*) следует
W(x1) W(x2) W(x*) , если extr – максимум, или W(x1) > W(x2) > W(x*) , если extr – минимум, то есть, по мере удаления от экстремальной точки значение функции W(x) непрерывно падает (растет). Наряду с унимодальными бывают полимодальные модели (Рис. 1.6).
 |
| W | x2 | X1* В лекции «3 Логические функции» также много полезной информации. X2* |
| x1* x2* x3* x | x1 |

Рис. 1.6 Другим важным свойством поверхности отклика является ее контрастность, показывающая чувствительность результирующей функции к изменению факторов. Контрастность характеризуется величинами производных. Продемонстрируем характеристики контрастности на примере двумерной поверхности отклика (Рис. 1.7).
Точка а расположена на «склоне», характеризующем равную контрастность по всем переменным хi (i=1,2); точка b расположена в «овраге», в котором различная контрастность по различным переменным (имеем плохую обусловленность функции); точка с расположена на «плато», на котором низкая контрастность по всем переменным хi говорит о близости экстремума.
Источник: studizba.com
Математическое моделирование бизнес-процессов расчета арендных платежей в отделе управления имуществом
Ключевой проблемой в плане сдачи в аренду площадей в ЗАО «Тандер» является то, что это непрофильная деятельность. Как следствие, в штатном расписании соответствующие должности (брокер), четко не прописаны. Данная задача вменена сотрудникам отдела управления имуществом. И брокером назначается один из сотрудников сектора учета – ведущий инженер.
Назначенный брокером работник, полностью от своих обязанностей не освобождается, ему лишь выделяется ресурс времени в 1 час в день на выполнение работ по начислению арендной платы и пени. Соответственно, время на процессы работы с арендаторами должно быть минимальным.
Мною составлена математическая модель для оценки времени, требуемого в текущих условиях для начисления арендной платы и пени по договорам аренды. 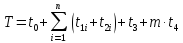 Где:
Где: 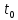 –время формирования списка всех активных договоров аренды;
–время формирования списка всех активных договоров аренды; 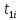 –время расчета платы для i-го арендатора;
–время расчета платы для i-го арендатора;  –время установления факта оплаты за текущий месяц i-м арендатором по его договору аренды;
–время установления факта оплаты за текущий месяц i-м арендатором по его договору аренды; 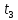 –время определения всех арендаторов, просрочивших оплату в текущем месяце;
–время определения всех арендаторов, просрочивших оплату в текущем месяце; 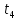 –среднее время на начисление пени; n – количество активных арендаторов; m – количество арендаторов, просрочивших оплату в текущем месяце.
–среднее время на начисление пени; n – количество активных арендаторов; m – количество арендаторов, просрочивших оплату в текущем месяце.
Следующим шагом применения математической модели было ее применение для получения количественной оценки затрат времени. Для этих целей каждый из параметров был измерен опытным путем и было получено следующее: Время формирования списка всех активных договоров аренды; 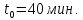 Среднее время расчета платы для i-го арендатора;
Среднее время расчета платы для i-го арендатора; 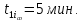 Среднее время установления факта оплаты за текущий месяц i-м арендатором по его договору аренды;
Среднее время установления факта оплаты за текущий месяц i-м арендатором по его договору аренды; 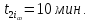 Среднее время определения всех арендаторов, просрочивших оплату в текущем месяце;
Среднее время определения всех арендаторов, просрочивших оплату в текущем месяце; 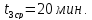 Среднее время на начисление пени;
Среднее время на начисление пени; 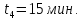 Среднее количество активных арендаторов; n = 50 Среднее количество арендаторов, просрочивших оплату в месяце; m = 20 Данные показатели были подставлены в формулу
Среднее количество активных арендаторов; n = 50 Среднее количество арендаторов, просрочивших оплату в месяце; m = 20 Данные показатели были подставлены в формулу 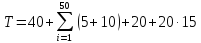
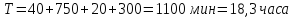 Если учесть, что в рабочем месяце 21 день, а на обработку договоров аренды отводится 1 час в день, то легко заметить, что ведущий инженер сотрудник отдела управления имуществом, являющийся «Брокером» заканчивает процесс начисления арендной платы и пени ровно к началу следующего месяца. Разумеется, такие задержки неприемлемы.
Если учесть, что в рабочем месяце 21 день, а на обработку договоров аренды отводится 1 час в день, то легко заметить, что ведущий инженер сотрудник отдела управления имуществом, являющийся «Брокером» заканчивает процесс начисления арендной платы и пени ровно к началу следующего месяца. Разумеется, такие задержки неприемлемы.
Постановка задачи выпускной квалификационной работы
Моделирование и оптимизация бизнес-процессов отдела управления имуществом зао «Тандер»
Нахождение оптимальных параметров математической модели
- Текущая форма: бумажные договоры, сортировка по дате;
- Форма 1: бумажные договоры, сортировка по алфавиту;
- Форма 2: электронные договоры в виде отдельных документов, организация каталога файлов.
- Форма 3: база данных и соответствующая информационная система.
Источник: studfile.net
Экономико-математическое моделирование в управлении производством
При разработке систем управления производственными процессами консультанты используют целый спектр различных методик. В данной статье будет отражена лишь одна из них, но очень существенная – экономико-математическое моделирование. Редкий проект без него реализуем, а как правильнее применять ЭММ, какие инструменты привлекать в тех или иных ситуациях, рассказывает Антонян Левон.
Л.В.АНТОНЯН — руководитель центра компетенций по экономико-математическим методам консалтинговой компании «А ДАН ДЗО», кандидат физико-математических наук.
Цели и задачи ЭММ
Применение математических методов в моделировании, анализе, прогнозировании и оптимизации производственных, управленческих, транспортно-логистических, торгово-распределительных и других экономических процессов – а именно так можно определить экономико-математическое моделирование (ЭММ) – имеет давнюю историю. Во всяком случае, в отношении элементарных экономических расчетов это можно утверждать наверняка.
А серьезные математические методы пришли в экономику примерно в 60-х годах прошлого (20-го) века – когда экономика усложнилась до такой степени, что принятие эффективных управленческих решений на основе лишь опыта и интуиции стало практически невозможным. Хотя, разумеется, сами эти методы появились существенно раньше: так, например, методы исследования операций, ныне активно используемые в управлении бизнес-процессами, широко применялись еще в ходе второй мировой войны при планировании боевых действий.
А современный бизнес – это тоже своего рода война, и успех в нем в значительной мере зависит именно от оперативности и качества принимаемых управленческих решений. Отсюда – востребованность консультационных услуг по оптимизации управления бизнес-процессами. Отсюда и востребованность математических методов в работе консультантов, которые позволяют разрабатывать эффективные инструменты поддержки принятия управленческих решений, повышать точность, оперативность и глубину экономических расчетов, одновременно снижая их трудоемкость. А многие задачи, возникающие в современной экономике, вообще не решаемы без применения адекватного математического аппарата.
Следует отметить и дополнительный (попутный) эффект внедрения ЭММ в управление бизнес процессами. Поскольку ЭММ так или иначе имеет дело с информацией — анализирует и перерабатывает ее (порождая новую информацию), — то применение ЭММ ведет к упорядочиванию информационно-аналитического обеспечения процессов управления: формулируются и проводятся в жизнь определенные требования к составу информации, способам ее хранения и анализа.
Естественно, в компании, работающей на рынке услуг делового консультирования, разработка экономико-математических моделей не может быть самоцелью.
Однако можно с уверенностью утверждать, что большинству консультантов так или иначе приходится в ходе своей работы заниматься построением разного рода моделей – прежде всего, с использованием популярного и достаточно хорошо всем знакомого инструмента «Microsoft Excel». В силу вполне объективных причин это нередко приводит к распылению и дублированию усилий, а разрабатываемые модели оказываются ориентированными на частные, локальные задачи. Наличие в компании центра компетенций по математическим методам – пусть и в лице всего одного человека – позволяет избегать этих недостатков, повышать качество разрабатываемых моделей до уровня тиражируемых (а в каких-то случаях – и коммерческих) продуктов, допускающих, как минимум, их многократное применение в проектах компании. При этом консультанты не освобождаются от необходимости разрабатывать свои собственные модели, но они получают в свое распоряжение набор специализированных модулей, которые легко встраиваются в разрабатываемые модели и позволяют решать разнообразные типовые задачи.
Разумеется, разработкой средств автоматизации работы консультантов дело отнюдь не ограничивается.
Простейшая схема применения экономико-математического моделирования во внешних консалниговых проектах компании может предусматривать выполнение расчетов, необходимых для экономического обоснования разрабатываемых проектных решений и передачу заказчикам только лишь результатов этих расчетов. При этом использованные в расчетах модели и инструменты заказчику не предоставляются, хотя в материалы проектов обычно включаются более или менее подробные описания использованных методик и алгоритмов.
Другой вариант может предусматривать передачу разрабатываемых моделей и инструментов в самостоятельное пользование заказчикам, причем как в рамках отдельных проектов по разработке подобных инструментов, так и, возможно, в рамках более широких проектов по оптимизации бизнес-процессов.
Наконец, может предполагаться внедрение разрабатываемых моделей и инструментов на предприятиях заказчиков, то есть их адаптация к условиям заказчика, обучение персонала, пробная эксплуатация, возможная интеграция с корпоративными информационными системами и другими имеющимися у заказчиков программными продуктами.
Инструментарий ЭММ
Использование именно Excel’а в качестве средства разработки экономико-математических моделей оправдывается не только высокой скоростью моделирования в среде Excel. Модели, разрабатываемые на базе этого поистине «народного» инструмента, как правило, наиболее просты в освоении, и даже их самостоятельная адаптация к меняющимся условиям может быть для более или менее квалифицированных пользователей Excel’а вполне посильной задачей. К тому же, на местах (например, в цехах предприятий) использование иных программных средств может оказаться затруднительным – хотя бы в силу ресурсных ограничений (это могут быть и устаревшие компьютеры, и отсутствие локальной сети, и низкая квалификация пользователей).
Конечно, для работы с большими массивами данных Excel приспособлен, плохо, поэтому для хранения данных мы при необходимости используем специализированные инструменты управления базами данных (такие, как Microsoft Access или Microsoft SQL Server), а у заказчика роль источника информации может играть, в частности, база данных его корпоративной информационной системы.
В каких-то случаях вычислительные процедуры, реализованные в среде Excel, не обеспечивают необходимого быстродействия – и тогда мы реализуем их другими средствами (например, на языке программирования FORTRAN), причем помещаем их в отдельные динамически загружаемые библиотеки (DLL), откуда – вот что здесь чрезвычайно важно! – они могут быть вызваны не только из Excel’а, но и, к примеру, из той же корпоративной информационной системы заказчика. А что же в этой ситуации остается от Excel’а? Фактически – только интерфейс пользователя, при разработке которого вся мощь Excel’а (обширный набор встроенных функций, красивые графики, богатые возможности форматирования таблиц. ) оказывается в нашем распоряжении. А в дальнейшем и интерфейс пользователя можно при желании перенести на платформу заказчика.
Таким образом, что же получается? Мы, если угодно, делаем «прототип» требуемого заказчику программного модуля (полнофункциональный, работающий прототип!), причем делаем достаточно быстро (ведь это Excel!), затем этот прототип обкатывается (с участием заказчика), после чего можно переносить его на нужную платформу (интересно, что на практике этого зачастую не делается, поскольку разработанный в Excel’е прототип может заказчика вполне удовлетворять).
Особо подчеркнем: мы не занимаемся разработкой программных продуктов класса комплексных систем автоматизации управления предприятием, т.е. корпоративных информационных систем (КИС) и других систем подобного масштаба. В то время как эти системы обычно предназначены для автоматизации стандартных (в первую очередь, учетных) функций (таких, как бухгалтерский учет, управление складом, планирование производства и т.д.), мы ориентируемся на решение специфических, нестандартных задач (требующих именно применения ЭММ), которые в функциональность КИС могут вообще не входить.
Классификация ЭММ
В нижеследующей таблице приведены основные типы экономико-математических моделей.
Тип моделей
Предназначение, цель применения
Экономические расчеты, основанные на принципе баланса наличия, поступления/производства и выбытия/расходования различных видов ресурсов: материальных, энергетических, машинных, денежных и др.
Прогнозирование развития моделируемой экономической системы на основе трендов (длительных тенденций изменения) ее основных показателей
Выбор наилучшего из имеющихся вариантов производства, распределения или потребления продукции, размещения объектов инфраструктуры, маршрутов движения и т.д.
Изучение взаимосвязей производственно-экономических показателей моделируемой системы в условиях влияния случайных факторов: корреляционно-регрессионный анализ, факторный анализ, анализ чувствительности и т.д.
Имитация (как правило, на ЭВМ) процесса функционирования изучаемого объекта во времени
Не случайно классификация ЭММ открывается балансовыми моделями. Потому что без балансовых расчетов не обходится практически ни одна мало-мальски содержательная экономико-математическая модель: ведь, к примеру, любой расчет потребностей в материалах, рабочей силе, производственных мощностях, денежных средствах основывается именно на принципе баланса. Можно здесь упомянуть и метод межотраслевого баланса, известный также как метод «затраты-выпуск» и основанный на принципе баланса производства и потребления продукции отраслей народного хозяйства целой страны.
В общем случае балансовые расчеты сводятся к решению системы уравнений (чаще всего линейных).
Важным преимуществом балансовых расчетов является их относительная простота (по крайней мере, в тех случаях, когда размерность задачи не слишком высока).
Однако для получения надежных, качественных результатов одних балансовых расчетов обычно бывает недостаточно – по крайней мере, по трем причинам.
Во-первых, любой расчет (не только балансовый) всегда базируется на определенных исходных предположениях, достоверность которых обычно бывает под вопросом. Эти предположения могут касаться, например, будущей динамики валютного курса, темпа инфляции, объема и цены реализации продукции.
В таких, как говорят, «условиях неопределенности» одного (базового) расчета совершенно недостаточно, потому что необходимо понимать, что будет, если те или иные входные параметры отклонятся от исходных (базовых) значений. Для этого в модели расчета можно предусмотреть несколько сценариев – например, базовый, оптимистический и пессимистический – и проанализировать результаты расчетов во всех предусмотренных случаях. Такой путь, конечно, предпочтительнее безальтернативного варианта, но он, с одной стороны, ведет к усложнению исходной модели, а, с другой, — всё равно не дает полной картины: в частности, не позволяет количественно оценить риски, обусловленные неопределенностью. Другой вариант состоит в (случайном, вообще говоря) варьировании входных переменных (параметров) анализируемой модели с целью исследования степени и характера влияния этих вариаций на выходные переменные (результаты расчетов). Этот так называемый анализ чувствительности – и здесь мы переходим к классу статистических моделей – позволяет:
- Проверить корректность построенной модели;
- Оценить ее практическую применимость;
- Выявить входные параметры, наиболее существенно влияющие на поведение результирующих переменных;
- Оценить риски и сопряженные с ними размеры потерь в условиях неопределенности.
Во-вторых (возвращаемся к недостаткам чисто балансовых моделей), во многих случаях балансовые расчеты дают грубые, недостоверные результаты. Например, расчет потребностей в персонале на основе фонда рабочего времени работников и норм времени выполнения операций никак не учитывает возможные простои персонала вследствие временного отсутствия тех или иных ресурсов и поэтому дает, вообще говоря, заниженные оценки необходимой численности работников. Более точные оценки в подобных ситуациях может дать имитационное моделирование, которое воспроизводит функционирование анализируемой системы во времени обычно путем имитации элементарных событий (например, начала или завершения выполнения технологических операций), меняющих состояние системы, с сохранением логической взаимосвязи и последовательности этих событий. Имитационная модель обычно «проигрывается» многократно, что позволяет перебирать различные возможные комбинации значений входных параметров и получать статистически надежные прогнозы поведения моделируемой системы и оценки таких характеристик ее функционирования, как производительность, время обслуживания заказов, коэффициенты загрузки и простоя оборудования, длины очередей и т.д.
В-третьих, чисто балансовые расчеты вообще непригодны, например, в ситуации выбора наилучшего из имеющихся вариантов, т.е. для решения оптимизационных задач.
Опыт применения ЭММ
Автор имеет обширный опыт экономико-математического моделирования (в первую очередь, но не только в среде MS Excel). Разработанный им модуль анализа чувствительности для MS Excel легко подключается к любой Excel’овской модели, позволяя варьировать входные переменные модели по задаваемой пользователем схеме и анализировать влияние этих вариаций на выходные переменные модели. При этом варьирование входных переменных может моделироваться как по заданным случайным законам распределения (метод Монте-Карло), так и с использование заданных детерминированных последовательностей (в частности, многомерных решеток) значений.
Также в среде Excel, но с подключением отдельно написанных (на FORTRAN’е) процедур моделирования автором была разработана Система планирования движения ресурсов, предназначенная для балансового и имитационного моделирования бизнес-процессов. С помощью этого инструмента были построены (для нужд коммерческих проектов компании) имитационные модели работы центрального распределительного склада крупной компании, а также функционирования крупной железнодорожной станции. В первом случае склад проектировался «с нуля», и модель потребовалась для обоснования необходимой численности ресурсов этого склада: сооружений, складской техники и персонала. Во втором случае изучались перспективы развития перегрузочной деятельности на железнодорожном переходе (с узкой колеи на широкую), и в задачи моделирования входило обоснование необходимой численности ресурсов перегрузочных мест (механизмов и производственного персонала) и станции (путей и маневровых локомотивов), расчет загрузки сооружений, техники и персонала, выявление узких мест и путей их устранения для различных сценариев развития станции.
Еще одним примером может служить разработанные автором инструменты автоматизации управления централизованной доставкой (ЦД) материально-технических ресурсов для нужд крупной территориально распределенной компании. Этот инструментарий (также разработанный на платформе MS Excel) обеспечивает автоматизацию таких функций, как планирование и контроль выполнения перевозок, генерация сопроводительных документов (планов отгрузки и доставки, заявок на транспорт и т.д.), а также тарификация услуг ЦД на основе статистических данных по перевозкам за предшествующие периоды (особенность тарификации ЦД состоит в том, что тарифицируется не время или расстояние, а маршруты перевозок).
Автору доводилось также решать разнообразные оптимизационные задачи. В качестве примера можно привести задачу оптимизации товаропроводящих сетей (в частности, территориально-распределенного складского хозяйства), решавшуюся методами целочисленного линейного программирования. Этими же методами решалась задача оптимизации вахтовых перевозок (минимизации затрат на аренду транспорта) на крупном нефтегазодобывающем предприятии. Еще один пример – задача оптимизации кольцевых (замкнутых) маршрутов (так называемая «задача коммивояжера»), решавшаяся методом (имитации) динамического отжига.
Из примеров иного рода можно, в частности, упомянуть модель тарификации рабочих мест и формирования должностных окладов, а также программу тестирования персонала.
Источник: up-pro.ru
