Аннотация научной статьи по экономике и бизнесу, автор научной работы — Смирнов Вячеслав Дмитриевич, Колокольчиков Александр Владимирович
Цель статьи изучить примеры использования теории игр в жизни и бизнесе . Для достижения поставленной цели были решены следующие задачи: изучен имеющийся материал по данной тематике; рассмотрены понятие теории игры и классификация ее моделей; изучены примеры использования математической теории игры в жизни и бизнесе . Для решения поставленных задач в статье использованы такие методы, как анализ, синтез, описание и обобщение. Результат исследования следующий: было показано, что в настоящее время теория игр достаточно широко применяется во многих сферах жизни человечества и позволяет решить достаточно широкий круг задач.
i Надоели баннеры? Вы всегда можете отключить рекламу.
Похожие темы научных работ по экономике и бизнесу , автор научной работы — Смирнов Вячеслав Дмитриевич, Колокольчиков Александр Владимирович
Модели теории игр в экономике и бизнесе
Некоторые аспекты применения теории игр в экономике
Справедливая стоимость фирм при экономической интеграции
Теоретико-игровое моделирование взаимодействия субъектов в инновационной сфере
Использование теории игр в управлении цепочкой поставок
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
i Надоели баннеры? Вы всегда можете отключить рекламу.
GAME THEORY IN LIFE AND BUSINESS
The purpose of the article is to study examples of the use of mathematical game theory in life and business . To achieve this goal, the following tasks were solved: the available material on this topic was studied; the concept of game theory and the classification of its models were considered; examples of the use of mathematical game theory in life and business were studied. To solve these problems, the article uses such methods as analysis, synthesis, description and generalization. The result of the study is as follows: it was shown that game theory is currently widely used in many areas of human life and allows you to solve a wide range of problems.
Текст научной работы на тему «Теория игр в жизни и бизнесе»
ТЕОРИЯ ИГР В ЖИЗНИ И БИЗНЕСЕ 1 2 Смирнов В.Д. , Колокольчиков А.В.
1Смирнов Вячеслав Дмитриевич — студент, кафедра менеджмента;
2Колокольчиков Александр Владимирович — кандидат физико-математических наук, доцент,
кафедра математики, Иркутский национальный исследовательский технический университет,
Аннотация: цель статьи — изучить примеры использования теории игр в жизни и бизнесе. Для достижения поставленной цели были решены следующие задачи: изучен имеющийся материал по данной тематике; рассмотрены понятие теории игры и классификация ее моделей; изучены примеры использования математической теории игры в жизни и бизнесе. Для решения поставленных задач в статье использованы такие методы, как анализ, синтез, описание и обобщение. Результат исследования следующий: было показано, что в настоящее время теория игр достаточно широко применяется во многих сферах жизни человечества и позволяет решить достаточно широкий круг задач.
Ключевые слова: математика, теория игр, социум, бизнес.
GAME THEORY IN LIFE AND BUSINESS 12 Smirnov V.D. , Kolokolchikov A.V.
1Smirnov Vyacheslav Dmitrievich — Student, DEPARTMENT OF MANAGEMENT;
2Kolokolchikov Alexander Vladimirovich — Candidate of Physical and Mathematical Sciences,
Associate Professor, DEPARTMENT OF MATHEMATICS, IRKUTSK NATIONAL RESEARCH TECHNICAL UNIVERSITY, IRKUTSK
Abstract: the purpose of the article is to study examples of the use of mathematical game theory in life and business. To achieve this goal, the following tasks were solved: the available material on this topic was studied; the concept of game theory and the classification of its models were considered; examples of the use of mathematical game theory in life and business were studied. To solve these problems, the article uses such methods as analysis, synthesis, description and generalization. The result of the study is as follows: it was shown that game theory is currently widely used in many areas of human life and allows you to solve a wide range of problems. Keywords: math, game theory, society, business.
Для анализа решений в различных сферах широко используются математические модели. В качестве математических методов при отыскании оптимальных решений используют методы теории игр.
Теория игр изучает конфликты двух или более сторон, именуемых играми. Под изучение попадают сами игры, стратегии, применяемые в играх, а также модели поведения в играх. Поведение игроков обусловлено стратегиями. Стратегии, присущие игрокам носят название «модели поведения».
В связи с вышесказанным можно с уверенностью сказать о том, что изучение применения математической теории игр в жизни и бизнесе является весьма актуальным.
Основные понятия теории игр и классификация моделей
Теория игр — совокупность математических методов решения конфликтных ситуаций (столкновений интересов) [1]. В теории игр игрой называется математическая модель конфликтной ситуации. Предмет особого интереса теории игр — исследование стратегий принятия решений участников игры в условиях неопределённости. Неопределённость связана с тем, что две или более стороны преследуют противоположные цели, а результаты любого действия каждой из сторон зависят от ходов партнёра. При этом каждая из сторон стремится принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени.
Исход игры — выигрыш, проигрыш либо ничья, так же полученное вознаграждение. Стратегия — умозаключения, из которых исходит выбор действий в игре. Равновесие Нэша — так называется набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники свои стратегии не меняют. Часто в играх с равновесием, изменение стратегии всех участников приведёт к увеличению выигрыша, но каждому отдельно взятому участнику игры невыгодно менять стратегию.
Модель поведения — присущая игроку стратегия либо стратегии. В теории игр принято существует достаточно много различных классификаций моделей, однако чаще всего выделяют следующую классификацию моделей:
— игры с не противоположными интересами [2].
Использование математической теории игр в жизни и бизнесе
Теория игр применяется в социологии с целью понять, объяснить и контролировать игры с социальной составляющей. В свою очередь в психологии теория игр изучает действия каждого отдельного обособленного игрока. В той или иной форме теорию игр используют психологи, социологи, политики, маркетологи и многие другие люди. Социологи пытаются понять причины действий групп игроков и использовать полученные знания. Они моделируют игры, проводят исследования, чтобы найти наиболее выгодную стратегию.
В политике теория игр применяется для анализа ситуаций и взаимодействий игроков (как правило стран), для решения игр и для поиска наилучших стратегий. У стран есть ряд конфликтов: территории, торговля, альянсы. Теория игр помогает достичь компромисса. Так же теория игр применяется в голосованиях — кандидаты прибегают к разным стратегиям для увеличения шансов выигрыша.
В экономике теория игр применяется повсеместно. Возможно, вы встречали игру «Неблагоприятная монополия», это очень хороший пример игры. Экономические игры -аукционы, модели монополии и олигополии, рынки и многое другое. В экономике существуют модели, которые характеризуют те или иные игры и являются универсальными — и могут быть применены во всех играх, подходящих по характеристике.
Таким образом, теория игр полезна для принятия важных решений, логического мышления, умения мыслить на шаг вперёд, а также расширения кругозора.
Практическое применение в управлении компаниями
Теория игр довольно широко используется в управлении предприятиями, например с ее помощью можно решать вопросы, касающиеся создание совместных предприятий, вступление на новые рынки и даже проведения принципиальной ценовой политики.
Возникает вопрос, какую же пользу могут извлечь предприятия из анализа на базе теории игр? Рассмотрим известный пример столкновения интересов гиганта IT индустрии IBM и компании Telex.
В начале 80-х годов прошлого века компания IBM являлась крупнейшим игроком на рынке персональных компьютеров, а компания Telex принимала решение по вопросу о выходе на рынок персональных компьютеров с переналадкой своего производства. В данной ситуации компания аутсайдеру нужно принять решении о выходе или не выходе на рынок.
В свою очередь компания гигант может отреагировать на появление нового игрока агрессивно либо дружественно. Две компании в этот момент вступают в двухэтапную игру, в которой первый ход делает более слабая компания. Данную ситуацию можно представить в виде дерева решений.
Будет рассматриваться два состояния — выход на рынок и последовавшая дружественная реакция со стороны IBM; выход на рынок и агрессия со стороны IBM. Второе же равновесие будет считаться не состоятельным.
Из развернутой формы мы делаем вывод о том, что для уже закрепившейся на рынке компании нерационально реагировать агрессивно на появление конкурента, ведь при агрессивном поведении компания IBM получает один поток платежей, при дружественном три. Компания Telex к тому же знает, что для монополиста не рационально начинать действия по ее вытеснению, поэтому она принимает решение о вступлении на рынок. Грозившие потери в этом случае компания Telex не понесет [4]. В данной ситуации компания Telex могла бы выбрать ход «не выход на рынок», если бы предварительный анализ дал убедительный ответ, что выход на рынок вызовет агрессивную реакцию со стороны большой компании IBM. В данной ситуации рационально было бы выбрать ход «не выход на рынок» при вероятности агрессивного ответа 0,5, в соответствии с критерием ожидаемой стоимости.
Как мы увидели на примере знания в сфере теории игр можно использовать в практике предприятий, чтобы позволить двум компаниям получить ситуацию выигрыш/выигрыш.
Сегодня консультанты с подготовкой в области игр быстро и однозначно выявляют возможности, которыми предприятия могут воспользоваться для заключения стабильных и долгосрочных договоров с клиентами, партнерами по разработкам и т.д. [3]. Заключение
Таким образом, в ходе проведения данной работы было показано, что в настоящее время теория игр достаточно широко применяется во многих сферах жизни человечества и позволяет решить достаточно широкий круг задач наиболее последовательно теория игр применяется в экономике, где конфликтные ситуации возникают, например, в отношениях между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Применение теории игр можно найти и в политике, социологии, биологии, военном искусстве.
Список литературы /References
1. Математическая теория игр. Примеры записи и решения игр из жизни. [Электронный ресурс]. Свободный доступ: https://function-x.ru/games_theory_examples.html (дата обращения: 17.05.2020).
2. Ганичева А.В., Ганичев А.В. Модели теории игр в экономике и бизнесе [Текст] / А.В. Ганичева, А.В. Ганичев // Эпохи науки, 2019. № 20. С. 581-584.
Источник: cyberleninka.ru
Некоторые примеры теории игр в экономике
В качестве примеров применения теории игр в экономике можно назвать решения по поводу проведения принципиальной ценовой политики, вступления на новые рынки, кооперации и создания совместных предприятий, определения лидеров и исполнителей в области инноваций, вертикальной интеграции и т.д.
Рассмотрим двух гигантов, конкурирующих на рынке производства пассажирских самолетов: «Боинг» и «Эйрбас». Предельные издержки производства самолетов одинаковы у каждой компании и равны 10 млн. долларов за штуку.
Рыночный спрос на самолёты показан в таблице 1.
Таблица 1 – Рыночный спрос на самолёты
| P, млн. долл. | Q, штук |
В таблице 2 приведена прибыль конкурентов, если они договорятся о разделе рынка пополам.
Таблица 2 – Прибыль компаний «Боинг» и «Эйрбас» в случае раздела рынка
| P, млн. долл. | Q, штук | TR, млн. долл. | TC, млн. долл. | Общая прибыль | Прибыль каждого участника |
| -2000 | -1000 |
Продолжение таблицы 2
Прибыль участников будет максимальна, если они оба произведут по 45 самолетов (вместе 90) и равна в этом случае 2025 млн. долл. Эта точка является Парето-оптимумом, то есть в ней состояние одного участника нельзя улучшить без ухудшения состояния другого.
Каждый из участников может думать следующим образом:
Если я произвожу 45 самолетов и мой конкурент производит 45 самолетов, то наша общая прибыль будет максимальной, и я получу половину от максимальной общей прибыли. Однако что мешает мне произвести не 45, а 55 самолетов? В этом случае, если мой конкурент не предпримет ответных действий, общий объем продаж вырастет до 100, цена упадет до 50, а получу выручку 55∙50=2750 и прибыль 2750-550=2200. Тогда прибыль моего конкурента составит 50∙45-10∙45=1800.
Точно также может думать и другой участник, и в таком случае они оба произведут по 55 самолетов. В этом случае общий объём продаж вырастет до 110, цена упадет до 45, общая прибыль будет равна 1925, и каждый из участников получит прибыль 1925.
Игра этой ситуации описывается следующей матрицей выигрышей рисунок 4.
| Боинг | |||
| Произвести 45 | Произвести 55 | ||
| Эйрбас | Произвести 45 | (2025;2025) | (2200;1800) |
| Произвести 55 | (1800;2200) | (1925;1925) |
Рисунок 4 – Матрица выигрышей для компаний «Боинг» и «Эйрбас»
Первое значение в скобках означает прибыль Боинга, второе – прибыль Эйрбаса.
Если между участниками не заключено договоренностей, то каждый из них имеет стимулы произвести 55, а не 45 штук, чтобы увеличить свою прибыль. В этом случае производство 55 штук является доминирующей стратегий для каждого участника. Нэш-равновесие устанавливается в ситуации, когда они оба производят по 55 штук и получают прибыль в размере 1925 млн. долл. Это равновесие не является Парето-оптимальным.
Данная ситуация показывает, как эгоистические интересы каждого из участников мешают им достигнуть оптимального значения прибыли.
Рассмотрим пример «доминирующей стратегии», в котором одним из участников принимается решение относительно проникновения на новый рынок. Возьмем предприятие, которое выступает в качестве монополиста на каком-либо рынке. Другое предприятие обдумывает вопрос о проникновении на рынок. Компания-аутсайдер может принять решение о вступлении или невступлении на рынок.
Компания-монополист может отреагировать на появление нового конкурента агрессивно или дружественно. Оба предприятия вступают в двухэтапную игру, в которой первый ход делает компания-аутсайдер. Игровая ситуация с указанием платежей показана в виде дерева на рисунке 3.
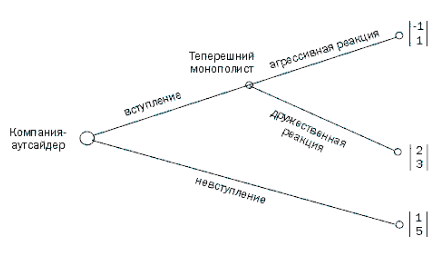
Рисунок 3 – Решение о проникновении на рынок
Та же самая игровая ситуация может быть представлена и в нормальной форме (рисунок 4). Здесь обозначены два состояния – «вступление – дружественная реакция» и «невступление – агрессивная реакция». Очевидно, что второе равновесие несостоятельно. Из развернутой формы следует, что для уже закрепившейся на рынке компании нецелесообразно реагировать агрессивно на появление нового конкурента: при агрессивном поведении теперешний монополист получает 1(платеж), а при дружественном – 3. Компания-аутсайдер к тому же знает, что для монополиста не рационально начинать действия по ее вытеснению, и поэтому она принимает решение о вступлении на рынок. Грозившие потери в размере (-1) компания-аутсайдер не понесет.
Рисунок 4 – Нормальная форма игры, предметом которой является проникновение на рынок
Первое значение в скобках означает прибыль компании-монополиста, второе – прибыль компании-аутсайдера.
Подобное рациональное равновесие характерно для «частично усовершенствованной» игры, которая заведомо исключает абсурдные ходы. Такие равновесные состояния на практике в принципе довольно просто найти. Равновесные конфигурации могут быть выявлены с помощью специального алгоритма из области исследования операций для любой конечной игры. Игрок, принимающий решение, поступает следующим образом: вначале делается выбор «лучшего» хода на последнем этапе игры, затем выбирается «лучший» ход на предшествующем этапе с учетом выбора на последнем этапе и так далее, до тех пор пока не будет достигнут начальный узел дерева игры.
Компаниям полезно в эксплицитном виде обдумывать возможные реакции партнеров по игре. Изолированные хозяйственные расчеты, даже опирающиеся на теорию принятия решений, часто носят, как в изложенной ситуации, ограниченный характер. Так, компания-аутсайдер могла бы и выбрать ход «невступление», если бы предварительный анализ убедил ее в том, что проникновение на рынок вызовет агрессивную реакцию монополиста. В этом случае в соответствии с критерием ожидаемой стоимости разумно выбрать ход «невступление» при вероятности агрессивного ответа 0,5.
Эти знания можно использовать в практике предприятий, чтобы помочь двум фирмам достичь ситуации «выигрыш – выигрыш». Сегодня консультанты с подготовкой в области игр быстро и однозначно выявляют возможности, которыми предприятия могут воспользоваться для заключения стабильных и долгосрочных договоров с клиентами, субпоставщиками, партнерами по разработкам и т.п.
Практическая часть
Швейное предприятие реализуется свою продукцию через магазин. Сбыт зависит от состояния погоды. В условиях теплой погоды предприятие реализует a костюмов и b платьев, а при прохладной погоде — c костюмов и d платьев. Затраты на изготовление одного костюма равны α0, а платья – β0 рублям, цена реализации соответственно равна α1 рублей и β1 рублей. Определить оптимальную стратегию предприятия.
a=1000, b=2300, c=1400, d=700,
Составим математическую модель задачи. В связи с возможными состояниями спроса фирма располагает двумя стратегиями.
1. F1 = (1000, 2300) – произвести 1000 костюмов и 2300 платьев,
2. F2 = (1400, 700) – произвести 1400 костюмов и 700 платьев.
Природа (рынок) располагает также двумя стратегиями:
1. D1 = погода теплая,
2. D2 = погода прохладная.
Если фирма примет стратегию F1 и спрос действительно будет находиться в первом состоянии, то есть погода будет теплой (D1), то выпущенная продукция будет полностью реализована и доход составит w11 =1000∙(40-20) + 2300∙(12-5) = 36100.
Если фирма примет стратегию F1, а спрос будет находиться в состоянии D2 (погода прохладная), то платья будут реализованы лишь частично, и доход составит: w12 = 1000∙(40-20) + 700∙(12-5) – (2300-700)∙5= 16900.
Аналогично, если фирма выберет стратегию F2, а природа – стратегию D1 (погода теплая), то доход составит (будут недораспроданы костюмы):
w21 =1000∙(40-20) + 700∙(12-5) – (1400-1000)∙20= 16900, а если природа выберет стратегию D2, то
w22 = 1400∙(40-20) + 700∙(12-5) = 32900.
Рассматривая фирму и природу в качестве двух игроков, получим платежную матрицу игры

,
которая будет служить игровой моделью задачи.
Поскольку максиминная стратегия игры составляет a = max (16900, 16900) = =16900, а минимаксная b = min (36100, 3290) = 32900, то цена игры лежит в диапазоне
Решим данную игру аналитическим методом. Средний выигрыш первого игрока, если он использует оптимальную смешанную стратегию xʹ=(x1ʹ,x2ʹ), а второй игрок – чистую стратегию, соответствующую первому столбцу платежной матрицы, равен цене игры ν:
Тот же средний выигрыш получает первый игрок, если второй игрок применяет стратегию, соответствующую второму столбцу платежной матрицы, то есть
Учитывая, что x1ʹ+x2ʹ=1, получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры:

Решаем эту систему и находим:
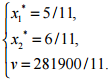
Оптимальная стратегия фирмы:

Таким образом, фирме оптимально произвести 1218 костюмов и 1427 платьев.
Количество возможных стратегий Получателя — 5, Плательщика — 4. Величины платежа образуют таблицу.
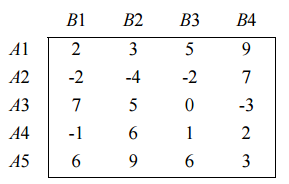
Требуется найти наиболее выгодную чистую стратегию первого игрока, выбирающего строку (Получателя).
1. В каждой строке найдем минимальное значение

2. Из полученных значений возьмем максимальное, то есть вычислим максимин

Найденное значение реализуется при выборе последней (пятой) стратегии А5 Получателя.
Ответ: наиболее выгодной для Получателя (при однократной игре) является стратегия А5, так как при любом выборе Плательщиком его стратегии величина платежа составит а = 3 или больше.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Интрилигатор, М. Математические методы оптимизации и экономическая теория: Учебное пособие/ М. Интрилигатор. – М.: Айрис — пресс, 2002. – 576 с.
2. Баканов, М.И. Теория экономического анализа: Учебное пособие/ М.И. Баканов, М.В. Мельник, А.Д. Шеремет. – 5-е изд., доп. и перераб. – М: Финансы и статистика, 2008. – 536 с.
3. Моргенштерн, О. Теория игр и экономическое поведение / О. Моргенштерн, Дж. фон Нейман. – М.: Книга по Требованию, 2012. – 708 с.
4. Замков, О.О. Математические методы в экономике: Учебное пособие/ О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных; под общ. ред.
А.В. Сидоровича. – 3-е изд., перераб. – М.: Издательство «Дело и Сервис», 2001. – 368 с.
5. Васин, А.А. Введение в теорию игр с приложениями к экономике: Учебное пособие/ А.А. Васин, В.В. Морозов. − М.: 2003. − 278 с.
6. Волков, И.К. Исследование операций: Учебник для вузов / И.К. Волков, Е.А. Загоруйко; под ред. B.C. Зарубина, А.П.
Крищенко. − М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 436 с.
7. Писарук, Н. Н. Введение в теорию игр: Учебное пособие / Н.Н. Писарук. − Минск: БГУ, 2015. – 256 c.
Источник: poisk-ru.ru
Что наша жизнь: 10 примеров того, зачем экономистам нужна теория игр
Игра — это любая ситуация, в которой прибыль агента зависит не только от его собственных действий, но и от поведения остальных участников. Если вы раскладываете дома пасьянс, с точки зрения экономиста и теории игр, это не игра. Она подразумевает обязательное наличие столкновения интересов.
В фильме «Игры разума» о Джоне Нэше, нобелевском лауреате по экономике, есть сцена с блондинкой в баре. В ней показана идея, за которую ученый и получил премию, — это идея равновесия по Нэшу, которое он сам называл управляющей динамикой.

По данным World RPS Society, камень является самым часто выбираемым ходом (37,8%). Бумагу ставят 32,6%, ножницы — 29,6%. Теперь вы знаете, что нужно выбирать бумагу. Однако, если вы играете с тем, кто тоже это знает, вам уже не надо выбирать бумагу, потому что от вас ожидается то же самое.
Есть знаменитый случай: в 2005 году два аукционных дома Sotheby“s и Christie”s решали, кому достанется очень крупный лот — коллекция Пикассо и Ван Гога со стартовой ценой в 20 миллионов долларов. Собственник предложил им сыграть в «Камень, ножницы, бумагу», и представители домов отправили ему свои варианты по электронной почте.
Sotheby“s, как они позже рассказали, особо не задумываясь, выбрали бумагу. Выиграл Christie”s. Принимая решение, они обратились к эксперту — 11-летней дочери одного из . Она сказала: «Камень кажется самым сильным, поэтому большинство людей его выбирают. Но если мы играем не с совсем глупым новичком, он камень не выбросит, будет ожидать, что это сделаем мы, и сам выбросит бумагу. Но мы будем думать на ход вперед, и выбросим ножницы».
Таким образом, вы можете думать на ход вперед, но это не обязательно приведет вас к победе, ведь вы можете не знать о компетенции вашего соперника. Поэтому иногда вместо чистых стратегий правильнее выбирать смешанные, то есть принимать решения случайно.
Так, в «Камне, ножницах, бумаге» равновесие, которое мы до этого не нашли, находится как раз в смешанных стратегиях: выбирать каждый из трех вариантов хода с вероятностью в одну третью. Если вы будете выбирать камень чаще, соперник скорректирует свой выбор. Зная это, вы скорректируете свой, и равновесия не выйдет. Но никто из вас не начнет менять поведение, если каждый просто будет выбирать камень, ножницы или бумагу с одинаковой вероятностью. Все потому что в смешанных стратегиях по предыдущим действиям невозможно предугадать ваш следующий ход.
Смешанные стратегии и спорт

Более серьезных примеров смешанных стратегий очень много. Например, куда подавать в теннисе или бить/принимать пенальти в футболе. Если вы ничего не знаете о вашем сопернике или просто постоянно играете против разных, лучшей стратегией будет поступать более-менее случайно.
Профессор Лондонской школы экономики Игнасио Паласиос-Уэрта в 2003 году опубликовал в American Economic Review работу, суть которой заключалась в поиске равновесия по Нэшу в смешанных стратегиях. Предметом исследования Паласиос-Уэрта выбрал футбол и в связи с этим просмотрел более 1400 ударов пенальти.
Разумеется, в спорте все устроено хитрее, чем в «Камне, ножницах, бумаге»: там учитывается сильная нога спортсмена, попадания в разные углы при ударе со всей силы и тому подобное. Равновесие по Нэшу здесь заключается в расчете вариантов, то есть, к примеру, определении углов ворот, в которые надо бить, чтобы выиграть с большей вероятностью, зная свои слабые и сильные стороны. Статистика по каждому футболисту и найденное в ней равновесие в смешанных стратегиях, показало, что футболисты поступают примерно так, как предсказывают экономисты. Вряд ли стоит утверждать, что люди, которые бьют пенальти, читали учебники по теории игр и занимались довольно непростой математикой. Скорее всего, есть разные способы научиться оптимально себя вести: можно быть гениальным футболистом, и чувствовать, что делать, а можно — экономистом, и искать равновесие в смешанных стратегиях.
В 2008 году профессор Игнасио Паласиос-Уэрта познакомился с Авраамом Грантом, тренером «Челси», который играл тогда в финале Лиги чемпионов в Москве. Ученый написал записку тренеру с рекомендациями по серии пенальти, которые касались поведения вратаря соперника — Эдвина ван дер Сара из «Манчестер Юнайтед».
Например, по статистике, он почти всегда отбивал удары на среднем уровне и чаще бросался в естественную для пробивающего пенальти сторону. Как мы определили выше, правильнее все-таки рандомизировать свое поведение с учетом знаний о сопернике. Когда счет по пенальти был уже 6:5, Николя Анелька, нападающий «Челси», должен был забивать. Показывая перед ударом в правый угол, ван дер Сар будто спросил у Анелька, не собирается ли он бить туда.
Суть в том, что все предыдущие удары «Челси» были нанесены именно в правый от пробивающего угол. Мы не знаем точно почему, может быть, из-за консультации экономиста бить в неестественную для них сторону, ведь по статистике к этому менее готов ван дер Сар. Большинство футболистов «Челси» были правшами: ударяя в неестественный для себя правый угол, все они, кроме Терри, забивали.
Видимо, стратегия была в том, чтобы Анелька пробил туда же. Но ван дер Сар, похоже, это понял. Он поступил гениально: показал в левый угол дескать «туда собрался бить?», от чего Анелька, наверное, пришел в ужас, ведь его разгадали. В последний момент он принял решение действовать по-другому, ударил в естественную для себя сторону, что и было нужно ван дер Сару, который взял этот удар и обеспечил «Манчестеру» победу. Эта ситуация учит случайному выбору, ведь в ином случае ваше решение может быть просчитано, и вы проиграете.
«Дилемма заключенного»

Pedro Ribeiro Simões
Наверное, самая известная игра, с которой начинаются университетские курсы о теории игр, — это «Дилемма заключенного». По легенде двух подозреваемых в серьезном преступлении поймали и заперли в разные камеры. Есть доказательство, что они хранили оружие, и это позволяет посадить их на небольшой срок. Однако доказательств, что они совершили это страшное преступление, нет.
Каждому по отдельности следователь рассказывает об условиях игры. Если оба преступника сознаются, оба же сядут на три года. Если сознается один, а подельник будет молчать, сознавшийся выйдет сразу, а второго посадят на пять лет. Если, наоборот, первый не сознается, а второй его сдаст, первый сядет на пять лет, а второй выйдет сразу. Если же не сознается никто, оба сядут на год за хранение оружия.
Равновесие по Нэшу здесь заключается в первой комбинации, когда оба подозреваемых не молчат и оба садятся на три года. Рассуждения каждого таковы: «если я буду говорить, я сяду на три года, если молчать — на пять лет. Если второй будет молчать, мне тоже лучше говорить: не сесть лучше, чем сесть на год».
Это доминирующая стратегия: говорить выгодно, независимо от того, что делает другой. Однако в ней есть проблема — наличие варианта получше, ведь сесть на три года хуже, чем сесть на год (если рассматривать историю только с точки зрения участников и не учитывать вопросы морали). Но сесть на год невозможно, ведь, как мы поняли выше, молчать обоим преступникам невыгодно.
Улучшение по Парето
Есть известная метафора про невидимую руку рынка, принадлежащая Адаму Смиту. Он говорил, что если мясник будет сам для себя стараться заработать деньги, от этого будет лучше всем: он сделает вкусное мясо, которое купит булочник на деньги от продажи булок, которые он, в свою очередь, тоже должен будет делать вкусными, чтобы они продавались. Но оказывается, эта невидимая рука не всегда работает, и таких ситуаций, когда каждый действует за себя, а всем плохо, очень много.
Поэтому иногда экономисты и специалисты по теории игр думают не об оптимальном поведении каждого игрока, то есть не о равновесии по Нэшу, а об исходе, при котором будет лучше всему обществу (в «Дилемме» общество состоит из двух преступников). С этой точки зрения, исход эффективен, когда в нем нет улучшения по Парето, то есть невозможно сделать кому-то лучше, не сделав при этом хуже другим.
Если люди просто меняются товарами и услугами, это Парето-улучшение: они делают это добровольно, и вряд ли кому-то от этого плохо. Но иногда, если просто дать людям взаимодействовать и даже не вмешиваться, то, к чему они придут, не будет оптимальным по Парето. Это и происходит в «Дилемме заключенного». В ней, если мы даем каждому действовать так, как им выгодно, оказывается, что всем от этого плохо. Всем было бы лучше, если бы каждый действовал не оптимально для себя, то есть молчал.
Трагедия общины

«Дилемма заключенного» — это игрушечная стилизованная история. Вряд ли вы ожидаете оказаться в подобной ситуации, но похожие эффекты есть везде вокруг нас. Рассмотрим «Дилемму» с большим количеством игроков, ее иногда называют трагедией общины. Например, на дорогах — пробки, и я решаю, как ехать на работу: на машине или на автобусе. Это же делают остальные.
Если я поеду на машине, и все решат сделать то же самое, будет пробка, но мы доедем с комфортом. Если я поеду на автобусе, пробка-то все равно будет, но ехать я буду некомфортно и не особо быстрее, поэтому такой исход еще хуже. Если же в среднем все ездят на автобусе, то я, сделав то же самое, довольно быстро доеду без пробки.
Но если при таких условиях поехать на машине, я тоже доеду быстро, но еще и с комфортом. Итак, наличие пробки не зависит от моих действий. Равновесие по Нэшу здесь — в ситуации, когда все выбирают ехать на машине. Что бы не делали остальные, мне лучше выбрать машину, потому что будет там пробка или нет, неизвестно, но я в любом случае доеду с комфортом.
Это доминирующая стратегия, поэтому в итоге все едут на машине, и мы имеем то, что имеем. Задача государства — сделать поездку на автобусе лучшим вариантом хотя бы для некоторых, поэтому появляются платные въезды в центр, парковки и так далее.
Другая классическая история — рациональное незнание избирателя. Представьте, что вы не знаете исход выборов заранее. Вы можете изучить программу всех кандидатов, послушать дебаты и после проголосовать за самого лучшего. Вторая стратегия — прийти на участок и проголосовать как попало или за того, кого чаще показывали по телевизору.
Какое поведение оптимально, если от моего голоса никогда не зависит, кто выиграет (а в 140-миллионной стране один голос никогда ничего не решит)? Конечно, я хочу, чтобы в стране был хороший президент, но я же знаю, что никто больше не будет изучать программы кандидатов внимательно. Поэтому не тратить на это время — доминирующая стратегия поведения.
Когда вас призывают прийти на субботник, ни от кого в отдельности не будет зависеть, станет двор чистым или нет: если я выйду один, я не смогу убрать все, или, если выйдут все, то не выйду я, потому что все и без меня уберут. Другой пример — перевозка грузов в Китае, о котором я узнал в замечательной книге Стивена Ландсбурга «Экономист на диване».
100-150 лет назад в Китае был распространен способ перевозки грузов: все складывалось в большой кузов, который тащили семь человек. Заказчики платили, если груз доставлялся вовремя. Представьте, что вы — один из этих шести. Вы можете прилагать усилия, и тянуть изо всех сил, и если все будут так делать, груз доедет вовремя.
Если кто-нибудь один так делать не будет, все тоже доедут вовремя. Каждый думает: «Если все остальные тянут как следует, зачем это делать мне, а если все остальные тянут не со всей силы, то я ничего не смогу изменить». В итоге, со временем доставки все было очень плохо, и сами грузчики нашли выход: они стали нанимать седьмого и платить ему деньги за то, чтобы он стегал лентяев плетью. Само наличие такого человека заставляло всех работать изо всех сил, потому что иначе все попадали в плохое равновесие, из которого никому в отдельности с выгодой не выйти.
Такой же пример можно наблюдать в природе. Дерево, растущее в саду, отличается от того, что растет в лесу, своей кроной. В первом случае она окружает весь ствол, во втором — находится только вверху. В лесу это является равновесием по Нэшу. Если бы все деревья договорились и выросли одинаково, они бы поровну распределили количество фотонов, и всем было бы лучше.
Но никому в отдельности так делать невыгодно. Поэтому каждое дерево хочет вырасти немного выше окружающих.
Сommitment device
Во многих ситуациях одному из участников игры может понадобиться инструмент, который убедит остальных, что тот не блефует. Он называется commitment device. Например, закон некоторых стран запрещает платить выкуп похитителям людей, чтобы снизить мотивацию преступников. Однако это законодательство часто не работает.
Если вашего родственника захватили, и у вас есть возможность спасти его, обойдя закон, вы это сделаете. Представим ситуацию, что закон можно обойти, но родственники оказались бедными и выкуп им платить нечем. У преступника в этой ситуации два пути: отпустить или убить жертву. Убивать он не любит, но тюрьму он не любит больше.
Отпущенный пострадавший, в свою очередь, может либо дать показания, чтобы похититель был наказан, либо молчать. Самый лучший исход для преступника: отпустить жертву, которая его не сдаст. Жертва же хочет быть отпущенной и дать показания.
Равновесие здесь в том, что террорист не хочет быть пойманным, а значит, жертва погибает. Но это не равновесие по Парето, потому что существует вариант, при котором всем лучше — жертва на свободе хранит молчание. Но для этого надо сделать так, чтобы молчать ей было выгодно. Где-то я прочитал вариант, когда она может попросить террориста устроить эротическую фотосессию.
Если преступника посадят, его подельники выложат фотографии в интернет. Теперь, если похититель останется на свободе — это плохо, но фотографии в открытом доступе — еще хуже, поэтому получается равновесие. Для жертвы это способ остаться в живых.

Другие примеры игр:

Раз уж мы говорим об экономике, рассмотрим экономический пример. В модели Бертрана два магазина продают один и тот же товар, покупая его у производителя по одной цене. Если цены в магазинах одинаковы, то примерно одинакова и их прибыль, ведь тогда покупатели выбирают магазин случайно. Единственное равновесие по Нэшу здесь — продавать товар по себестоимости.
Но магазины хотят зарабатывать. Поэтому если один поставит цену 10 рублей, второй снизит ее на копейку, увеличив тем самым свою выручку вдвое, так как к нему уйдут все покупатели. Поэтому участникам рынка выгодно снижать цены, распределяя тем самым прибыль между собой.
Разъезд на узкой дороге
Рассмотрим примеры выбора между двумя возможными равновесиями. Представьте, что Петя и Маша едут навстречу друг другу по узкой дороге. Дорога настолько узкая, что им обоим нужно съехать на обочину. Если они решат повернуть налево или направо от себя, они просто разъедутся. Если же один повернет направо, а другой налево от себя, или наоборот, случится авария.
Как выбрать, куда съехать? Чтобы помогать искать равновесие в подобных играх, существуют, например, правила дорожного движения. В России каждому нужно повернуть направо.
В забаве Chiken, когда два человека едут на большой скорости навстречу друг другу, тоже есть два равновесия. Если оба сворачивают на обочину, возникает ситуация, которая называется Chiken out, если оба не сворачивают, то погибают в страшной аварии. Если я знаю, что мой соперник едет прямо, мне выгодно съехать, чтобы выжить.
Если я знаю, что мой соперник съедет, то мне выгодно ехать прямо, чтобы после получить 100 долларов. Сложно предсказать, что случится на самом деле, однако, у каждого из игроков есть свой метод выиграть. Представьте, что я закрепил руль так, что его нельзя повернуть, и показал это своему сопернику. Зная, что у меня нет выбора, соперник отскочит.
Иногда бывает очень сложно перейти из одного равновесия в другое, даже если оно означает пользу для всех. Раскладка QWERTY была создана, чтобы замедлить скорость печати. Поскольку если бы все печатали слишком быстро, головки печатной машинки, которые бьют по бумаге, цеплялись бы друг за друга.
Поэтому Кристофер Шоулз разместил часто стоящие рядом буквы на максимально далеком расстоянии. Если вы зайдете в настройки клавиатуры на своем компьютере, вы сможете выбрать там раскладку Dvorak и печатать гораздо быстрее, так как сейчас нет проблемы аналоговых печатных машин. Дворак рассчитывал, что мир перейдет на его клавиатуру, но мы по-прежнему живем с QWERTY.
Конечно, если бы мы перешли на раскладку Дворака, будущее поколение было бы нам благодарно. Все мы приложили бы усилия и переучились, в результате вышло бы равновесие, в котором все печатают быстро. Сейчас мы тоже в равновесии — в плохом. Но никому не выгодно быть единственным, кто переучится, потому что за любым компьютером, кроме личного, работать будет неудобно.
Источник: theoryandpractice.ru
